Section 6 4 Objectives Interpret the chisquare distribution

Section 6. 4 Objectives • Interpret the chi-square distribution and use a chisquare distribution table • Use the chi-square distribution to construct a confidence interval for the variance and standard deviation Larson/Farber 4 th ed 1

The Chi-Square Distribution • The point estimate for 2 is s 2 • The point estimate for is s • s 2 is the most unbiased estimate for 2 Estimate Population with Sample Parameter… Statistic Variance: σ2 s 2 Standard deviation: σ s Larson/Farber 4 th ed 2

The Chi-Square Distribution • You can use the chi-square distribution to construct a confidence interval for the variance and standard deviation. • If the random variable x has a normal distribution, then the distribution of forms a chi-square distribution for samples of any size n > 1. Larson/Farber 4 th ed 3

Properties of The Chi-Square Distribution 1. All chi-square values χ2 are greater than or equal to zero. 2. The chi-square distribution is a family of curves, each determined by the degrees of freedom. To form a confidence interval for 2, use the χ2 -distribution with degrees of freedom equal to one less than the sample size. • d. f. = n – 1 Degrees of freedom 3. The area under each curve of the chi-square distribution equals one. Larson/Farber 4 th ed 4

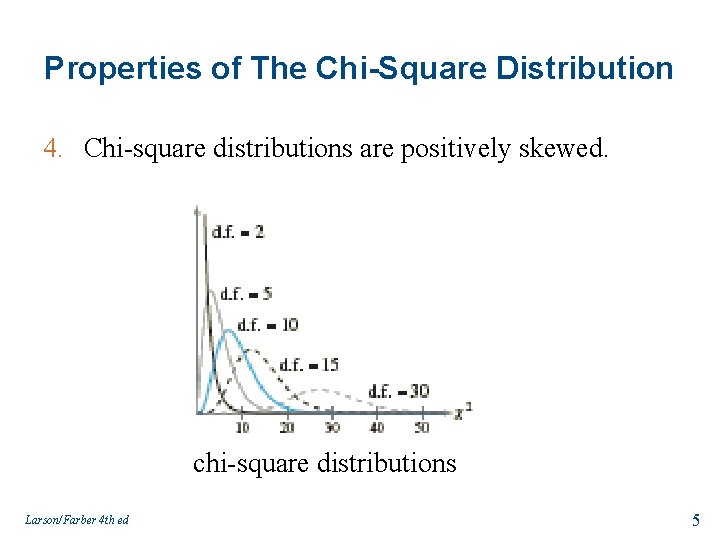
Properties of The Chi-Square Distribution 4. Chi-square distributions are positively skewed. chi-square distributions Larson/Farber 4 th ed 5

Critical Values for χ2 • There are two critical values for each level of confidence. • The value χ2 R represents the right-tail critical value • The value χ2 L represents the left-tail critical value. c The area between the left and right critical values is c. χ2 Larson/Farber 4 th ed 6

Example: Finding Critical Values for χ2 Find the critical values and for a 90% confidence interval when the sample size is 20. Solution: • d. f. = n – 1 = 20 – 1 = 19 d. f. • Each area in the table represents the region under the chi-square curve to the right of the critical value. • Area to the right of χ2 R = • Area to the right of χ2 L = Larson/Farber 4 th ed 7

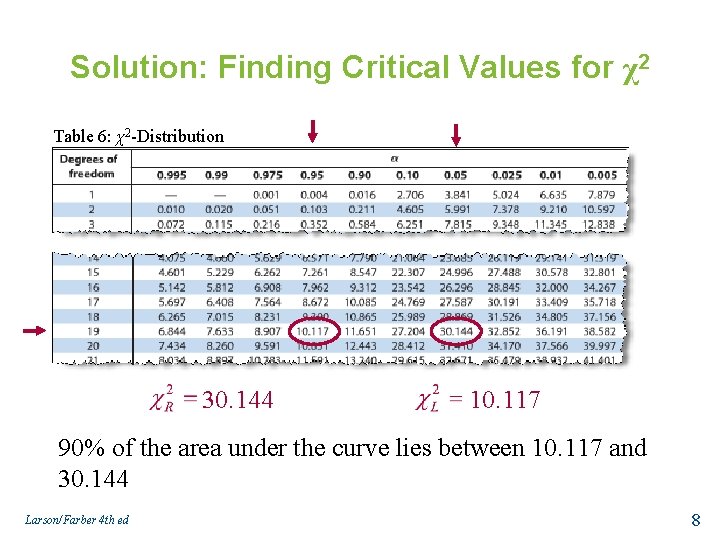
Solution: Finding Critical Values for χ2 Table 6: χ2 -Distribution 30. 144 10. 117 90% of the area under the curve lies between 10. 117 and 30. 144 Larson/Farber 4 th ed 8

Confidence Intervals for 2 and Confidence Interval for 2: • Confidence Interval for : • • The probability that the confidence intervals contain σ2 or σ is c. Larson/Farber 4 th ed 9

Confidence Intervals for 2 and In Words In Symbols 1. Verify that the population has a normal distribution. 2. Identify the sample statistic n and the degrees of freedom. d. f. = n – 1 3. Find the point estimate s 2. 4. Find the critical value χ2 R and χ2 L that correspond to the given level of confidence c. Larson/Farber 4 th ed Use Table 6 in Appendix B 10

Confidence Intervals for 2 and In Words In Symbols 5. Find the left and right endpoints and form the confidence interval for the population variance. 6. Find the confidence interval for the population standard deviation by taking the square root of each endpoint. Larson/Farber 4 th ed 11

Example: Constructing a Confidence Interval You randomly select and weigh 30 samples of an allergy medicine. The sample standard deviation is 1. 20 milligrams. Assuming the weights are normally distributed, construct 99% confidence intervals for the population variance and standard deviation. Solution: • d. f. = n – 1 = 30 – 1 = 29 d. f. Larson/Farber 4 th ed 12

Solution: Constructing a Confidence Interval • Area to the right of χ2 R = • Area to the right of χ2 L = • The critical values are χ2 R = 52. 336 and χ2 L = 13. 121 Larson/Farber 4 th ed 13

Solution: Constructing a Confidence Interval for 2: Left endpoint: Right endpoint: 0. 80 < σ2 < 3. 18 With 99% confidence you can say that the population variance is between 0. 80 and 3. 18 milligrams. Larson/Farber 4 th ed 14

Solution: Constructing a Confidence Interval for : 0. 89 < σ < 1. 78 With 99% confidence you can say that the population standard deviation is between 0. 89 and 1. 78 milligrams. Larson/Farber 4 th ed 15

Section 6. 4 Summary • Interpreted the chi-square distribution and used a chisquare distribution table • Used the chi-square distribution to construct a confidence interval for the variance and standard deviation Larson/Farber 4 th ed 16