Section 6 4 Graph Coloring Color the counties

Section 6. 4 Graph Coloring

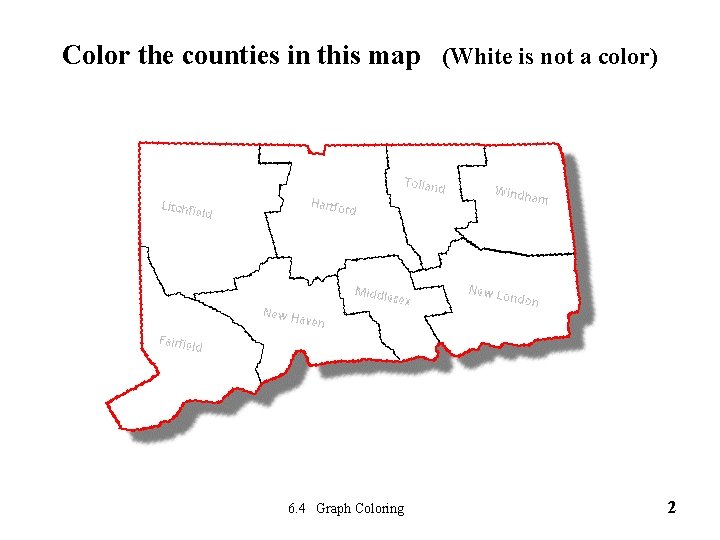
Color the counties in this map (White is not a color) 6. 4 Graph Coloring 2

How many colors did you use? 1. 2 -3 2. 4 -5 3. 6 -7 4. 8 -9 6. 4 Graph Coloring 3

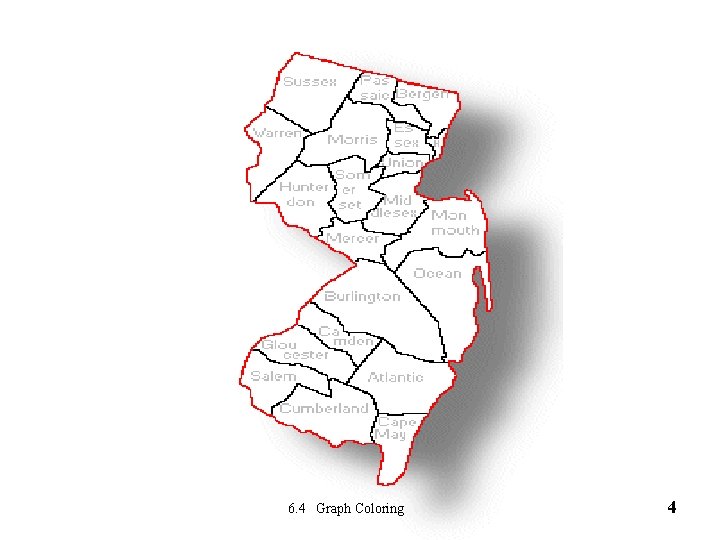
6. 4 Graph Coloring 4

How many colors did you use? 1. 2 -3 2. 4 -5 3. 6 -7 4. 8 -9 6. 4 Graph Coloring 5

Two rules for coloring 1. 2. 6. 4 Graph Coloring 6

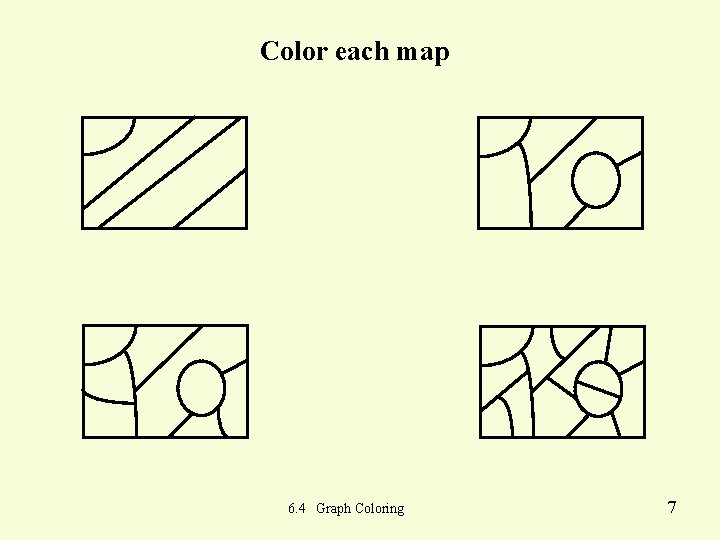
Color each map 6. 4 Graph Coloring 7

Draw a map that requires 5 colors Example 5 colors 6. 4 Graph Coloring 8

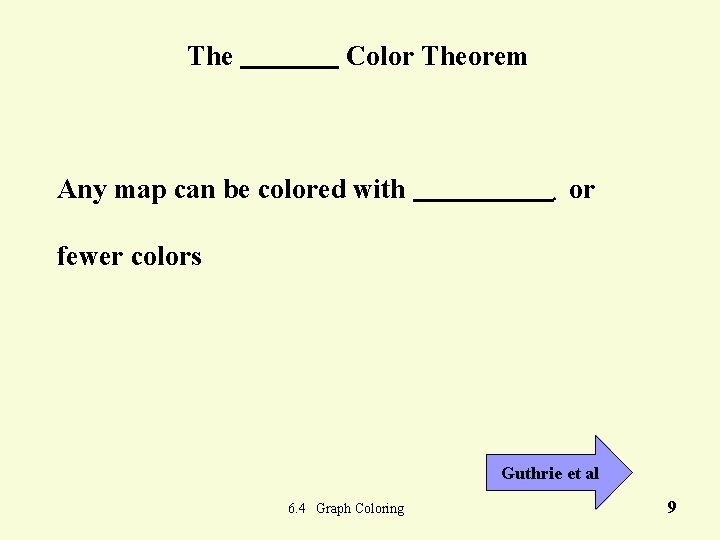
The Color Theorem Any map can be colored with . or fewer colors Guthrie et al 6. 4 Graph Coloring 9

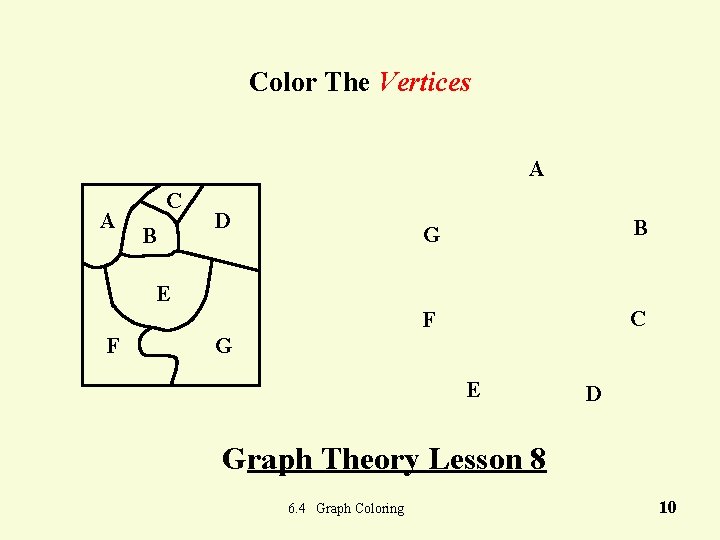
Color The Vertices A A C B D G B F C E F G E D Graph Theory Lesson 8 6. 4 Graph Coloring 10

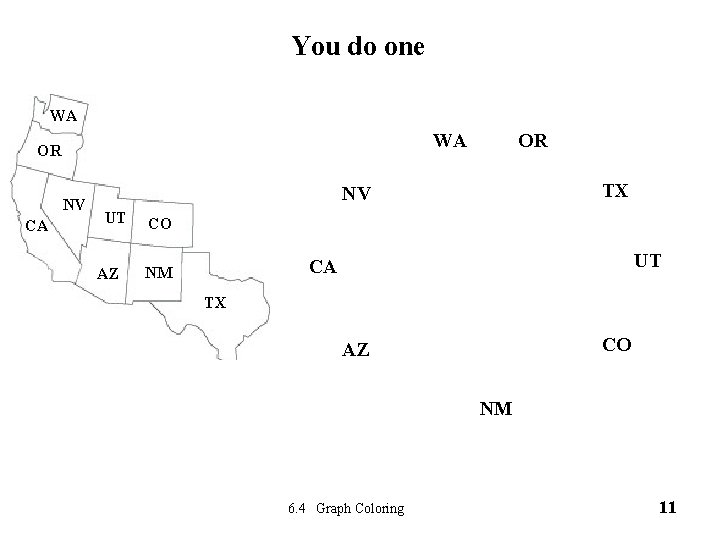
You do one WA WA OR NV CA OR TX NV UT AZ CO UT CA NM TX CO AZ NM 6. 4 Graph Coloring 11

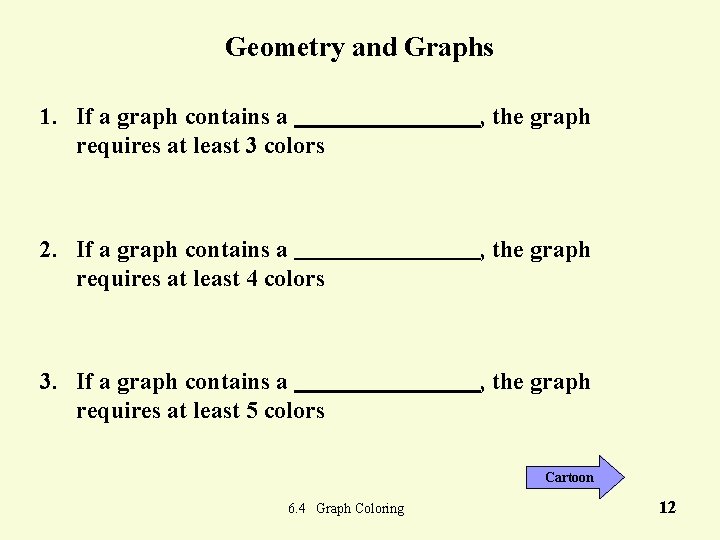
Geometry and Graphs 1. If a graph contains a requires at least 3 colors , the graph 2. If a graph contains a requires at least 4 colors , the graph 3. If a graph contains a requires at least 5 colors , the graph Cartoon 6. 4 Graph Coloring 12

“Student Council Committees” A student council consists of 7 students a, b, c, d, e, f, g. Each student belongs to several of 6 committees These committees meet weekly for an hour at the same time (noon). All members must be present before business can be conducted. There are lots of meeting rooms available. Executive (E) = {a, b, c} Ways/Means (W) = {b, d, e} Finance (F) = {a, b, d} By-Laws (B) = {a, c, g} Social (S) = {e, f} Recruiting (R) = {c, e, f, g} What is the fewest number of days required to schedule all 6 committees? 6. 4 Graph Coloring 13

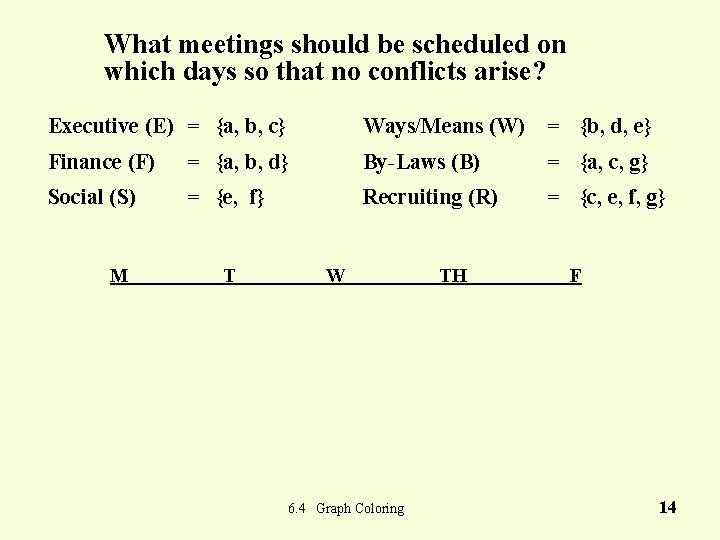
What meetings should be scheduled on which days so that no conflicts arise? Executive (E) = {a, b, c} Ways/Means (W) = {b, d, e} Finance (F) = {a, b, d} By-Laws (B) = {a, c, g} Social (S) = {e, f} Recruiting (R) = {c, e, f, g} M T W 6. 4 Graph Coloring TH F 14

Executive (E) Finance (F) Social (S) Ways and Means (W) By-Laws (B) Recruiting (R) Sports (SP) Coordinating (C) Academic (A) Newsletter (N) Outreach (O) Fund-raising (FR) = = = 6. 4 Graph Coloring {a, b, c, f, h} {a, b, d, e} {c, e, f} {b, d, e, g, h} {a, c, g} {c, e, f, g} {a, b, c} {a, b, d, g} {b, e, f, h} {b, d, e, h} {a, c, g} {a, c, e, f, g} 15

Executive (E) Finance (F) Social (S) Ways/Means (W) By-Laws (B) Recruiting (R) 4 -Step Algorithm 1. Vertices = Parties = = = {a, b, c} {a, b, d} {e, f} {b, d, e} {a, c, g} {c, e, f, g} . 2. Edges join parties Exec 3. Color the vertices 4. # colors = # days required Recru Fin M By-Laws Soc T W Th F WM 6. 4 Graph Coloring 16

“Final Exams” A: English, Science, Politics D: English, French, Art B: Science, Politics, Philosophy E: Politics, Art, Philosophy C: Math, Philosophy, Art F: Math, Science, Music A school has six graduating seniors: Adams (A), Black (B), Courtois (C), D’Amico (D), Epstein (E), and Flaherty (F) You must prepare a final exam schedule for these students. Students can take only one exam each day What is the fewest number of days required to schedule all 8 exams? 6. 4 Graph Coloring 17

A: English, Science, Politics D: English, French, Art B: Science, Politics, Philosophy E: Politics, Art, Philosophy C: Math, Philosophy, Art F: Math, Science, Music 6. 4 Graph Coloring 18

How many days are required? 1. 3 2. 4 3. 5 4. 6 6. 4 Graph Coloring 19

A: English, Science, Politics D: English, French, Art B: Science, Politics, Philosophy E: Politics, Art, Philosophy C: Math, Philosophy, Art F: Math, Science, Music G: Music, Philosophy H: Science, French 6. 4 Graph Coloring 20

If G is added how many days are required? 1. 3 2. 4 3. 5 4. 6 6. 4 Graph Coloring 21

If both G and H are added how many days are required? 1. 3 2. 4 3. 5 4. 6 6. 4 Graph Coloring 22

“Desperate Housewives” You owe party invitations to several sets of friends: Browns, Caldwells, Fortins, Grandes, Martens, Nevins, and Princes. Three nights (Thursday, Friday, and Saturday) are available However, you know that it would make for a happier time for all if several of the couples were not to come on the same night Can you schedule all of your friends on the three nights? 6. 4 Graph Coloring 23

• Nevins don’t get along with Browns or Fortins • Martins usually argue politics with Nevins • Princes and Grandes are in-laws whose kids are fighting • Prince just sued Brown and Fortin • Caldwell and Martin are spiteful business competitors • One of the Browns is having an affair with one of the Caldwells • Fortin’s owe the Grandes a considerable amount of money 6. 4 Graph Coloring 24

How many nights are necessary? • • Nevins don’t get along with Browns or Fortins Martins usually argue politics with Nevins Princes and Grandes are in-laws whose kids are fighting Prince just sued Brown and Fortin Caldwell and Martin are spiteful business competitors One of the Browns is having an affair with one of the Caldwells Fortin’s owe the Grandes a considerable amount of money 1. 2 2. 3 3. 4 6. 4 Graph Coloring 25

One more complication Nevins don’t get along with Browns or Fortins Martins usually argue politics with Nevins Princes and Grandes are in-laws whose kids are fighting Prince just sued Brown and Fortin Caldwell and Martin are spiteful business competitors One of the Browns is having an affair with one of the Caldwells Fortin’s owe the Grandes a considerable amount of money Browns had a long-standing feud with both the Fortins and the Grandes? . 1. 2 2. 3 3. 4 4. 5 6. 4 Graph Coloring 26

End of 6. 4 Graph Coloring

Francis Guthrie 1831 -1899 6. 4 Graph Coloring 28

Wolfgang Haken and Kenneth Appel 6. 4 Graph Coloring 29

Scheduling Conflicts Oh, What to do? What to Dooooo? 6. 4 Graph Coloring 30

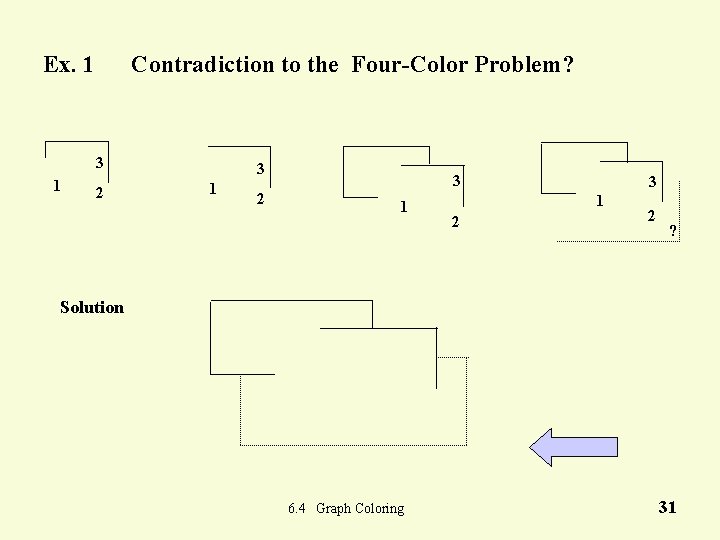
Ex. 1 Contradiction to the Four-Color Problem? 3 1 2 2 ? Solution 6. 4 Graph Coloring 31

Meta - Material 6. 4 Graph Coloring