Section 6 3 Understanding Linear and Nonlinear Functions

Section 6. 3: Understanding Linear and Nonlinear Functions Objectives: Students will be able to Identify Linear Functions Identify Nonlinear Functions from graphs Describe and Sketch Functions

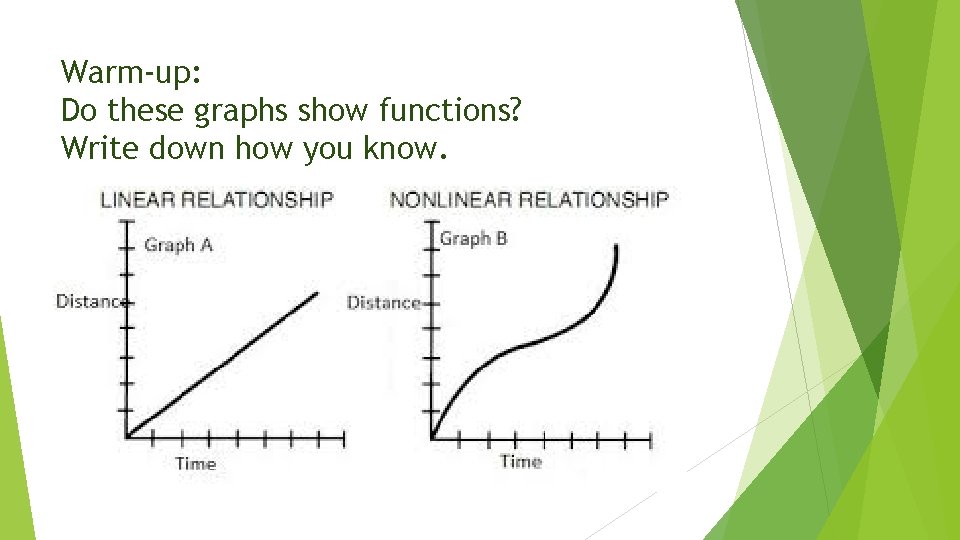
Warm-up: Do these graphs show functions? Write down how you know.

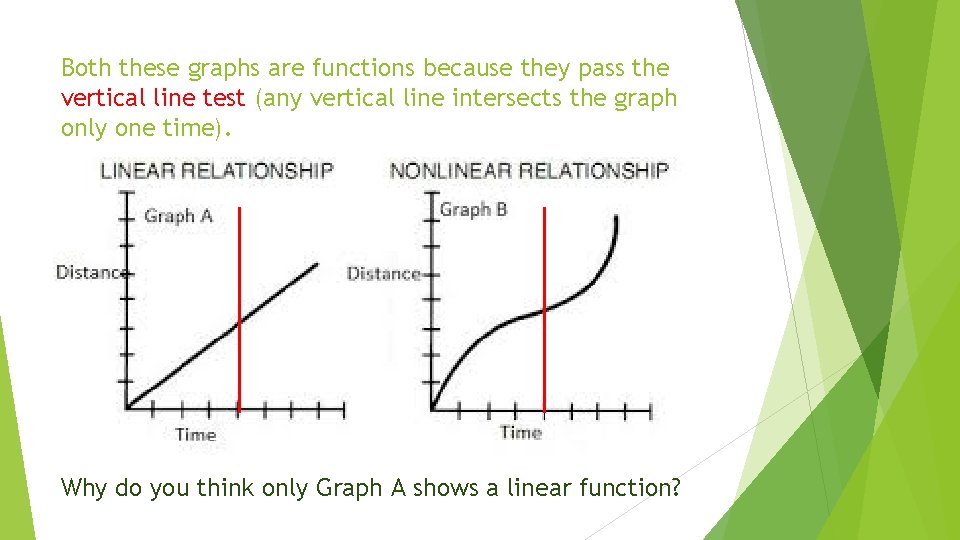
Both these graphs are functions because they pass the vertical line test (any vertical line intersects the graph only one time). Why do you think only Graph A shows a linear function?

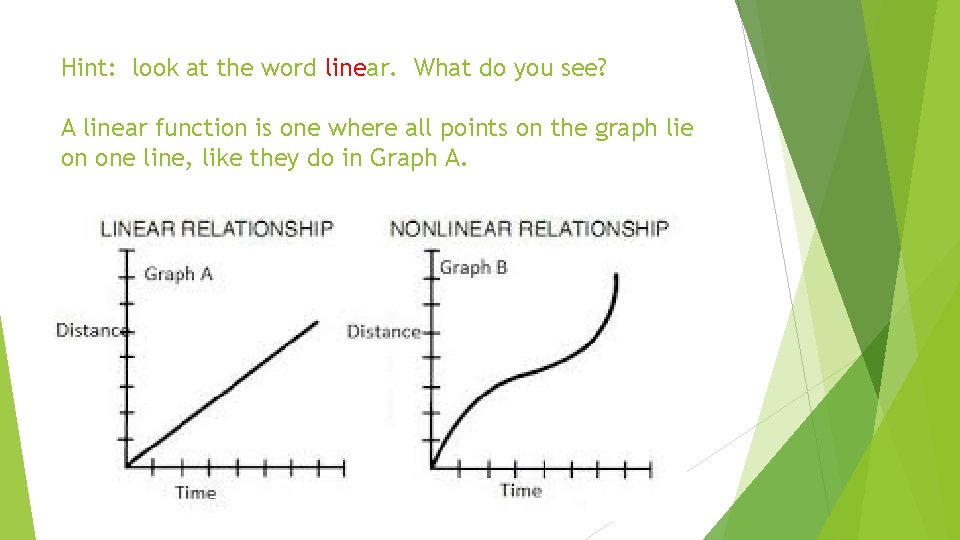
Hint: look at the word linear. What do you see? A linear function is one where all points on the graph lie on one line, like they do in Graph A.

Review from last lesson: Determining linear functions from their tables Tell if this function is linear OR nonlinear. The table shows the increase in size of a hot air balloon as it is filled up with air. Tell whether the relation between the volume of air, v liters, and the time to fill the balloon, t minutes, is a linear function. Step 1: Copy the table. Fill in the x- and y- changes.

Warm-up: Tell if this function is linear OR nonlinear. Check your results: Step 2: Use the x- and y-changes to write three fractions.

Warm-up: Tell if this function is linear OR nonlinear. Step 2: Use the x- and y-changes to write three fractions. The fractions are: 20/1, and 40/2. Step 3: Does this function show a constant change?

Tell if this function is linear OR nonlinear. The fractions are: 20/1, and 40/2. Step 3: Does this function show a constant change? Since all fractions reduce to 20, there is a constant rate of change. Step 4: Is this a linear function?

A linear function shows a constant rate of change. When all fractions reduce to the same number, this is a constant rate of change and is a linear function. A nonlinear function shows varying rates of change. When all fractions ARE NOT equal, this function has a varying rate of change and is NOT a linear function. Our function is a linear function because it shows a constant rate of change.

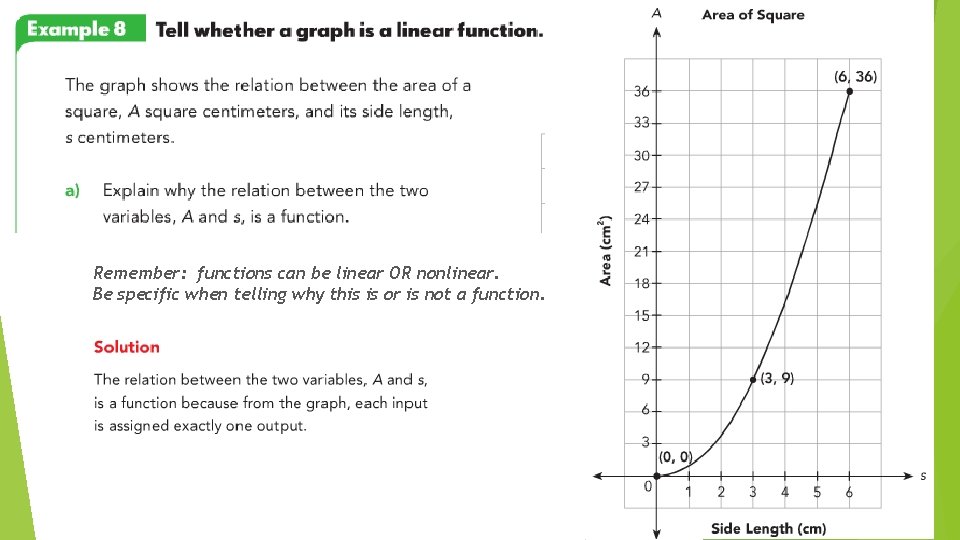
Remember: functions can be linear OR nonlinear. Be specific when telling why this is or is not a function.

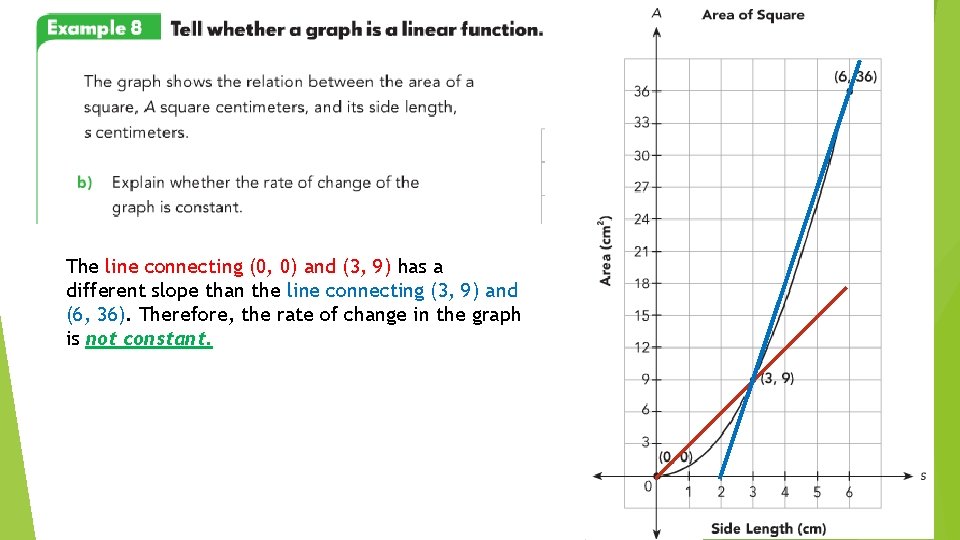
The line connecting (0, 0) and (3, 9) has a different slope than the line connecting (3, 9) and (6, 36). Therefore, the rate of change in the graph is not constant.

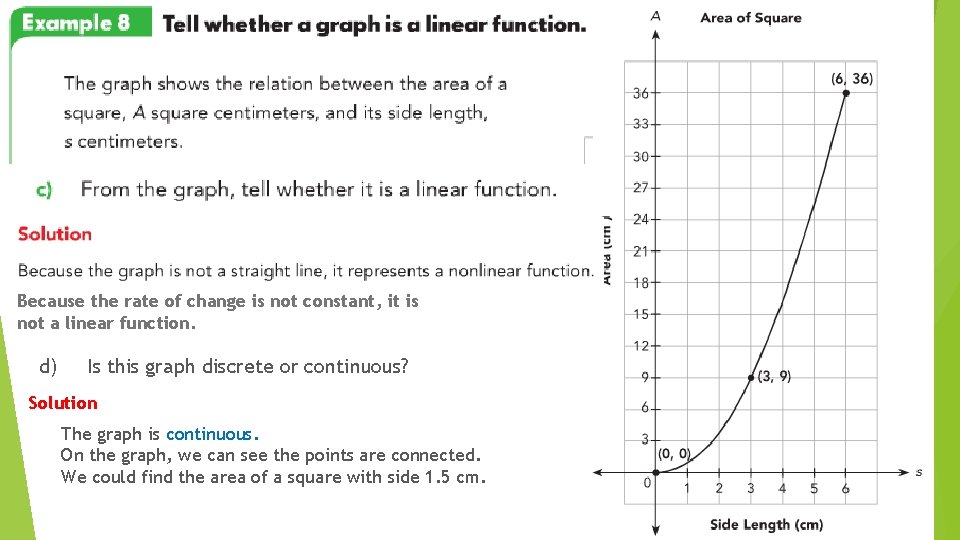
Because the rate of change is not constant, it is not a linear function. d) Is this graph discrete or continuous? Solution The graph is continuous. On the graph, we can see the points are connected. We could find the area of a square with side 1. 5 cm.

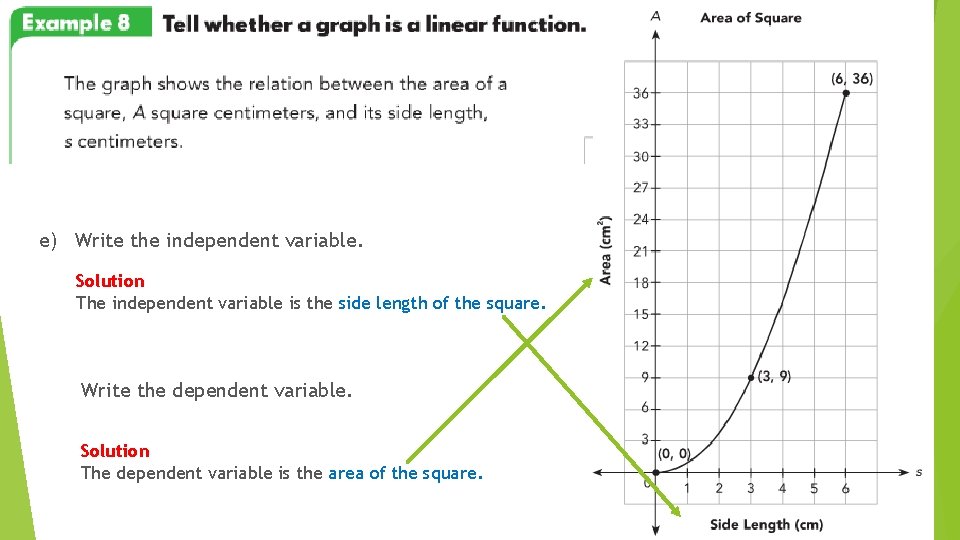
e) Write the independent variable. Solution The independent variable is the side length of the square. Write the dependent variable. Solution The dependent variable is the area of the square.

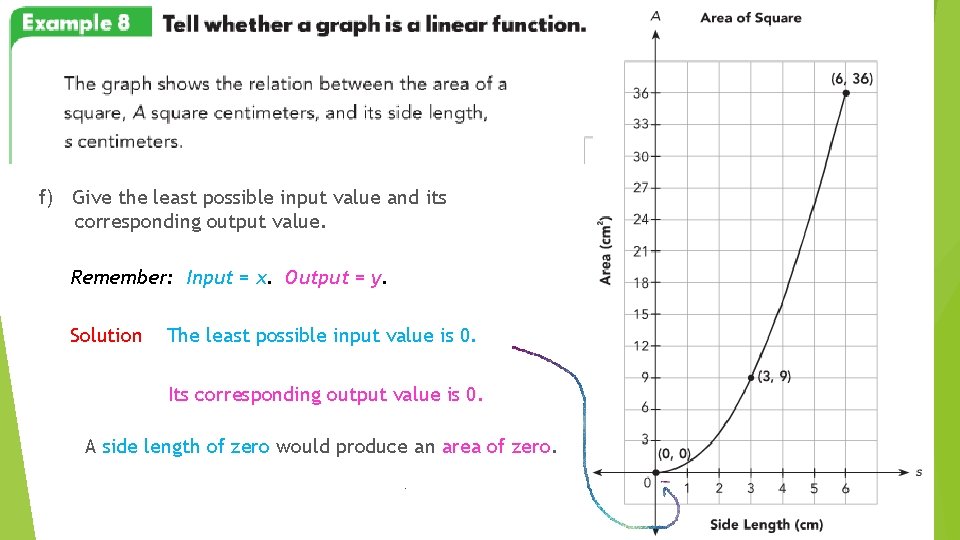
f) Give the least possible input value and its corresponding output value. Remember: Input = x. Output = y. Solution The least possible input value is 0. Its corresponding output value is 0. A side length of zero would produce an area of zero.

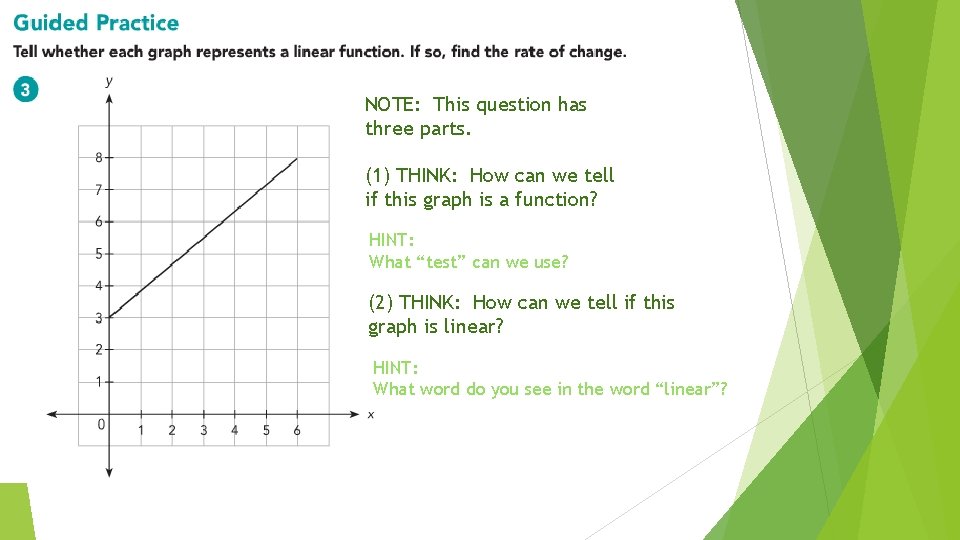
NOTE: This question has three parts. (1) THINK: How can we tell if this graph is a function? HINT: What “test” can we use? (2) THINK: How can we tell if this graph is linear? HINT: What word do you see in the word “linear”?

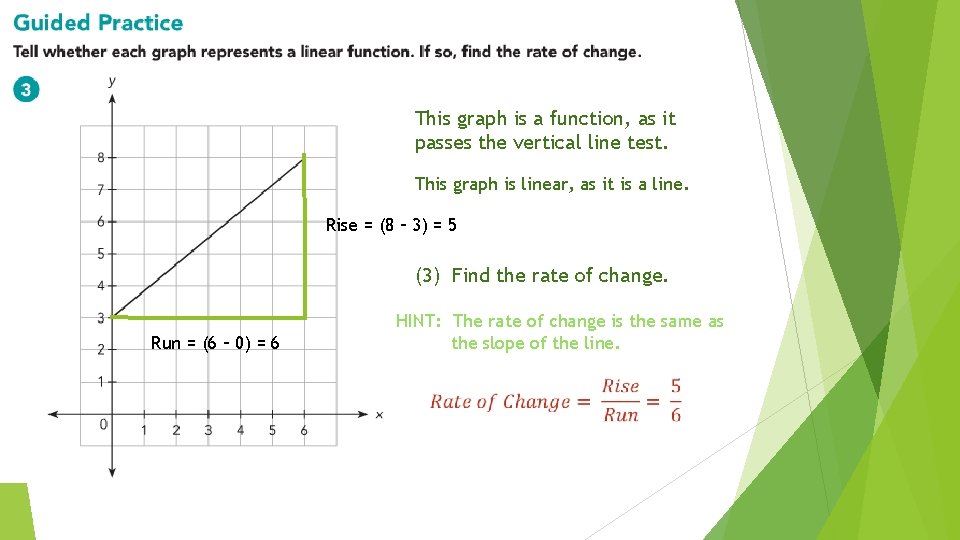
This graph is a function, as it passes the vertical line test. This graph is linear, as it is a line. Rise = (8 – 3) = 5 (3) Find the rate of change. Run = (6 – 0) = 6 HINT: The rate of change is the same as the slope of the line.

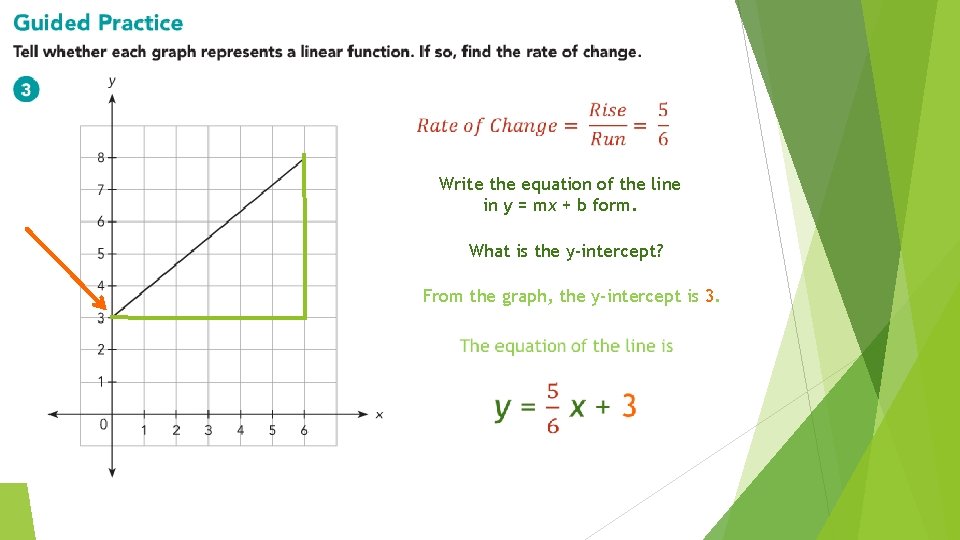
Write the equation of the line in y = mx + b form. What is the y-intercept? From the graph, the y-intercept is 3.

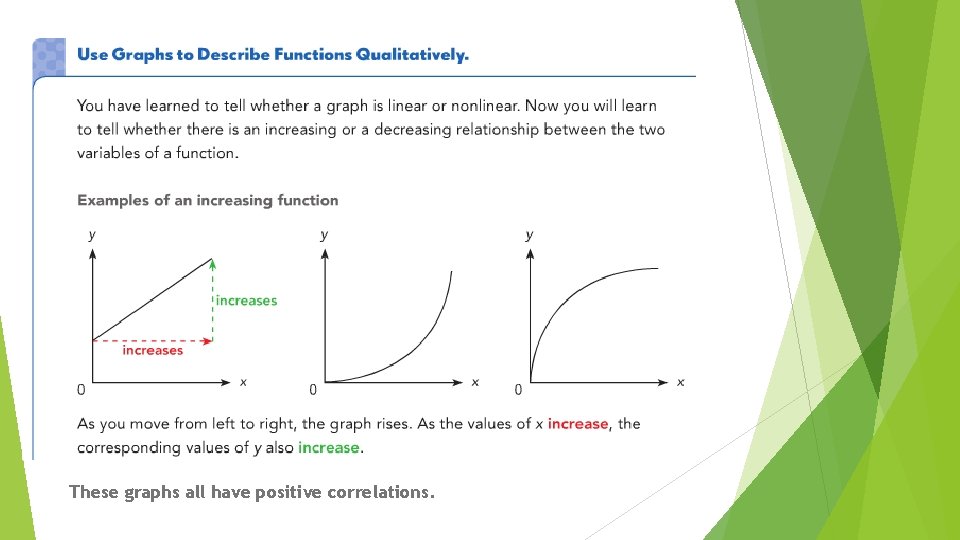
These graphs all have positive correlations.

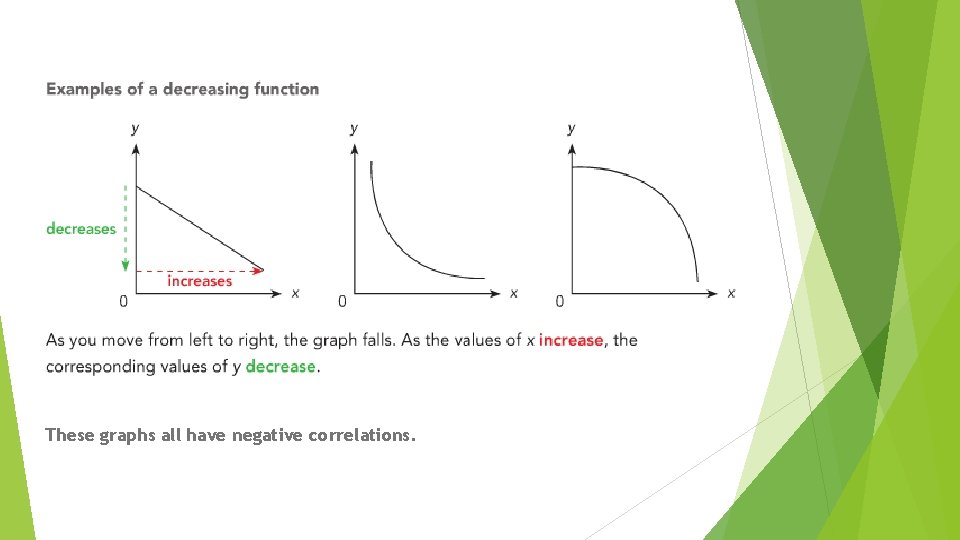
These graphs all have negative correlations.

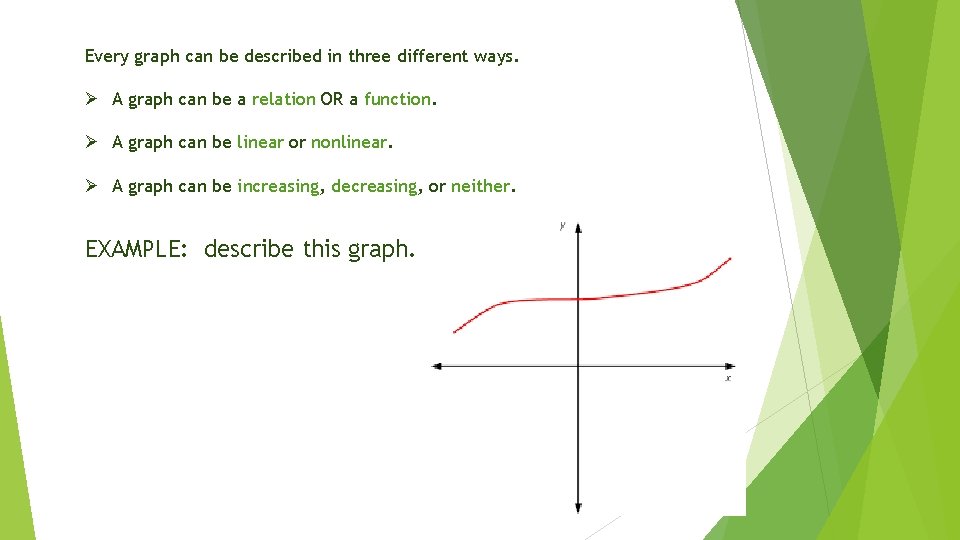
Summary: STUDY THESE PROPERTIES OF GRAPHS! Every graph can be described in three different ways. Ø A graph can be a relation OR a function. Ø A graph can be linear or nonlinear. Ø A graph can be increasing, decreasing, or neither.

Every graph can be described in three different ways. Ø A graph can be a relation OR a function. Ø A graph can be linear or nonlinear. Ø A graph can be increasing, decreasing, or neither. EXAMPLE: describe this graph.

Every graph can be described in three different ways. Ø A graph can be a relation OR a function. THINK: does it pass the vertical line test? Ø A graph can be linear or nonlinear. THINK: is it a straight line? Ø A graph can be increasing or decreasing. THINK: does it go up or down? Write three answers on your paper.

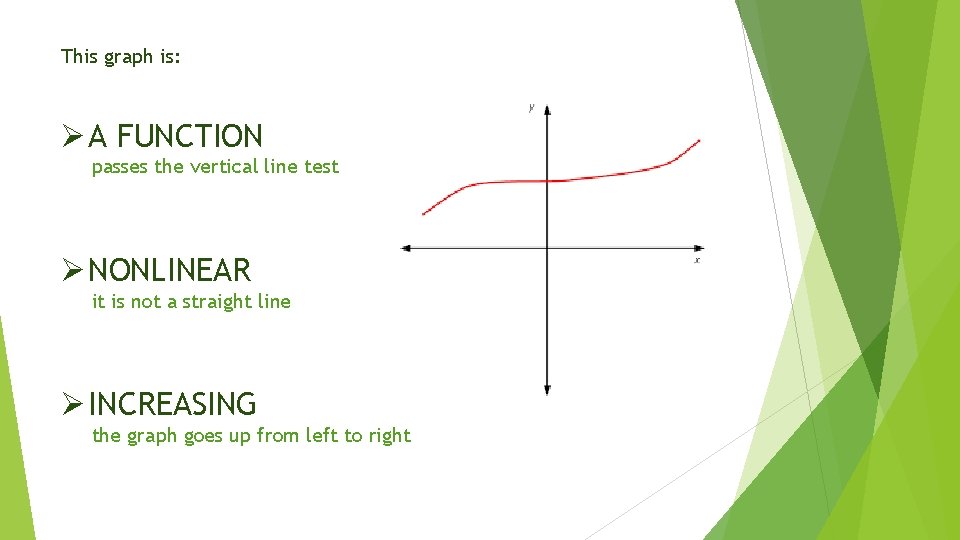
This graph is: Ø A FUNCTION passes the vertical line test Ø NONLINEAR it is not a straight line Ø INCREASING the graph goes up from left to right

Your assignment is due by 3 pm tomorrow (Tuesday). Please try to submit through Microsoft Teams. If you cannot, please send me one e-mail with all the assignments attached. 1. Book page 276 (5 -10) 2. Worksheet 6. 3 – use page 277 (11 -13) in your book. For #12, you can just sketch a rough graph to get an idea of what it looks like. On the back of the worksheet, you will find a function review.