SECTION 6 3 GENERAL PROBABILITY RULES Joint Events

SECTION 6. 3 GENERAL PROBABILITY RULES Joint Events Conditional Probability HIV Testing

SUMMARY OF PROBABILITY RULES The probability of any event “A” is: The probability of all the events in a sample space is 1: Independent Events: Complement Events: Disjoint Events: (Mutually Exclusive Events) Empty Intersection

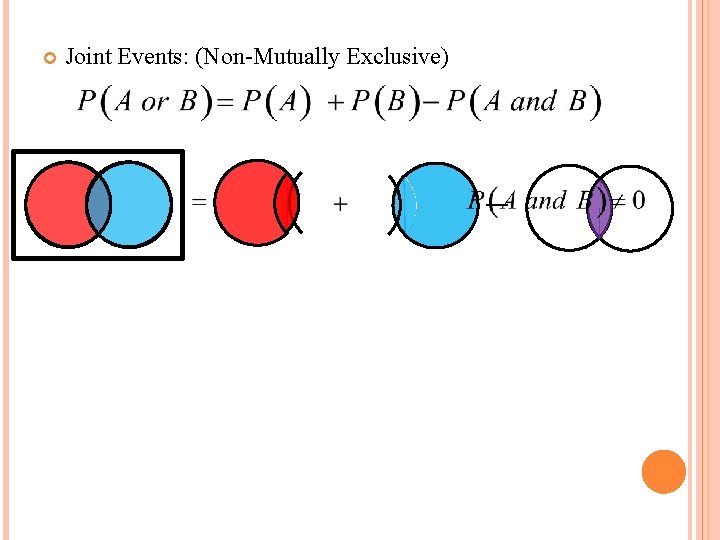
Joint Events: (Non-Mutually Exclusive)

EX: ADDITION RULE –JOINT EVENTS The accompanying table represents the blood groups and RH types of 100 people. Based on the table what is the probability a person will have group B blood or be RH Positive? The commonly-used terms Rh factor, Rh positive and Rh negative refer to the D antigen only. Besides its role in blood transfusion, the Rh blood group system, in particular the strongest D antigen, is a relevant cause of the hemolytic disease of the newborn or erythroblastosis fetalis for which prevention is key. An antigen is a substance or molecule that when introduced into the body triggers the production of an antibody by the immune system which will then kill or neutralize the antigen that is recognized as a foreign and potentially harmful invader.

Ex: A study of credit card fraud was conducted by Master Card International, and the table below is based on the results. Based on the table, what is the probability that fraud resulted from a stolen card or a mail/phone order ? The events are all mutually exclusive. The intersection is empty

EXAMPLE –PAGE 364, #6. 48 Ex: Consolidated builders has bid on two large construction projects. The company president believes that the probability of winning the first contract (event A) is 0. 6, that the probability of winning the second (event B) is 0. 5, and that the joint probability of winning both jobs (event {A and B}) is 0. 3. What is the probability of event {A or B} that Consolidated will win at least one of the jobs?

CONDITIONAL PROBABILITY P(B|A) – the probability that event ‘B’ will occur, GIVEN that event ‘A’ has already occurred The probability that “B’ will occur Given that event ‘A’ has occurred “given” symbol The probability of event “B” may or may not be affected by the occurrence of event “A” Event “B” is not affected if events “A” & “B” are independent Event “B” is affected if events “A” & “B” are dependent Therefore, most conditional probabilities in this section have to do with “Dependent Events” or “Joint Events” © Copyright all rights reserved to Homework depot: www. bcmath. ca

CONDITIONAL PROBABILITY To find the probability of event B given the event A, we restrict our attention to the outcomes in A. We then find in what fraction of those outcomes B also occurred. What is the probability that both Events A and B will occur Within the probability that event A has occurred If the events of “A” and “B” are independent, then their conditions will not affect each other.

INDEPENDENT VS DEPENDENT EVENTS: Ex: Two marbles are drawn from a jar Event A: 1 st marble is red Event B: 2 nd marble is green Find P(B|A) i) There is replacement (Independent) Given that the 1 st draw is a red marble We replaced the red marble back into the jar The probability that the 2 nd marble is green is not affected, because the two events are independent ii) There is NO replacement (Dependent) When given that the 1 st draw is a red marble, the number of red in the jar is decreased The probability of getting a green marble in the 2 nd draw is greater Therefore, if events A & B are independent then: © Copyright all rights reserved to Homework depot: www. bcmath. ca

FIND P(B|A) FOR EACH OF THE FOLLOWING EXPERIMENTS i) A dice is rolled twice (A) – 1 st roll is even (B) – 2 nd roll is odd Events ‘A’ and ‘B’ are independent ii)(A) – 1 st roll is 5 (B) – the sum of the two rolls is 8 Events ‘A’ and ‘B’ are Dependent If the first roll is a 5, then the second roll has to be a ‘ 3’ iii)(A) – the sum is even List out all the possible even sums: (B) – 2 nd roll is even Events ‘A’ and ‘B’ are Dependent © Copyright all rights reserved to Homework depot: www. bcmath. ca

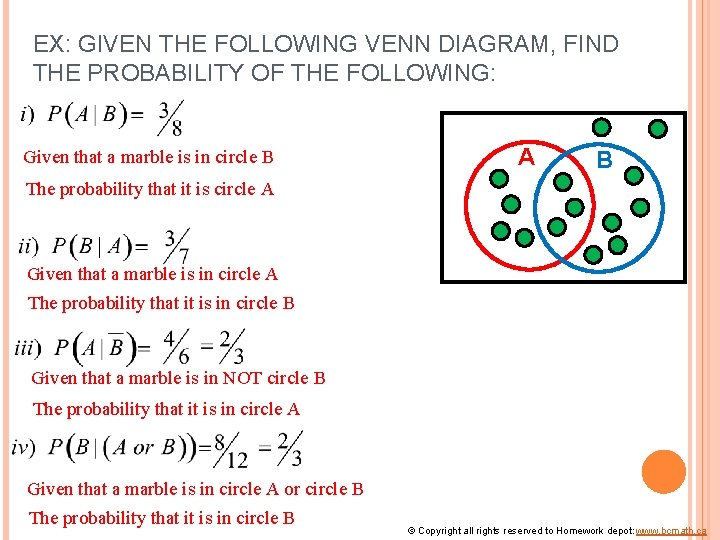
EX: GIVEN THE FOLLOWING VENN DIAGRAM, FIND THE PROBABILITY OF THE FOLLOWING: Given that a marble is in circle B A B The probability that it is circle A Given that a marble is in circle A The probability that it is in circle B Given that a marble is in NOT circle B The probability that it is in circle A Given that a marble is in circle A or circle B The probability that it is in circle B © Copyright all rights reserved to Homework depot: www. bcmath. ca

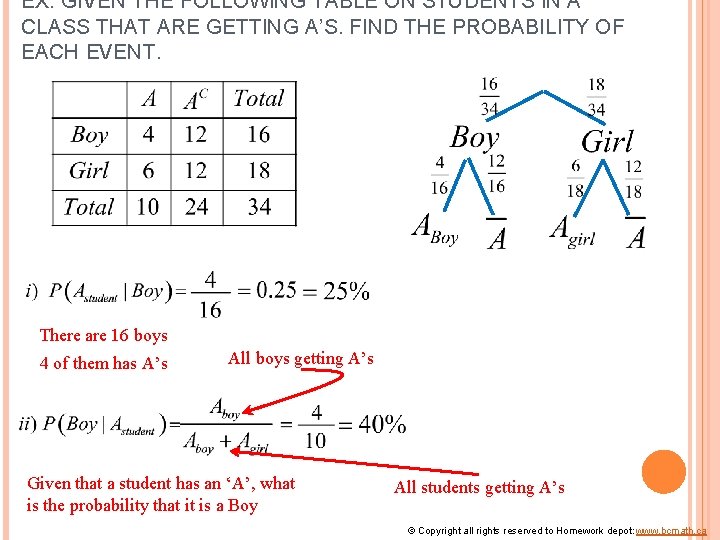
EX: GIVEN THE FOLLOWING TABLE ON STUDENTS IN A CLASS THAT ARE GETTING A’S. FIND THE PROBABILITY OF EACH EVENT. There are 16 boys 4 of them has A’s All boys getting A’s Given that a student has an ‘A’, what is the probability that it is a Boy All students getting A’s © Copyright all rights reserved to Homework depot: www. bcmath. ca

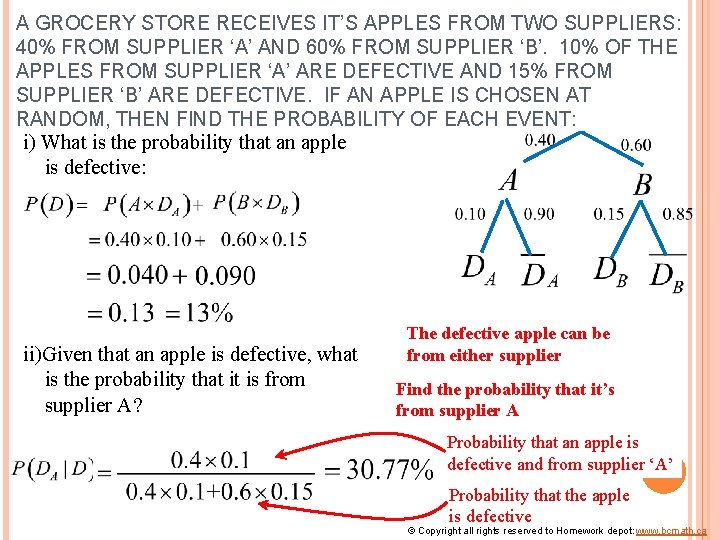
A GROCERY STORE RECEIVES IT’S APPLES FROM TWO SUPPLIERS: 40% FROM SUPPLIER ‘A’ AND 60% FROM SUPPLIER ‘B’. 10% OF THE APPLES FROM SUPPLIER ‘A’ ARE DEFECTIVE AND 15% FROM SUPPLIER ‘B’ ARE DEFECTIVE. IF AN APPLE IS CHOSEN AT RANDOM, THEN FIND THE PROBABILITY OF EACH EVENT: i) What is the probability that an apple is defective: ii)Given that an apple is defective, what is the probability that it is from supplier A? The defective apple can be from either supplier Find the probability that it’s from supplier A Probability that an apple is defective and from supplier ‘A’ Probability that the apple is defective © Copyright all rights reserved to Homework depot: www. bcmath. ca

Ex: Police report that 78% of drivers are given a breath test, 36% a blood test, and 22% both tests. a) Are giving a DWI suspect a blood test and a breath test mutually exclusive? b) Are giving the two tests independent? Soln: State the events we’re interest in. Let A = {suspect is given a breath test}. Let B = {suspect is given a blood test}. a) If the two events are mutually exclusive then: Since the intersection is not empty, then they are not M. E. b) If the two events are independent then: Not equal, so not independent

EXAMPLE –PAGE 370, #6. 56 Ex: Choose an employed person at random. Let “A” be the event that the person chosen is a women and “B” the event that the person holds a managerial or professional job. Government data tell us that P(A) = 0. 46 and the probability of managerial and professional jobs among women is P(B|A) = 0. 32. Find the probability that a randomly chosen employed person is a women holding a managerial or professional position.

EXAMPLE –PAGE 378, #6. 64 Ex: Enzyme immuno-assay (EIA) tests are used to screen blood specimens for the presence of antibodies to HIV, the virus that causes AIDS. These antibodies indicate the presence of the virus. The test is 99. 85% accurate but is not always correct. Here approximate probabilities of positive and negative EIA outcomes when the blood tested does and does not actually contain antibodies to HIV. It is estimated that 1% of the population carries antibodies to HIV in their blood.

Note: Someone who is HIV positive may be unaware of their disease. When the EIA test is performed, we don’t actually know their medical condition A) When someone is tested positive for HIV, what is the probability that he/she is actually HIV positive? B) When someone is tested positive for HIV, what is the probability that he/she is actually HIV negative? C) When someone is tested negative for HIV, what is the probability that he/she is actually HIV positive? D) Many medical professionals would claim that this test is 99. 85% accurate, but what does this percentage actually imply?

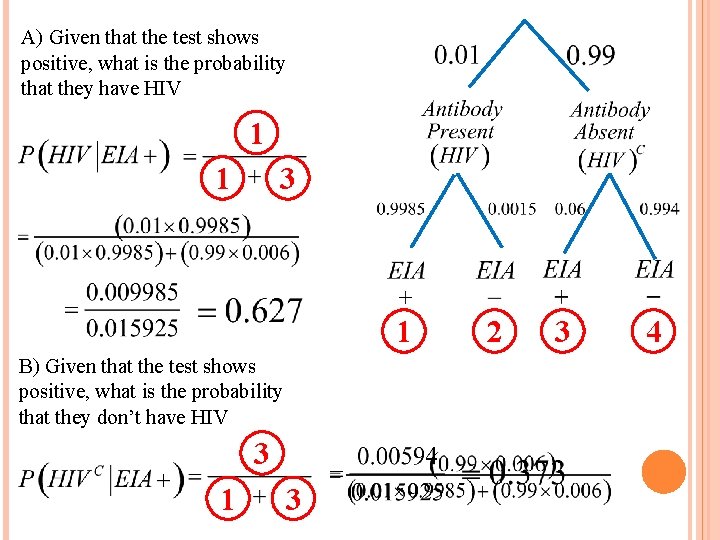
A) Given that the test shows positive, what is the probability that they have HIV 1 1 3 1 B) Given that the test shows positive, what is the probability that they don’t have HIV 3 1 3 2 3 4

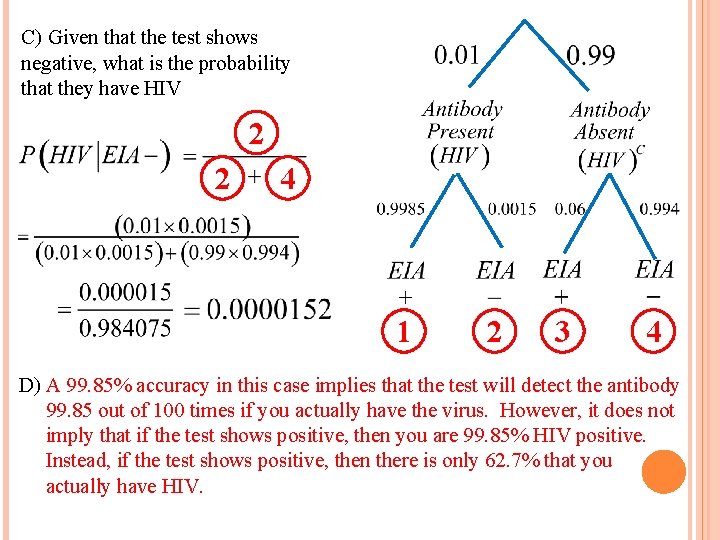
C) Given that the test shows negative, what is the probability that they have HIV 2 2 4 1 2 3 4 D) A 99. 85% accuracy in this case implies that the test will detect the antibody 99. 85 out of 100 times if you actually have the virus. However, it does not imply that if the test shows positive, then you are 99. 85% HIV positive. Instead, if the test shows positive, then there is only 62. 7% that you actually have HIV.