Section 6 3 Applications of Normal Distribution Learning

Section 6. 3 Applications of Normal Distribution

Learning Targets This section presents methods for working with normal distributions that are not standard. That is, the mean is not 0 or the standard deviation is not 1, or both. The key concept is that we can use a simple conversion that allows us to standardize any normal distribution so that the same methods of the previous section can be used.

�In Section 6. 2 we considered the standard normal distribution. However, this is an ideal situation and not always relatable to the real world. �What do we use when we have a real life situation with some mean and some standard deviation? Let’s Get REAL

�Air Midwest 5481 crashed in Charlotte, North Carolina. All of the 21 people on board were killed. �What was the reason for this crash? What Do The Following Have in Common?

�A water taxi sank in Baltimore’s Inner Harbor. Among the 25 people on board, 5 died and 16 were injured. �What was the reason for this crash? What Do The Following Have in Common?

� 20 passengers were killed when the Ethan Allen tour boat capsized on New York’s Lake George. �What was the reason for this crash? What Do The Following Have in Common?

� First, they all were preventable. � Each were working off an old standard – that the mean weight of a person is 140 lbs. � This was no longer the case and based on passenger loads, the mean weight of the passengers was so heavy it resulted in the crashes. � Normal distributions are essential for understanding what to expect. � In particular, this area of study is called Ergonomics – the study of how people fit into their environment. Real World Uses For Normal Distributions

�To convert values to standard z-scores use the formula below then following the procedures for working with all normal distributions discussed in Section 6. 2. Round z scores to 2 decimal places How To Convert Z-Scores

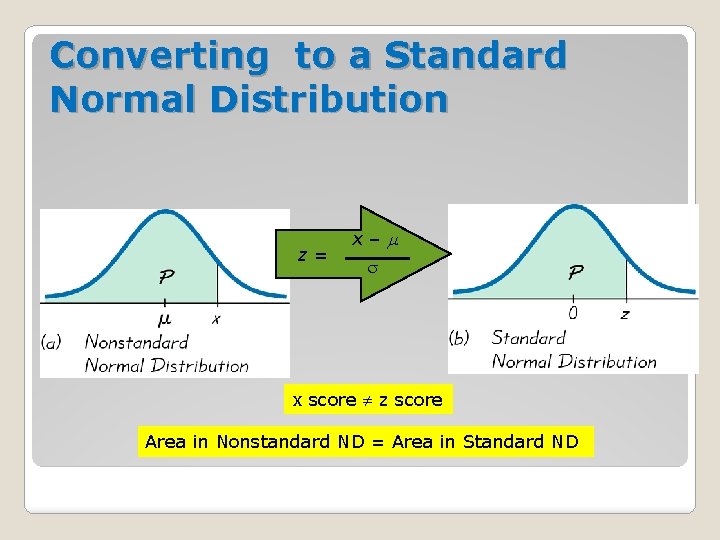
Converting to a Standard Normal Distribution z= x– x score z score Area in Nonstandard ND = Area in Standard ND

Method for Finding Nonstandard Normal Distribution Areas or Probabilities (When being asked to find an area or probability you will use the same method) In the following notations, x represents a non-standardized individual value. • P(a < x < b) : denotes the probability that the z score is between a and b. To find this probability in your calculator, type: normalcdf(a, b, µ, σ) • P(x > a) : denotes the probability that the z score is greater than a. To find this probability in your calculator, type: normalcdf(a, 9999, µ, σ) • P(x < a) : denotes the probability that the z score is less than a. To find this probability in your calculator, type: normalcdf(– 9999, a, µ, σ)

Example – Weights of Water Taxi Passengers In the Chapter Problem, we noted that the safe load for a water taxi was found to be 3500 pounds. We also noted that the mean weight of a passenger was assumed to be 140 pounds. Assume the worst case that all passengers are men. Assume also that the weights of the men are normally distributed with a mean of 172 pounds and standard deviation of 29 pounds. If one man is randomly selected, what is the probability he weighs less than 174 pounds?

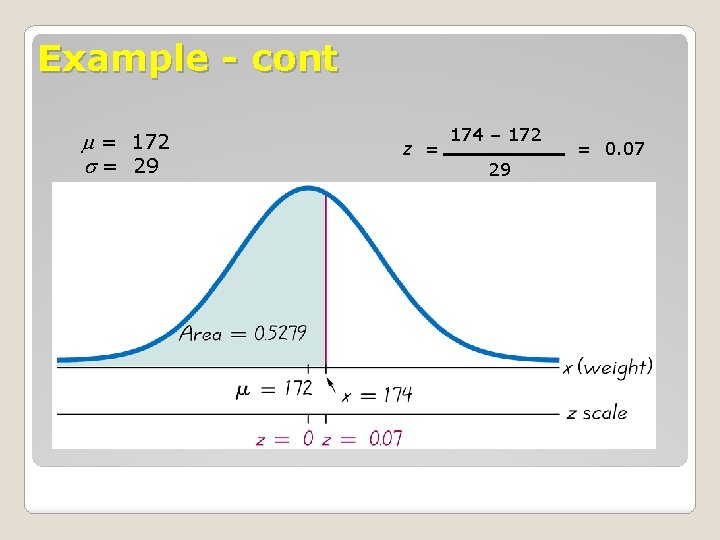
Example - cont = 172 = 29 z = 174 – 172 29 = 0. 07

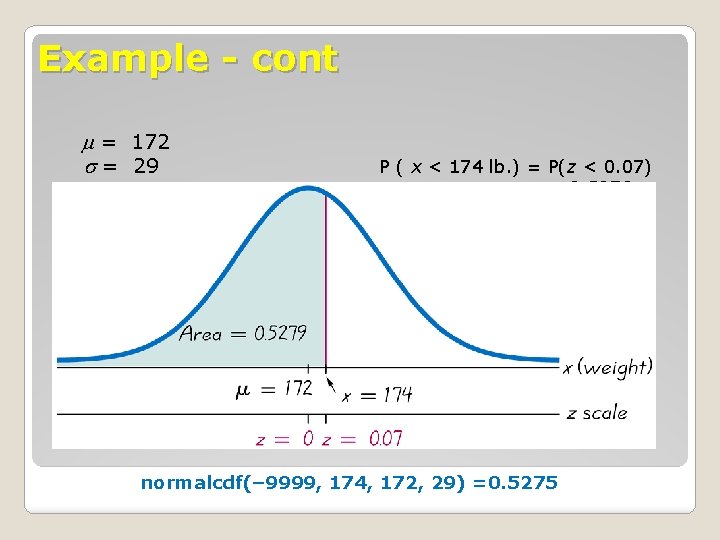
Example - cont = 172 = 29 P ( x < 174 lb. ) = P(z < 0. 07) = 0. 5279 normalcdf(– 9999, 174, 172, 29) =0. 5275

Helpful Hints 1. Don’t confuse z scores and areas. z scores are distances along the horizontal scale, but areas are regions under the normal curve. Table A-2 lists z scores in the left column and across the top row, but areas are found in the body of the table. 2. Choose the correct (right/left) side of the graph. 3. A z score must be negative whenever it is located in the left half of the normal distribution. 4. Areas (or probabilities) are positive or zero values, but they are never negative.

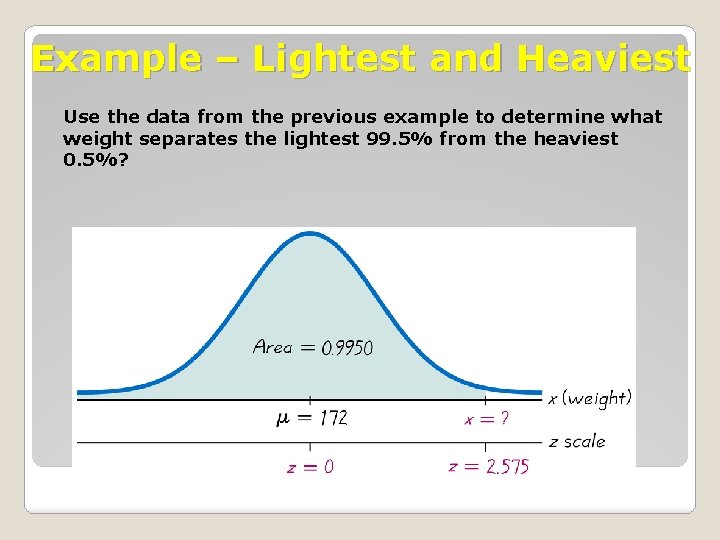
Example – Lightest and Heaviest Use the data from the previous example to determine what weight separates the lightest 99. 5% from the heaviest 0. 5%?

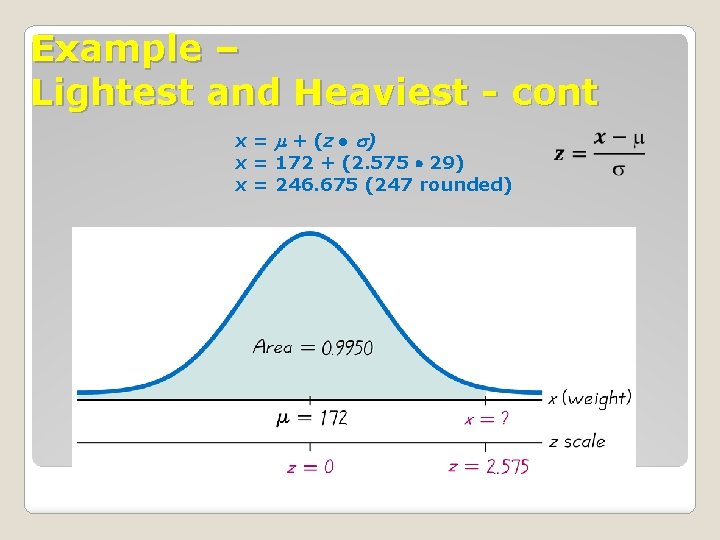
Example – Lightest and Heaviest - cont x = + (z ● ) x = 172 + (2. 575 29) x = 246. 675 (247 rounded)

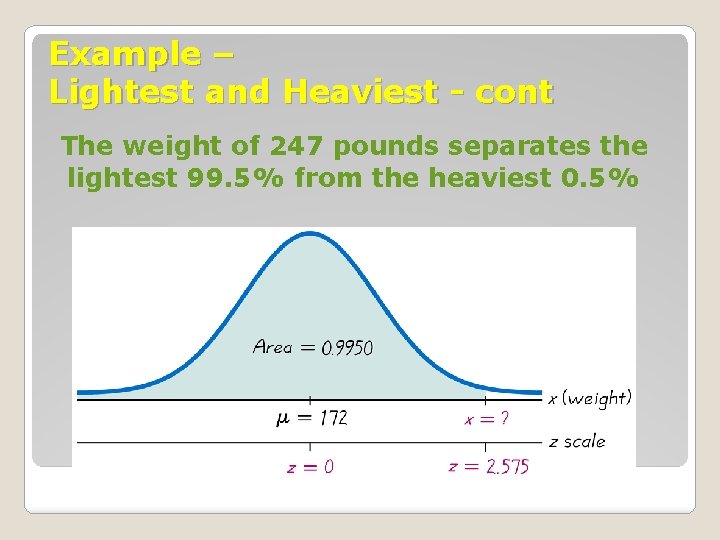
Example – Lightest and Heaviest - cont The weight of 247 pounds separates the lightest 99. 5% from the heaviest 0. 5%

The typical home doorway has a height of 6 ft 8 in. Given that heights of men are normally distributed with a mean of 69 in. and a standard deviation of 2. 8 in. , find the percentage of men who can fit through the standard doorway without bending or bumping their head. 6’ 8” = 80” Will a doorway of height 6 ft 8 in. be sufficient in future years? normalcdf(– 9999, 80, 69, 2. 8) =0. 99995 100% Why Do Doorways Have a Height of 6 ft 8 in. ?

What if we wanted to design a doorway that 95% of men will fit through without bending or bumping their heads. How high should that doorway be assuming heights of men are normally distributed with a mean of 69 in. and a standard deviation of 2. 8 in? inv. Norm(0. 95, 69, 2. 8) =73. 61 74 inch. Designing Doorway Heights

Your Turn: Use the following information to answer the questions that follow: *Men’s heights are normally distributed with mean 69. 0 in. and standard deviation 2. 8 in. *Women’s heights are normally distributed with mean 63. 6 in. and standard deviation 2. 5 in. The Mark VI monorail used at Disney World and the Boeing 757 -200 ER airliner have doors with a height of 72 in. a) What percentage of adult men can fit through the doors without bending? normalcdf(– 9999, 72, 69, 2. 8) = 85. 8%

Your Turn: Use the following information to answer the questions that follow: *Men’s heights are normally distributed with mean 69. 0 in. and standard deviation 2. 8 in. *Women’s heights are normally distributed with mean 63. 6 in. and standard deviation 2. 5 in. The Mark VI monorail used at Disney World and the Boeing 757 -200 ER airliner have doors with a height of 72 in. b) What percentage of adult women can fit through the doors without bending? normalcdf(– 9999, 72, 63. 6, 2. 5) =0. 9996 = 99. 96%

Birth weights in the U. S are normally distributed with a mean of 3420 g and a standard deviation of 495 g. Hospitals require special treatment for babies that are less than 2450 g (unusually light) or more than 4390 g (unusually heavy). What percentage of babies do not require special treatment? normalcdf(2450, 4390, 3420, 495) 95% Birth Weights

Birth weights in the U. S are normally distributed with a mean of 3420 g and a standard deviation of 495 g. The Newport General Hospital wants to redefine the minimum and maximum birth weights that require special treatment because they are unusually low or unusually high. After considering relevant factors, a committee recommends special treatment for birth weights in the lowest 3% and the highest 1%. inv. Norm(0. 03, 3420, 495) 2489 g. inv. Norm(0. 99, 3420, 495) 4572 g. What is the Birth Weights of unusual low and high?

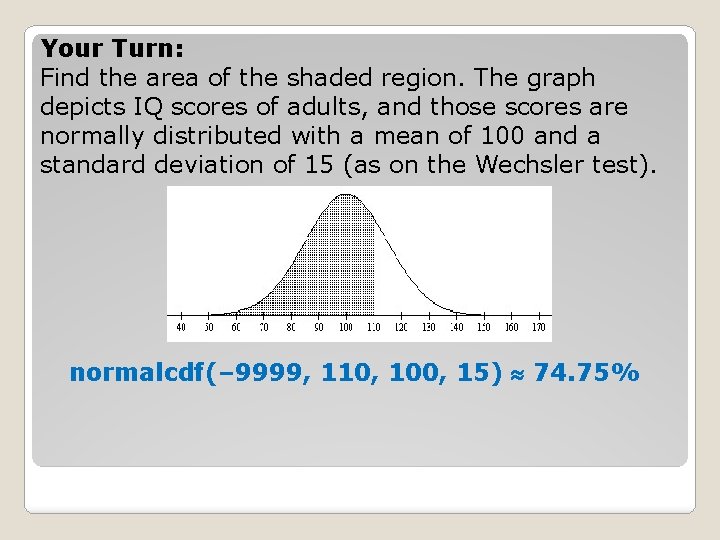
Your Turn: Find the area of the shaded region. The graph depicts IQ scores of adults, and those scores are normally distributed with a mean of 100 and a standard deviation of 15 (as on the Wechsler test). normalcdf(– 9999, 110, 100, 15) 74. 75%

Your Turn: Assume that adults have IQ scores that are normally distributed with a mean of 100 and a standard deviation of 15 (as on the Wechsler test). a) Find P 43 which is the IQ score separating the bottom 43% from the top 57%. inv. Norm(0. 43, 100, 15) = 97. 35 98 b) Find the IQ score separating the top 28% from the others. inv. Norm(1 – 0. 28, 100, 15) =108. 74 109

Example: Use the following information to answer the questions that follow: *Women’s heights are normally distributed with mean 63. 6 in. and standard deviation 2. 5 in. The U. S. Army requires women’s heights to be between 58 in. and 80 in. a) Find the percentage of women meeting the height requirement. normalcdf(58, 80, 63. 6, 2. 5) =98. 75% b) If the U. S. Army changes the height requirements so that all women are eligible except the shortest 1% and tallest 2%, what are the new height requirements? inv. Norm(0. 01, 63. 6, 2. 5) 58 in. inv. Norm(1 – 0. 02, 63. 6, 2. 5) 69 in.

Recap In this section we have discussed: v Non-standard normal distribution. v Converting to a standard normal distribution. v Procedures for finding values using Table A-2 and Formula 6 -2.

�Pg. 272 �#5 -7, 9 -11, #25 OR #26 Practice