Section 6 2 Modeling with Cubic and Quartic

Objectives § Create scatter plots for sets of data (TI 83/84) § Model and apply data with cubic functions § Model and apply data with quartic functions § *Find SSE and average error of the best fit cubic or quartic model (TI 83/84) § Use the best fit model to make predictions (TI 83/84); Identify the type of a prediction (interpolation vs extrapolation) and understand which is more accurate § Compare cubic, quartic, exponential, logarithmic, linear and quadratic models of data; Determine which model is the better model to make predictions Copyright © 2017, 2013, 2010 Pearson Education, Inc. 2

Function Graphs of Cubic Functions End behavior: one end opening up and one end opening down Turning points: 0 or 2 Graphs of Quartic Functions: End behavior: Both ends opening up or both ends opening down Turning points: 1 or 3 Copyright © 2017, 2013, 2010 Pearson Education, Inc. 3

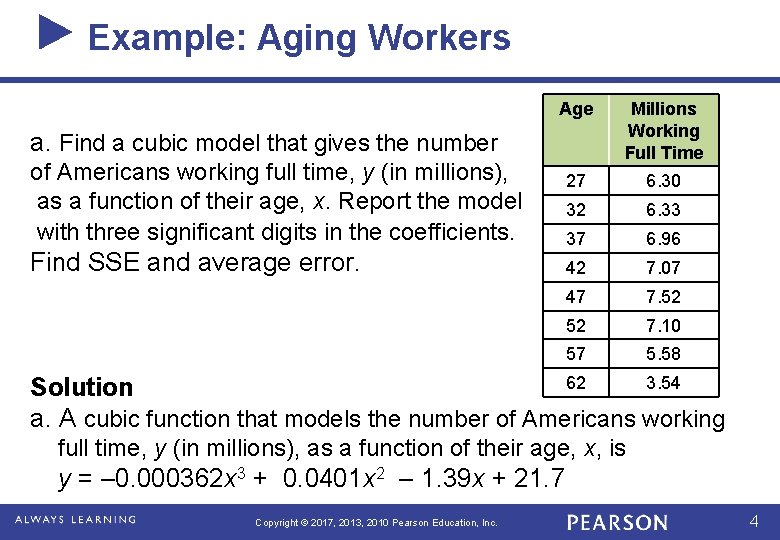
Example: Aging Workers Age Millions Working Full Time 27 6. 30 32 6. 33 37 6. 96 42 7. 07 47 7. 52 52 7. 10 57 5. 58 a. Find a cubic model that gives the number of Americans working full time, y (in millions), as a function of their age, x. Report the model with three significant digits in the coefficients. Find SSE and average error. 62 3. 54 Solution a. A cubic function that models the number of Americans working full time, y (in millions), as a function of their age, x, is y = – 0. 000362 x 3 + 0. 0401 x 2 – 1. 39 x + 21. 7 Copyright © 2017, 2013, 2010 Pearson Education, Inc. 4

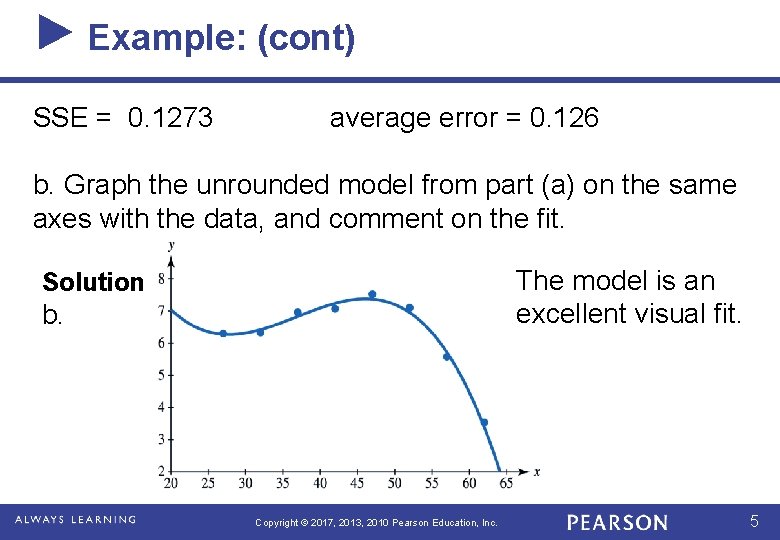
Example: (cont) SSE = 0. 1273 average error = 0. 126 b. Graph the unrounded model from part (a) on the same axes with the data, and comment on the fit. The model is an excellent visual fit. Solution b. Copyright © 2017, 2013, 2010 Pearson Education, Inc. 5

Example: (cont) c. Use the model to estimate the number of Americans working at age 59. Solution c. The number of Americans age 59 who are working is estimated from the model to be y = f (59) ≈ 5 million. Copyright © 2017, 2013, 2010 Pearson Education, Inc. 6

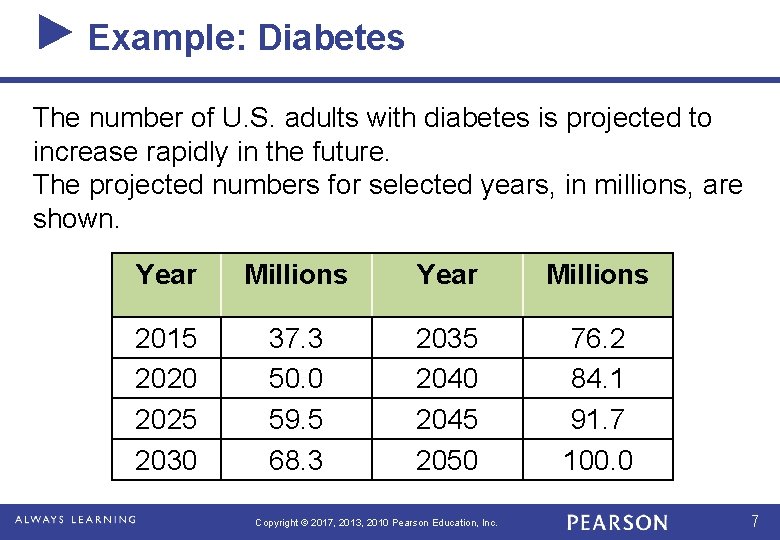
Example: Diabetes The number of U. S. adults with diabetes is projected to increase rapidly in the future. The projected numbers for selected years, in millions, are shown. Year Millions 2015 2020 2025 2030 37. 3 50. 0 59. 5 68. 3 2035 2040 2045 2050 76. 2 84. 1 91. 7 100. 0 Copyright © 2017, 2013, 2010 Pearson Education, Inc. 7

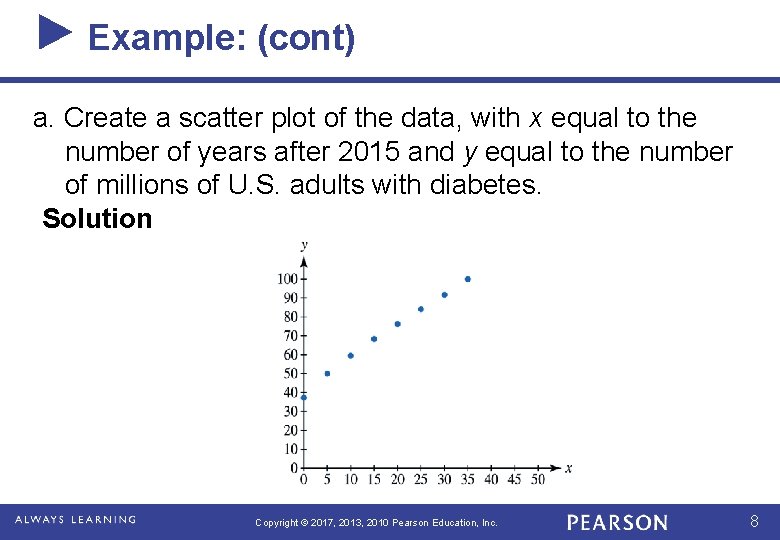
Example: (cont) a. Create a scatter plot of the data, with x equal to the number of years after 2015 and y equal to the number of millions of U. S. adults with diabetes. Solution Copyright © 2017, 2013, 2010 Pearson Education, Inc. 8

Example: (cont) b. Create a linear function that models the data. Report the model with three significant digits. Find SSE and average error. Solution b. The linear function that is the best fit for the data is y = 1. 74 x + 40. 5 SSE = 20. 06 average error = 1. 58 Copyright © 2017, 2013, 2010 Pearson Education, Inc. 9

Example: (cont) c. Create a cubic function that models the data. Report the model with three significant digits. Find SSE and average error. Solution c. The cubic function that is the best fit for the data is y = 0. 000697 x 3 – 0. 0486 x 2 + 2. 64 x + 37. 5 SSE = 0. 373 average error = 0. 216 Copyright © 2017, 2013, 2010 Pearson Education, Inc. 10

Example: (cont) d. Graph the data on the same axes as each model, and determine which is the better fit to the data. Solution d. The graphs of the data on the same axes as the linear function and the cubic function are shown. The fit of the linear function to the data is excellent, but the cubic function is nearly an exact fit to the data, so the cubic function is the better fit. Copyright © 2017, 2013, 2010 Pearson Education, Inc. 11

Example: (cont) e. Determine which of the two models is the better model to predict the number of U. S. adults with diabetes in year 2024 and year 2070, respectively? Explain. Solution: Linear model: 2024 56. 13 2070 135. 99 Cubic model: 57. 78 151. 37 The better model to predict the number of U. S. adults with diabetes in 2024 is cubic model since it is closer to the number projected for 2025 and it has a smaller SSE, and the better model to predict the number of U. S. adults with diabetes in 2070 is linear since the prediction by the cubic model seems to be too large. Copyright © 2017, 2013, 2010 Pearson Education, Inc. 12

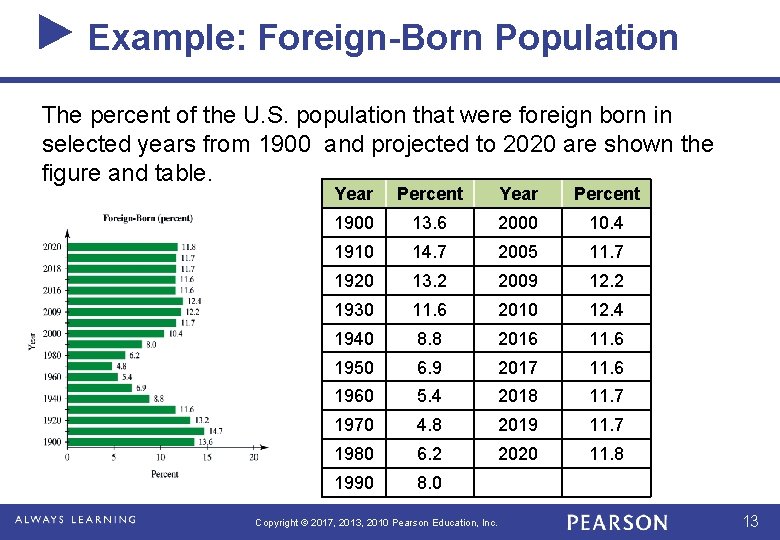
Example: Foreign-Born Population The percent of the U. S. population that were foreign born in selected years from 1900 and projected to 2020 are shown the figure and table. Year Percent 1900 13. 6 2000 10. 4 1910 14. 7 2005 11. 7 1920 13. 2 2009 12. 2 1930 11. 6 2010 12. 4 1940 8. 8 2016 11. 6 1950 6. 9 2017 11. 6 1960 5. 4 2018 11. 7 1970 4. 8 2019 11. 7 1980 6. 2 2020 11. 8 1990 8. 0 Copyright © 2017, 2013, 2010 Pearson Education, Inc. 13

Example: Foreign-Born Population a. Create a scatter plot for the data, using the number of years after 1900 as the input x and the percent as the output y. b. Find a cubic function to model the data and graph the function on the same axes with the data points. Report the model by rounding coefficients to seven decimal places. c. Find a quartic function to model the data and graph the function on the same axes with the data points. Report the model by rounding coefficients to seven decimal places. d. Find SSE and average error for each model. Determine which model is the better model to predict the U. S. population that were foreign born in year 2060. Explain. Copyright © 2017, 2013, 2010 Pearson Education, Inc. 14

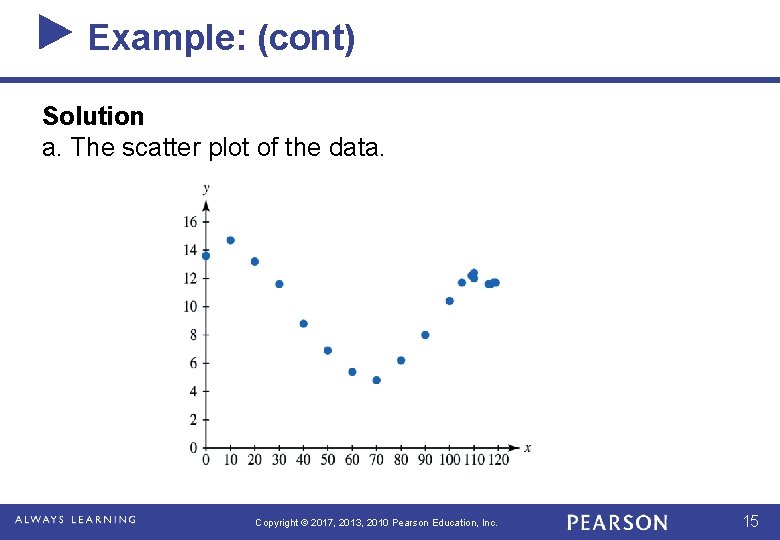
Example: (cont) Solution a. The scatter plot of the data. Copyright © 2017, 2013,

Example: (cont) Solution b. A cubic function that models the data is with x = 0 representing 1900. The figure shows the graph of the unrounded model on the same axes with the data points. Copyright © 2017, 2013, 2010 Pearson Education, Inc. 16

Example: (cont) c. A quartic function that models the data is with x = 0 representing 1900. The figure shows the graph of the unrounded model on the same axes with the data points. Copyright © 2017, 2013, 2010 Pearson Education, Inc. 17

Example: (cont) d. Cubic: SSE 34. 465 Quartic: 1. 873 average error f(160) 1. 347 28. 76 0. 314 -40. 23 To predict the U. S. population that were foreign born in year 2060, the better model is cubic model because the prediction by the quartic model is negative which does not make common sense. Copyright © 2017, 2013, 2010 Pearson Education, Inc. 18