Section 6 1 Section Check Section 6 2

Section 6. 1 Section Check

Section 6. 2 Circular Motion Uniform Circular Motion

Section 6. 2 Circular Motion • Acceleration is the time rate of change in velocity of an object. • Any time an object is changing its velocity, it is accelerating. • Anytime object changing speed experiences acceleration, but is that the only way?

Section 6. 2 Circular Motion Distinct Ways That A Vector Quantity Can Be Changed • Recall that velocity is a vector quantity. A vector can be changed by • (i) Changing the magnitude of the vector • (ii) Changing the direction of the vector • (iii) Changing both the magnitude and direction of the vector

Section 6. 2 Circular Motion Distinct Ways That The Velocity of An Object Can Be Changed An object will therefore experience an acceleration if (i) The speed of the object can change while it travels in a straight line (ii) The direction of travel of the object can change while it travels at constant speed (iii) The object can change speed and change direction at the same time

Section 6. 2 Circular Motion • An object moving a constant speed but moving in a circular path is called: • Circular Motion – speed stays the same but direction changes→acceleration is occuring)

Section 6. 2 Circular Motion • An object moving along a circular path is not traveling in a straight line. This means that you cannot use the straight-line kinematics formulas developed in previous lessons to describe the motion of such an object.

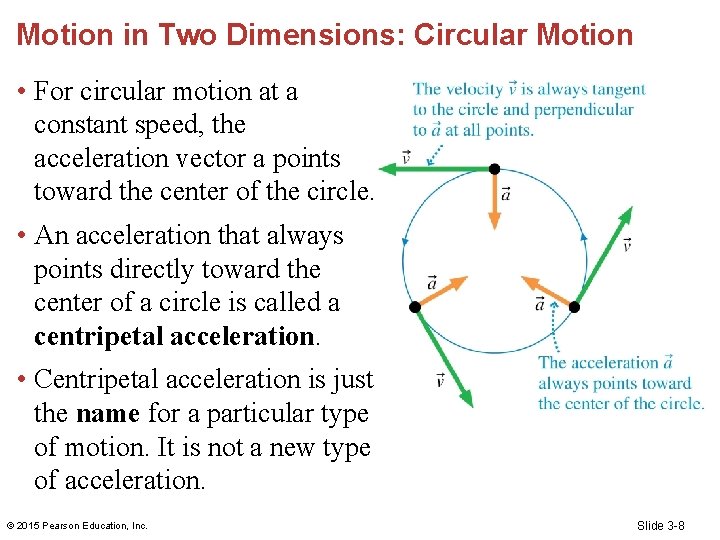
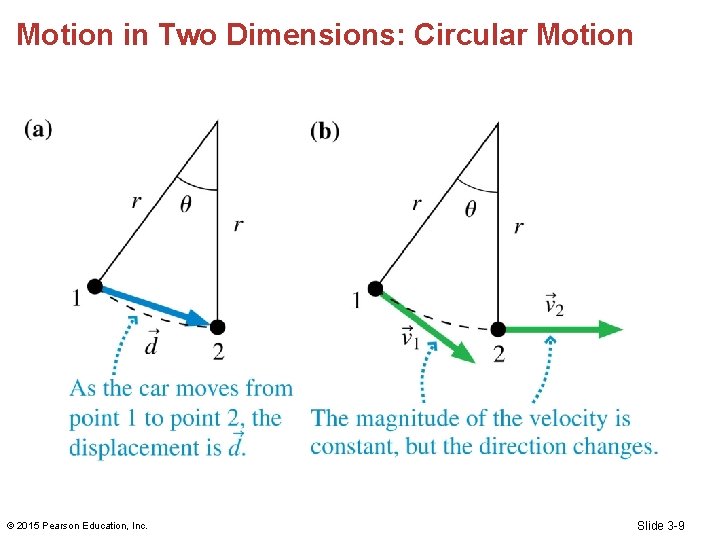
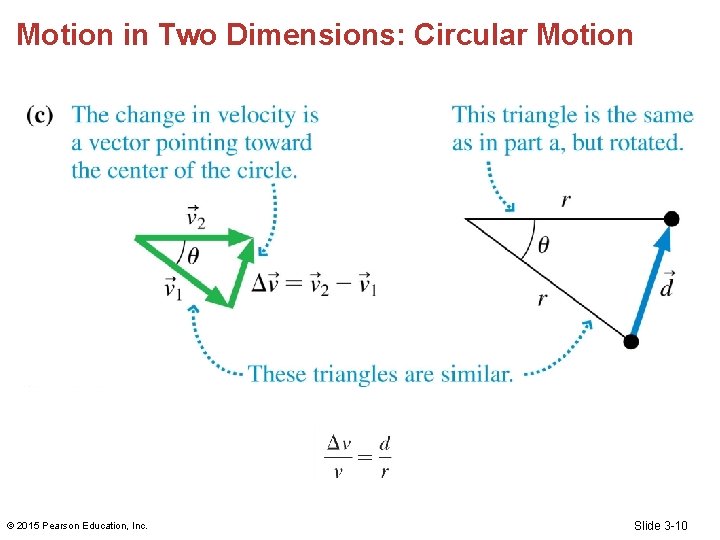
Motion in Two Dimensions: Circular Motion • For circular motion at a constant speed, the acceleration vector a points toward the center of the circle. • An acceleration that always points directly toward the center of a circle is called a centripetal acceleration. • Centripetal acceleration is just the name for a particular type of motion. It is not a new type of acceleration. © 2015 Pearson Education, Inc. Slide 3 -8

Motion in Two Dimensions: Circular Motion © 2015 Pearson Education, Inc. Slide 3 -9

Motion in Two Dimensions: Circular Motion © 2015 Pearson Education, Inc. Slide 3 -10

Motion in Two Dimensions: Circular Motion © 2015 Pearson Education, Inc. Slide 3 -11

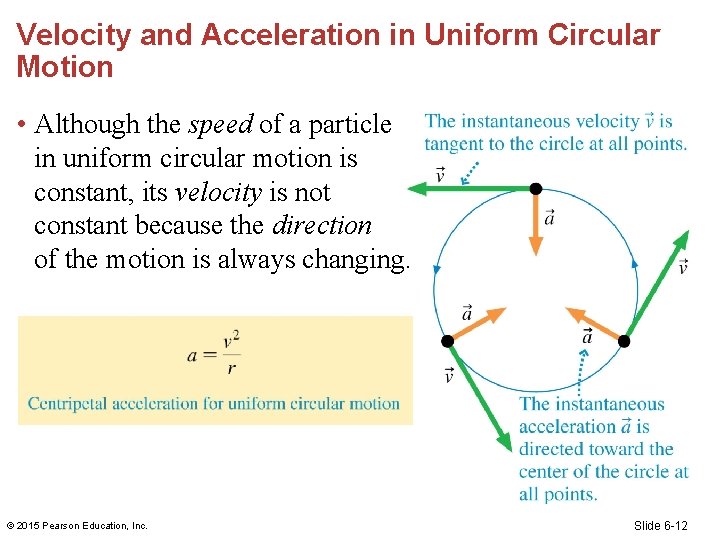
Velocity and Acceleration in Uniform Circular Motion • Although the speed of a particle in uniform circular motion is constant, its velocity is not constant because the direction of the motion is always changing. © 2015 Pearson Education, Inc. Slide 6 -12

Section 6. 2 Circular Motion The time it takes to go around a circle once is called: Period (T) The distance around a circle is called circumference (c) c=πd or 2πr r v

Section 6. 2 Circular Motion Centripetal Acceleration One way of measuring the speed of an object moving in a circle is to measure its period, T, the time needed for the object to make one complete revolution. During this time, the object travels a distance equal to the circumference of the circle, 2πr. The object’s speed, then, is represented by v = 2πr/T.

Section 6. 2 Circular Motion A Quick Summary An object traveling in a circular path at constant velocity does indeed experience an acceleration. This acceleration is toward the center of the circular path at all times. The velocity vector for the object is always tangent to the circle. NOTE: The expressions from straight line kinematics cannot be applied to the motion of such an object.

Section 6. 2 Circular Motion Centripetal Acceleration The acceleration of an object moving in a circle is always in the direction of the net force acting on it, there must be a net force toward the center of the circle. This force can be provided by any number of agents. When an Olympic hammer thrower swings the hammer, the force is the tension in the chain attached to the massive ball.

Section 6. 2 Circular Motion Centripetal Acceleration When an object moves in a circle, the net force toward the center of the circle is called the centripetal force. To analyze centripetal acceleration situations accurately, you must identify the agent of the force that causes the acceleration. Then you can apply Newton’s second law for the component in the direction of the acceleration in the following way.

Section © Circular Motion 6. 2 2 0 1 4 P e a r s o n E d u c a t i o n , So for UCM ∑Fnet is now : Circular motion component form of Newton's second law

Section © Circular Motion 6. 2 2 0 1 5 P e a r s o n E d u c a t i o n , is not a new kind of force: The is due to a force such as tension, friction, or the normal force. We call this centripetal force (center seeking)

Section 6. 2 Section Check Question 1 Explain why an object moving in a circle at a constant speed is accelerating.

Section 6. 2 Section Check Answer 1 Acceleration is the rate of change of velocity, the object is accelerating due to its constant change in the direction of its motion.

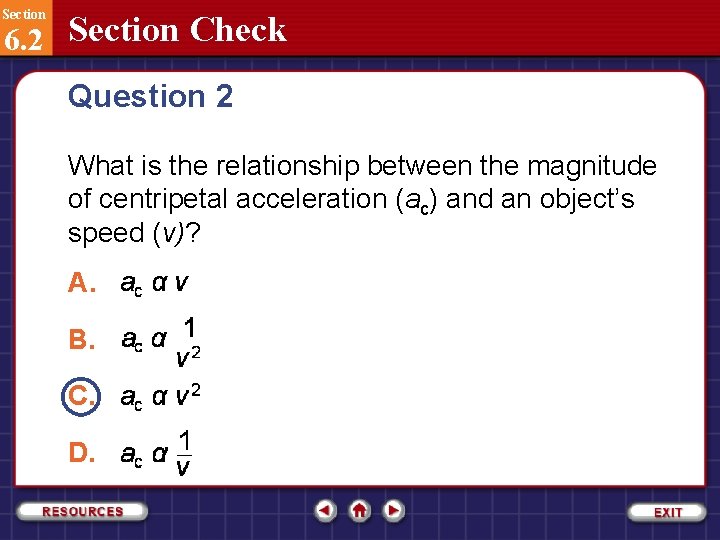
Section 6. 2 Section Check Question 2 What is the relationship between the magnitude of centripetal acceleration (ac) and an object’s speed (v)? A. B. C. D.

Section 6. 2 Section Check Answer 2 Reason: From the equation for centripetal acceleration: Centripetal acceleration always points to the center of the circle. Its magnitude is equal to the square of the speed divided by the radius of the motion.

Section 6. 2 Section Check Question 3 What is the direction of the velocity vector of an accelerating object? A. toward the center of the circle B. away from the center of the circle C. along the circular path D. tangent to the circular path

Section 6. 2 Section Check Answer 3 Reason: While constantly changing, the velocity vector for an object in uniform circular motion is always tangent to the circle. Vectors are never curved and therefore cannot be along a circular path.

Section © Section Check 6. 2 2 0 1 5 P e a r s o n E d u c a t i o n , • A ball at the end of a string is being swung in a horizontal circle. What force is producing the centripetal acceleration of the ball? – Gravity – Air resistance – Normal force – Tension in the string

Section © Section Check 6. 2 2 0 1 5 P e a r s o n E d u c a t i o n , • A ball at the end of a string is being swung in a horizontal circle. What force is producing the centripetal acceleration of the ball? – Gravity – Air resistance – Normal force – Tension in the string

Section © Section Check 6. 2 2 0 1 5 P e a r s o n E d u c a t i o n , • A ball at the end of a string is being swung in a horizontal circle. What is the direction of the net force on the ball? – Tangent to the circle – Toward the center of the circle – There is no net force.

Section © Section Check 6. 2 2 0 1 5 P e a r s o n E d u c a t i o n , • A ball at the end of a string is being swung in a horizontal circle. What is the direction of the net force on the ball? – Tangent to the circle – Toward the center of the circle – There is no net force.

Section © Section Check 6. 2 2 0 1 5 P e a r s o n E d u c a t i o n , • A coin is rotating on a turntable; it moves without sliding. At the instant shown in the figure, which arrow gives the direction of the coin’s velocity?

Section © Section Check 6. 2 2 0 1 5 P e a r s o n E d u c a t i o n , • A coin is rotating on a turntable; it moves without sliding. At the instant shown in the figure, which arrow gives the direction of the coin’s velocity? A

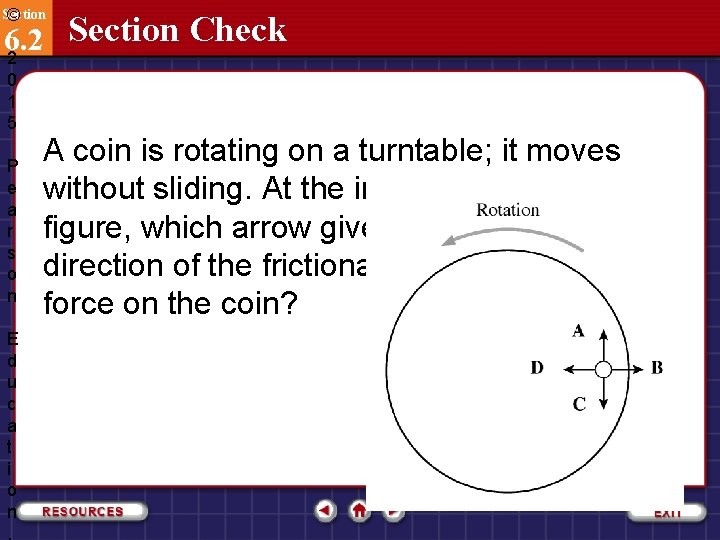
Section © Section Check 6. 2 2 0 1 5 P e a r s o n E d u c a t i o n , A coin is rotating on a turntable; it moves without sliding. At the instant shown in the figure, which arrow gives the direction of the frictional force on the coin?

Section © Section Check 6. 2 2 0 1 5 P e a r s o n E d u c a t i o n , A coin is rotating on a turntable; it moves without sliding. At the instant shown in the figure, which arrow gives the direction of the frictional force on the coin? D

Section © Section Check 6. 2 2 0 1 5 P e a r s o n E d u c a t i o n , A coin is rotating on a turntable; it moves without sliding. At the instant shown, suppose the frictional force disappeared. In what direction would the coin move?

Section © Section Check 6. 2 2 0 1 5 P e a r s o n E d u c a t i o n , A coin is rotating on a turntable; it moves without sliding. At the instant shown, suppose the frictional force disappeared. In what direction would the coin move? A