Section 5 6 Resource Management Examples I see

Section 5. 6 Resource Management Examples

I see how the fish animation is an example of recursion 1. Absolutely 2. Sort of 3. Not a clue 0 of 30 Explain: 2

Fish Population 1500 Fish last year - 40% of fish last year + 700 at end of last year = Fish this year ? 3

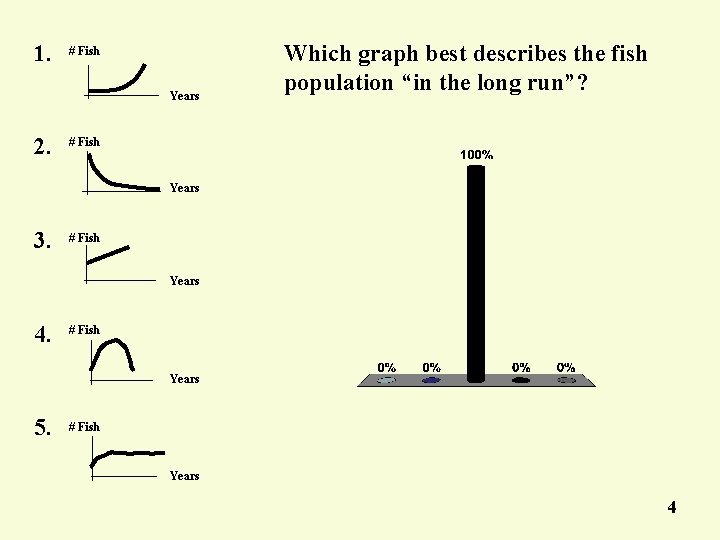
1. # Fish Years 2. Which graph best describes the fish population “in the long run”? # Fish Years 3. # Fish Years 4. # Fish Years 5. # Fish Years 4

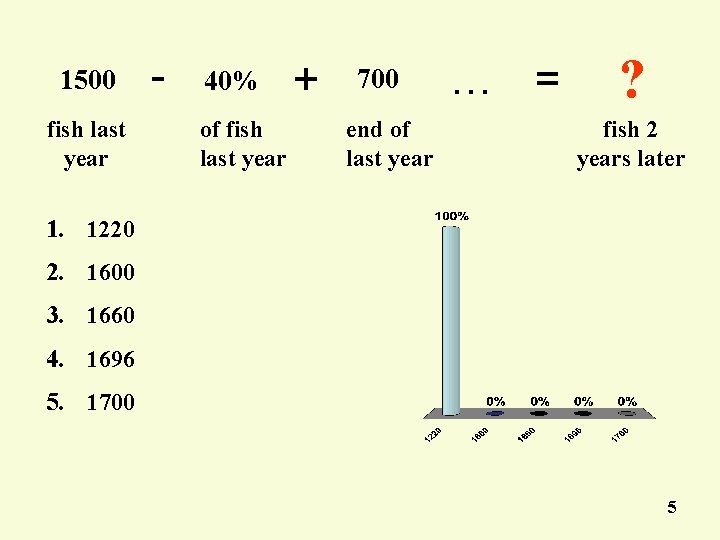
1500 fish last year - 40% of fish last year + 700 end of last year … = ? fish 2 years later 1. 1220 2. 1600 3. 1660 4. 1696 5. 1700 5

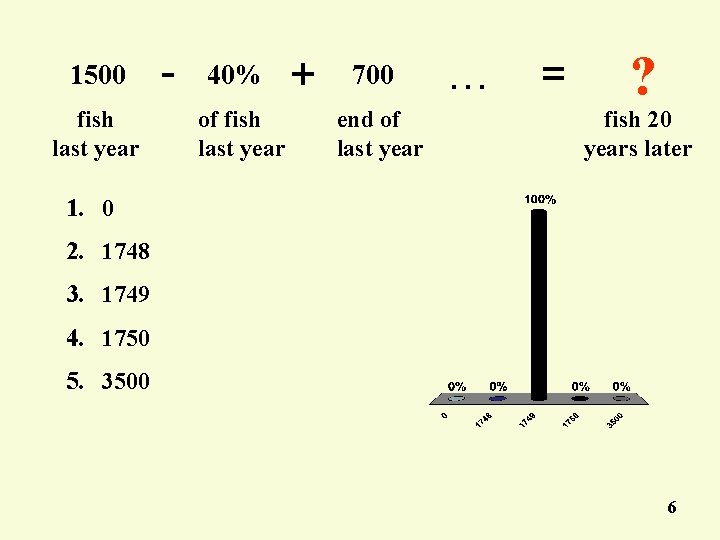
1500 fish last year - 40% of fish last year + 700 end of last year … = ? fish 20 years later 1. 0 2. 1748 3. 1749 4. 1750 5. 3500 6

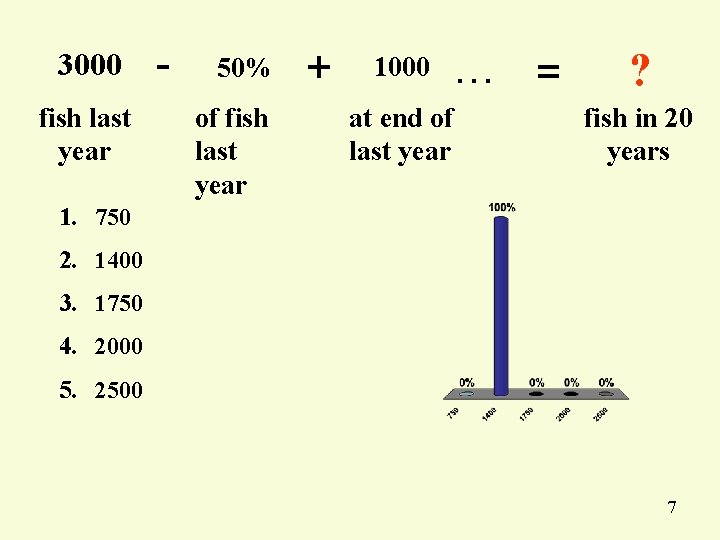
3000 fish last year - 50% of fish last year + 1000 at end of last year … = ? fish in 20 years 1. 750 2. 1400 3. 1750 4. 2000 5. 2500 7

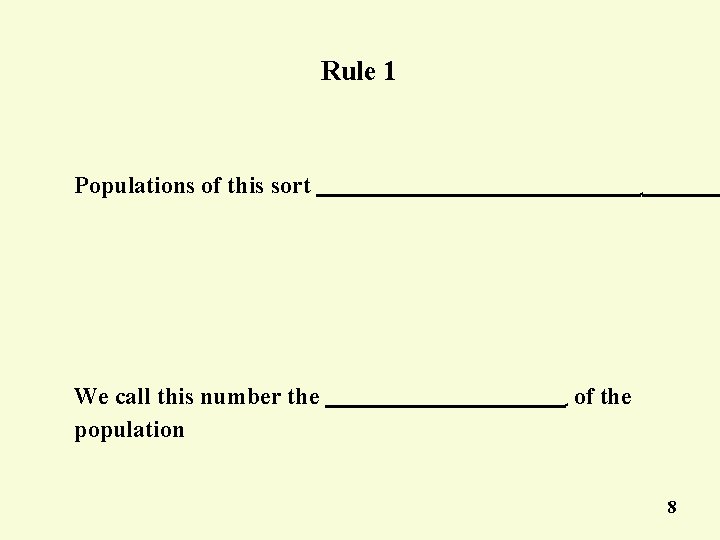
Rule 1 Populations of this sort We call this number the population . . of the 8

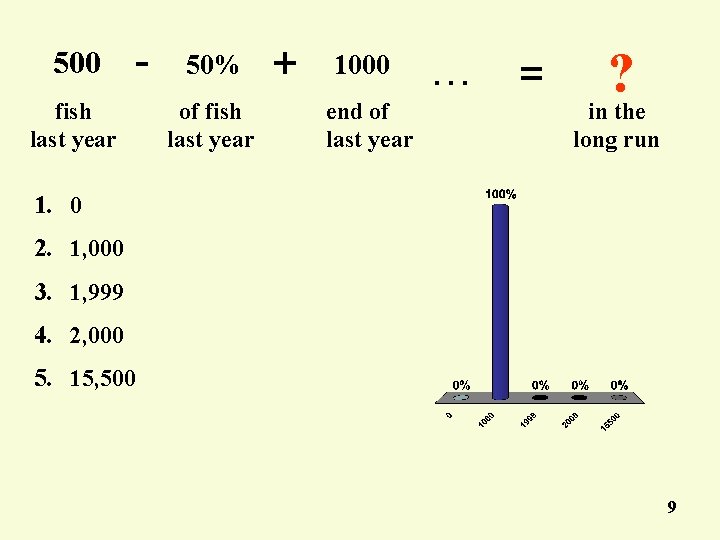
500 - fish last year 50% of fish last year + 1000 end of last year … = ? in the long run 1. 0 2. 1, 000 3. 1, 999 4. 2, 000 5. 15, 500 9

Graphs Rule 2 If you change only the population always , . . 10

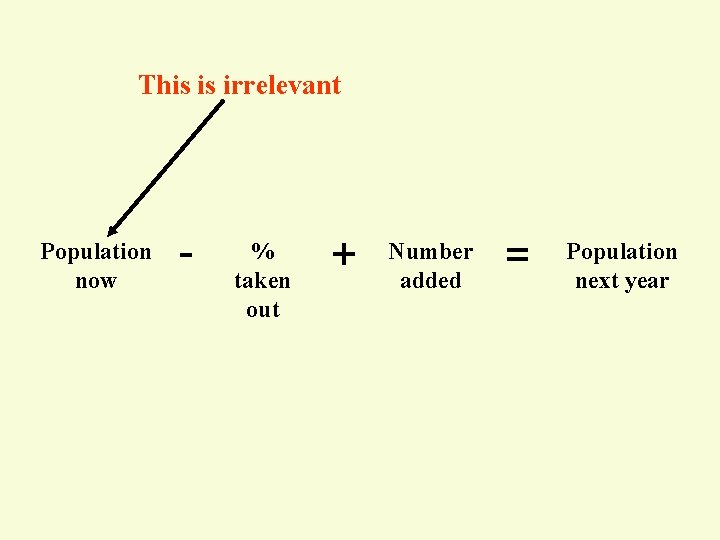
This is irrelevant Population now - % taken out + Number added = Population next year

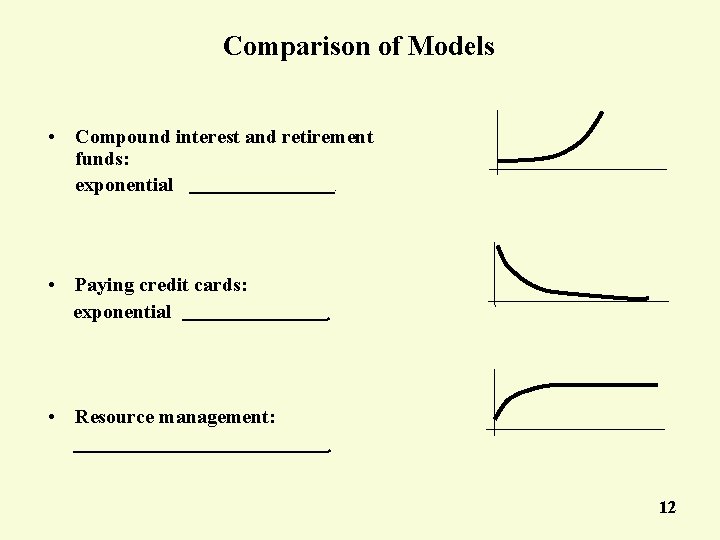
Comparison of Models • Compound interest and retirement funds: exponential. • Paying credit cards: exponential . • Resource management: . 12

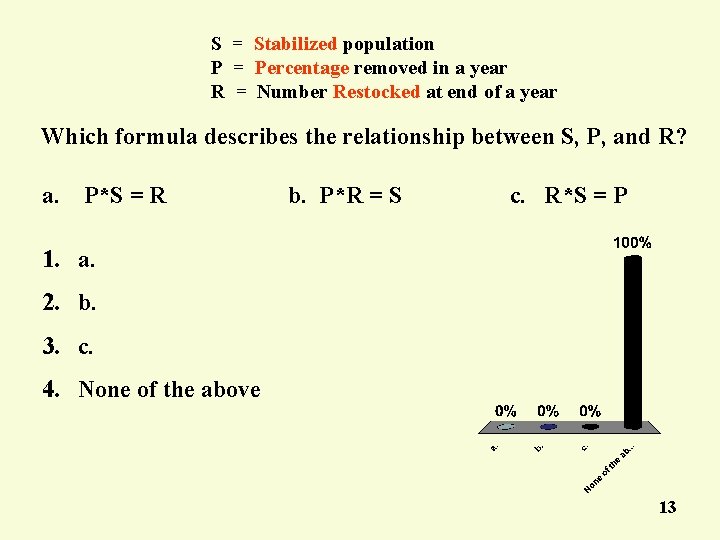
S = Stabilized population P = Percentage removed in a year R = Number Restocked at end of a year Which formula describes the relationship between S, P, and R? a. P*S = R b. P*R = S c. R*S = P 1. a. 2. b. 3. c. 4. None of the above 13

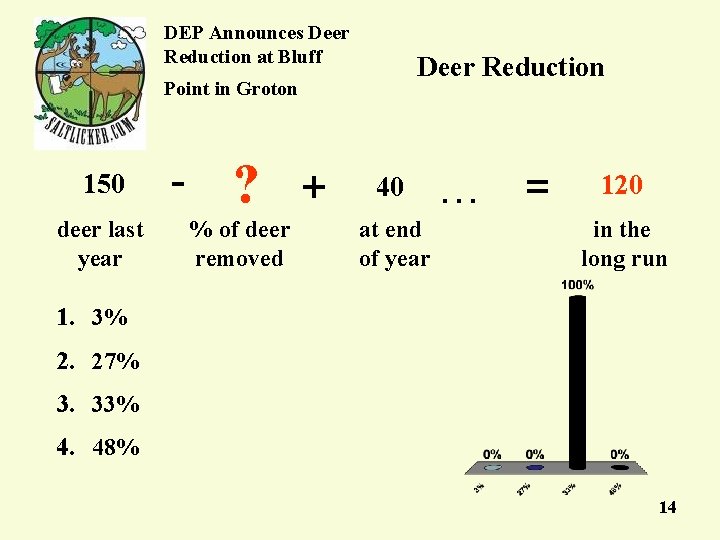
DEP Announces Deer Reduction at Bluff Deer Reduction Point in Groton 150 deer last year - ? + % of deer removed 40 at end of year … = 120 in the long run 1. 3% 2. 27% 3. 33% 4. 48% 14

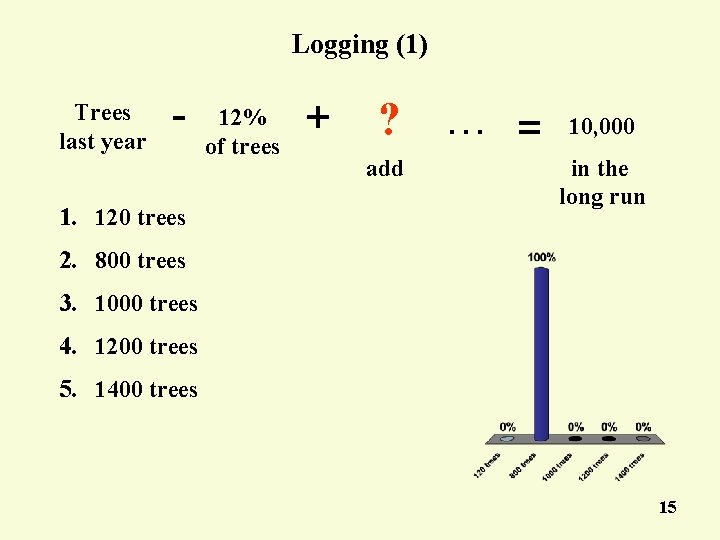
Logging (1) Trees last year - 1. 120 trees 12% of trees + ? add … = 10, 000 in the long run 2. 800 trees 3. 1000 trees 4. 1200 trees 5. 1400 trees 15

Logging (2) After 3 years a fire destroys half the forest. You continue to cut 12% of the trees annually. You add trees each year What will be the stabilizing value of the forest? 1. 500 2. 750 3. 1, 000 4. 1, 250 5. 10, 000 16

Henry is the sole inheritor of his father’s estate. He doesn’t know its current value, but he does know that his father withdraws 20% of it annually. Then at the end of the year he adds $300, 000 to the estate. How much can Henry expect to receive “in the long run”? 1. $60, 000 2. $150, 000 3. $240, 000 4. $1, 500, 000 5. $3, 000 17

End of 5. 6 18

Resource Management

“Fish Population” Fish now = Fish at start of last year - 40% of fish during last year + 700 at end of last year Game Warde n 20

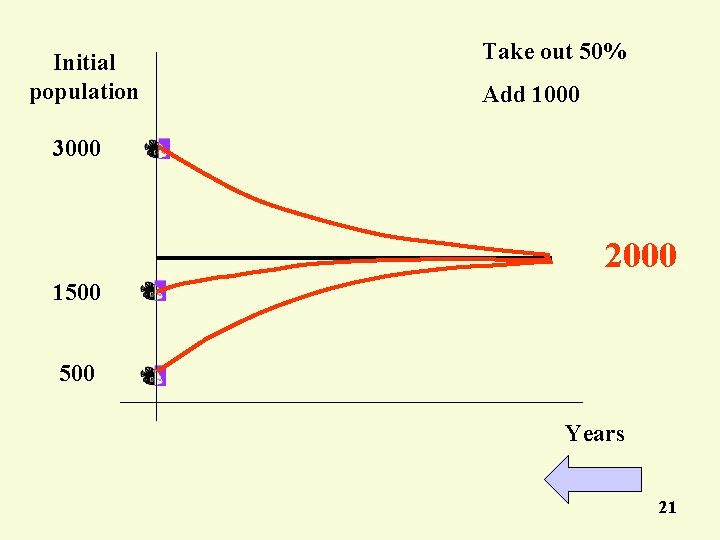
Initial population Take out 50% Add 1000 3000 2000 1500 Years 21

Meta - Material 22