Section 5 5 Solving Trigonometric Equations 1 Solving

Section 5. 5 Solving Trigonometric Equations 1

Solving Trigonometric Equations To solve trigonometric equations: Use standard algebraic techniques learned in Algebra II. Look for factoring and collecting like terms. Isolate the trig function in the equation. Use the inverse trig functions to assist in determining solutions. Solutions: on the interval [0, 2 ) or all solutions (using periodic properties) You are responsible for checking your solutions back into the original problem! 2

Solving Trigonometric Equations 1. Solve: Step 1: Isolate sin x using algebraic skills. Step 2: Solve using the correct quadrants on the unit circle. 3

Solving Trigonometric Equations # 22 Solution: 4

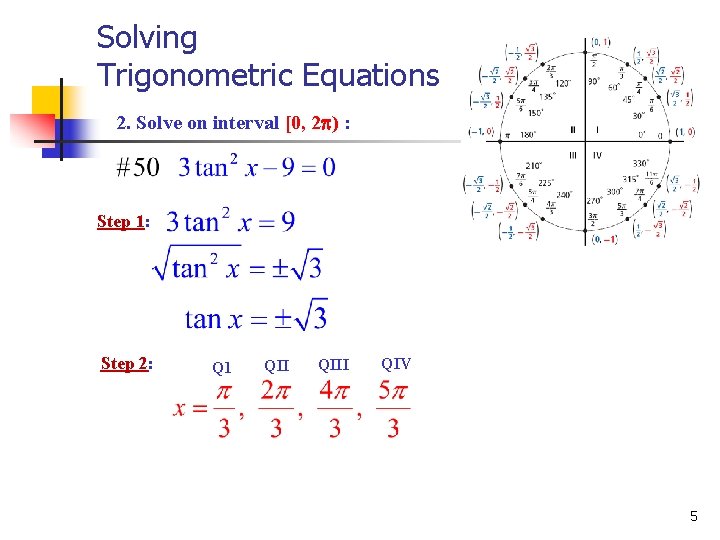
Solving Trigonometric Equations 2. Solve on interval [0, 2 ) : Step 1: Step 2: Q 1 QIII QIV 5

Solving Trigonometric Equations # 48 Solve on interval [0, 2 ): Solution: 6

Solving Trigonometric Equations 3. Solve on interval [0, 2 ): Step 1: Step 2: Note: There is no solution here because 2 lies outside the range for cosine. 7

Solving Trigonometric Equations Solve on interval [0, 2 ): #56 8

Solving Trigonometric Equations 4. Solve on interval [0, 2 ): Factor the quadratic equation. Set each factor equal to zero. Solve for sin x Determine the correct quadrants for the solution(s). 9

Solving Trigonometric Equations 5. Solve on interval [0, 2 ): Replace sin 2 x with 1 -cos 2 x Distribute Combine like terms. Multiply through by – 1. Factor. Set factor equal to zero. Solve for cos x. Determine the solution(s). 10

Solving Trigonometric Equations 6. Solve on interval [0, 2 ): Square both sides of the equation FOIL or Double Distribute Replace (sin 2 x + cos 2 x) with 1 Subtract 1 from both sides. Why are 0 and /2 removed from solutions? Divide both sides by 2 Set each factor equal to zero. X X Determine the solution(s). 11

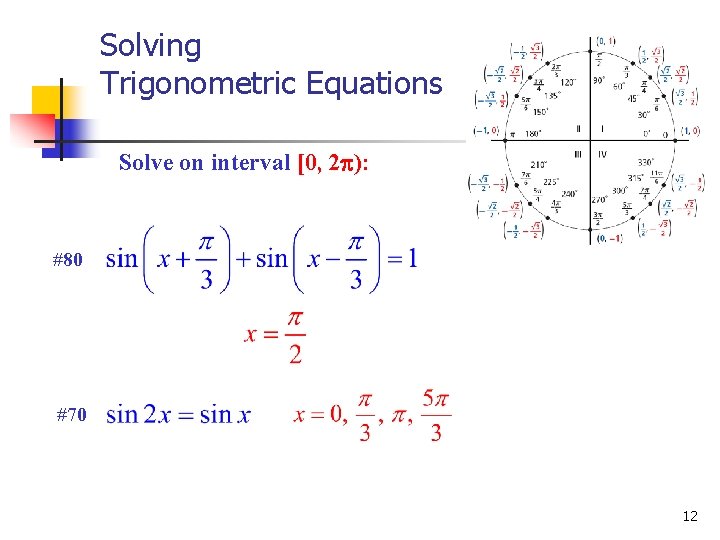
Solving Trigonometric Equations Solve on interval [0, 2 ): #80 #70 12

Solving Trigonometric Equations 7. Solve on interval [0, 2 ): Solution: No algebraic work needs to be done because cosine is already isolated. Here, 3 x refers to an angle, and the equation cannot be divided by 3 because it is cos(3 x) which equals ½. Since 3 x refers to an angle, find the angles whose cosine value is ½. Now divide by 3 to solve for x. Obtained solutions do not exceed 2. Therefore, more solutions may exist. 13

Solving Trigonometric Equations 7. Solve on interval [0, 2 ): Solution continues: We could use periodic property of cosine, and write the general form of the solution of this equation using a period for the function : The general solution for this equation will be: We need to solve this equation on interval [0, 2 ): 14

Solving Trigonometric Equations 7. Solve on interval [0, 2 ): Solution continues: We will be assigning and calculating x–values making sure not to exceed Think about it as a repeated addition of period to initially obtained solutions and 15

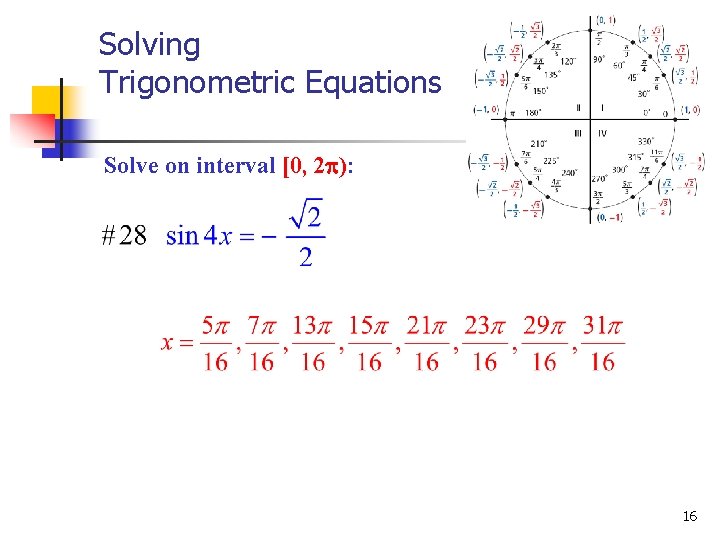
Solving Trigonometric Equations Solve on interval [0, 2 ): 16

Solving Trigonometric Equations Solve on interval [0, 2 ): 17

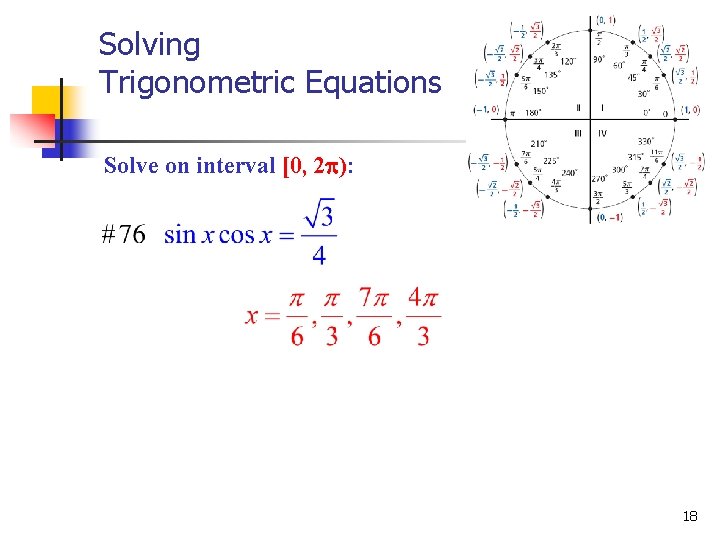
Solving Trigonometric Equations Solve on interval [0, 2 ): 18

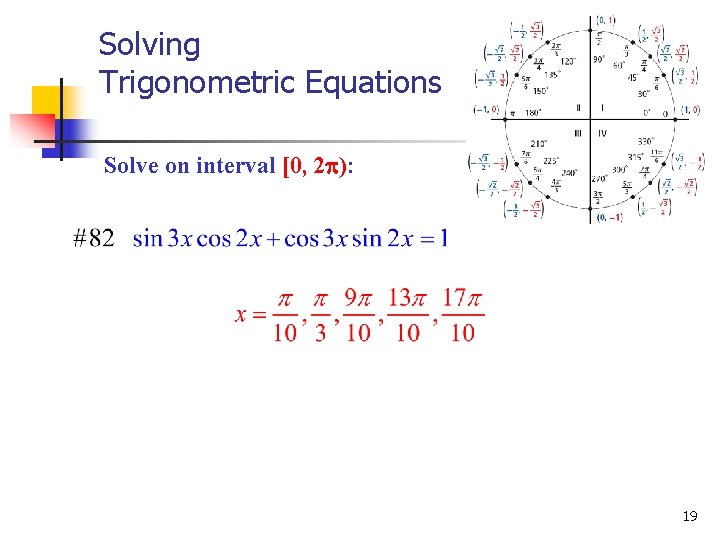
Solving Trigonometric Equations Solve on interval [0, 2 ): 19

Solving Trigonometric Equations What you should know: 1. How to use algebraic techniques to solve trigonometric equations. 2. How to solve quadratic trigonometric equations by factoring or the quadratic formula. 3. How to solve trigonometric equations involving multiple angles. 20