Section 5 5 Fibonaccis Problem 5 5 Fibonaccis

Section 5. 5 Fibonacci’s Problem 5. 5 Fibonacci's Rabbits 1

“Fibonacci” (Leonardo de Pisa) 1170 -1240 And this man’s claim to fame is …? 5. 5 Fibonacci's Rabbits 2

5. 5 Fibonacci's Rabbits 3

Rabbit Rules 1. All pairs of rabbits consist of a male and female 2. One pair of newborn rabbits is placed in hutch on January 1 3. When this pair is 2 months old they produce a pair of baby rabbits 4. Every month afterwards they produce another pair 5. All rabbits produce pairs in the same manner 6. Rabbits don’t die 5. 5 Fibonacci's Rabbits 4

The Fibonacci Rabbit Problem How many pairs of rabbits will there be 12 months later? 5. 5 Fibonacci's Rabbits 5

How many pairs of rabbits will there be on June 1? 1. 5 2. 7 3. 8 4. 11 5. 13 5. 5 Fibonacci's Rabbits 6

0 Jan 1 1 Feb 1 2 Mar 1 0 5. 5 Fibonacci's Rabbits 7

2 Mar 1 0 Apr 1 3 1 0 4 May 1 2 1 0 0 5. 5 Fibonacci's Rabbits 8

Apr 1 May 1 June 1 3 1 0 4 2 1 0 0 5 3 2 1 1 5. 5 Fibonacci's Rabbits 9

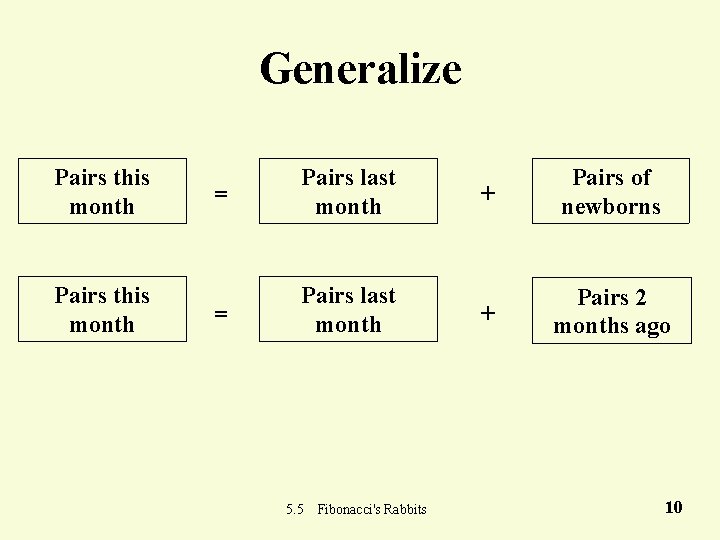
Generalize Pairs this month = Pairs last month 5. 5 Fibonacci's Rabbits + Pairs of newborns + Pairs 2 months ago 10

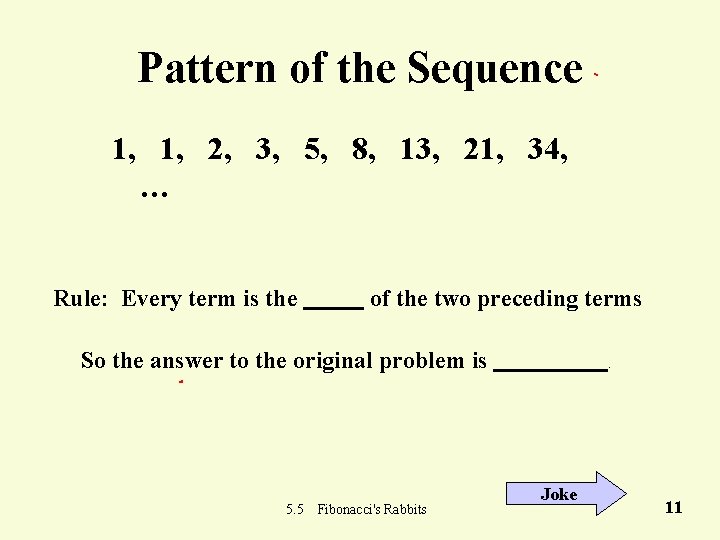
Pattern of the Sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, … Rule: Every term is the of the two preceding terms So the answer to the original problem is 5. 5 Fibonacci's Rabbits . Joke 11

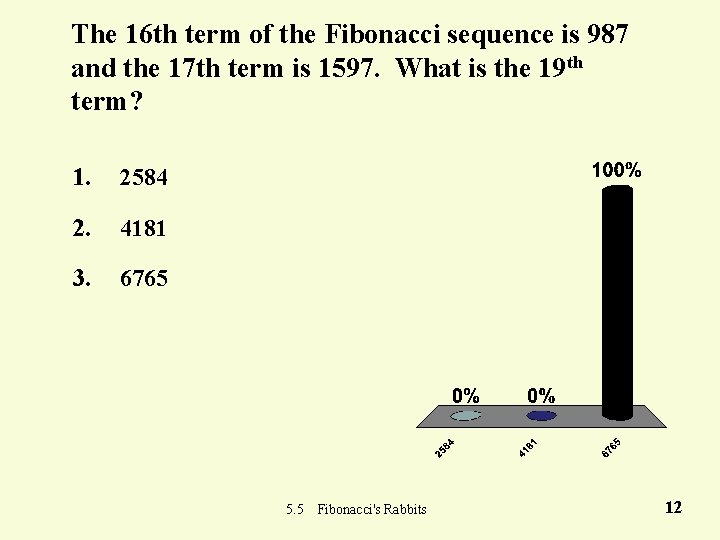
The 16 th term of the Fibonacci sequence is 987 and the 17 th term is 1597. What is the 19 th term? 1. 2584 2. 4181 3. 6765 5. 5 Fibonacci's Rabbits 12

Change Fibonacci’s problem slightly so that each pair of adult rabbits produces 2 pairs per litter. Which recursion formula best describes the rabbit population? 1. This month = Last month + (Two months ago) 2. This month = Last month + 2*(Two months ago) 3. This month = 2*Last month + (Two months ago) 5. 5 Fibonacci's Rabbits 13

As in the last problem assume that each pair produces 2 pairs per litter from the second month on. How many pairs will there be in 5 months? 1. 8 2. 10 3. 11 5. 5 Fibonacci's Rabbits 14

New Problem: Assume each pair of adult rabbits produces one pair monthly from the 4 th month on. Which recursive formula best describes the rabbit population? 1. This month = Last month + (Four months ago) 2. This month = Last month + 3*(Four months ago) 3. This month = Last month + 4*(Four months ago) 5. 5 Fibonacci's Rabbits 15

As in last problem, assume each pair of adult rabbits produces one pair monthly from the 4 th month on. How many pairs of rabbits will there be in 7 months? 1. 5 2. 8 3. 13 4. 21 5. 5 Fibonacci's Rabbits 16

Exponential Growth 1 1 2 3 5 8 13 21 34 55 89 144 46, 368 2 years 14, 930, 352 3 years 4, 807, 526, 976 4 years 1 year Examples 5. 5 Fibonacci's Rabbits 17

End of 5. 5 Fibonacci's Rabbits 18

Music Fibonacci Suite for retuned piano, seven hands 5. 5 Fibonacci's Rabbits 19

Chromatic Scale Fibonacci numbers? 5. 5 Fibonacci's Rabbits 20

Botany 5 Spirals 5. 5 Fibonacci's Rabbits 21

One-petaled. . . white calla lily 5. 5 Fibonacci's Rabbits 22

Two-petaled flowers… euphorbia 5. 5 Fibonacci's Rabbits 23

Three petals… trillium 5. 5 Fibonacci's Rabbits 24

Five petals morning glory 5. 5 Fibonacci's Rabbits 25

Eight-petaled… bloodroot 5. 5 Fibonacci's Rabbits 26

Thirteen. . . black-eyed susan 5. 5 Fibonacci's Rabbits 27

Twenty-one… shasta daisy with 21 petals 5. 5 Fibonacci's Rabbits 28

Poetry I am sitting quietly, listening for the quiet noises in the darkness, ghostly images flying between the tall pine trees, illusion created by the mind, made by shadows, the brain playing tricks on itself. It sits there, the raven, black as night, looking at me with its dark eyes in the dark night. Inspiration comes. Words form in my head. Evermore. Jim T. Henriksen 5. 5 Fibonacci's Rabbits 29

“Fibs” Six line, 20 syllable poem One Small, Precise, Poetic, Spiraling mixture: Math plus poetry yields the Fib 5. 5 Fibonacci's Rabbits 30

Investments Robert Fischer, leader of the Fibonacci approach to trading 5. 5 Fibonacci's Rabbits 31

Education 5. 5 Fibonacci's Rabbits 32

Algebra 1 1 2 3 5 8 13 21 34 55 … * 21 = 441 5. 5 * Fibonacci's Rabbits = 442 33

Fibonacci and the Greeks 1, 1, 2, 3, 5, 8, 13, 21, 34, … 1/1 = 1 2/1 3/2 5/3 8/5 13/8 21/13 34/21 55/34 89/55 144/89 233/144 = = = 2 1. 5 1. 666666… 1. 625 1. 6153846… 1. 6190476… 1. 6176470… 1. 6181818… 1. 6179775… 1. 6180555… 5. 5 Fibonacci's Rabbits 34

Golden Number 1. 61808… 5. 5 Fibonacci's Rabbits 35

Golden Rectangle 1. 618 1 5. 5 Fibonacci's Rabbits 36

Classical Art Mona Lisa 5. 5 Fibonacci's Rabbits 37

Parthenon - Athens 5. 5 Fibonacci's Rabbits 38

The Vitruvian Man 5. 5 Fibonacci's Rabbits 39

Spiral Generated by Golden Ratio 5. 5 Fibonacci's Rabbits 40

The Nautilus Shell 5. 5 Fibonacci's Rabbits 41

Modern Art Piet Mondrian 5. 5 Fibonacci's Rabbits 42

Diets and Fitness 5. 5 Fibonacci's Rabbits 43

Mo and the Boys There are 100 measures in the first movement. The first section, with theme, has 32 measures, and the last section, with theme variations, has 68 measures. This is a perfect division, using natural numbers, with the golden section. Although there is no physical evidence that Mozart used the Fibonacci sequence in his music, it is still very easy to see the use of perfect divisions. 5. 5 Fibonacci's Rabbits 44

Fibonacci Rap 5. 5 Fibonacci's Rabbits 45

Fibonacci Waltz 5. 5 Fibonacci's Rabbits 46

Lateralus By Tool 5. 5 Fibonacci's Rabbits 47

“Lateralus” (1)Black, (1) then, (2) white are, (3) all I see, (5) in my infancy, (8) red and yellow then came to be, (5) reaching out to me, (3) lets me see. (2) There is, (1) so, 5. 5 (1) much, (2) more that (3) beckons me, (5) to look through to these, (8) infinite possibilities. (13) As below so above and beyond I imagine, (8) drawn outside the lines of reason. (5) Push the envelope. (3) Watch it bend. Fibonacci's Rabbits 48

More lyrics Spiral out Keep going Spiral out! Keep going 5. 5 Fibonacci's Rabbits 49

Facts • Keenan begins singing at 1: 37 into the song. 1 minute 37 seconds, or 97 seconds, is approximately 1. 618 of a full minute. • The time signatures of the chorus change from 9/8 to 8/8 to 7/8; as drummer Danny Carey says, "It was originally titled 9 -8 -7. For the time signatures. Then it turned out that 987 was the 17 th number of the Fibonacci sequence. So that was cool. ” 5. 5 Fibonacci's Rabbits 50

Fibonacci Joke How much does a large order of Fibonaccos cost? . The price of a medium + The price of a small 5. 5 Fibonacci's Rabbits 51

Meta-Material 5. 5 Fibonacci's Rabbits 52