Section 5 4 Using Calculus to Solve Optimization

Section 5. 4 Using Calculus to Solve Optimization Problems 5. 3 Pick up packet out of folder

1. The sum of two nonnegative numbers is 20. Find the numbers (a) if the sum of their squares is to be as large as possible. Let the two numbers be represented by x and 20 – x. makes x = 10 a minimum. Maximum must occur at an endpoint. 0 and 20

1. The sum of two nonnegative numbers is 20. Find the numbers (b) If the product of the square of one number and the cube of the other is to be as large as possible Let the two numbers be represented by x and 20 – x. _ + 12 + 20 Max at 12, y’ changes from pos to neg 12 and 8 Min at 20, y’ changes from neg to pos

1. The sum of two nonnegative numbers is 20. Find the numbers (c) if one number plus the square root of the other is as large as possible. Let the two numbers be represented by x and 20 – x. therefore a max

2. A rectangular pen is to be fenced in using two types of fencing. Two opposite sides will use heavy duty fencing at $3/ft while the remaining two sides will use standard fencing at $1/ft. What are the dimensions of the rectangular plot of greatest area that can be fenced in at a total cost of $3600? 1 y 3 x Therefore max The dimensions of a rectangular plot of greatest area are 300 x 900

3. A rectangular plot is to be bounded on one side by a straight river and enclosed on the other three sides by a fence. With 800 m of fence at your disposal, what is the largest area you can enclose? x x y Therefore a max The largest area you can enclose is 80000

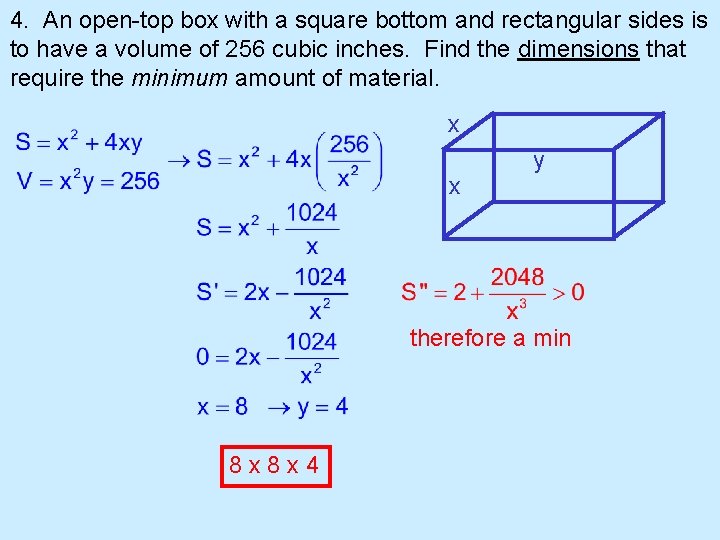
4. An open-top box with a square bottom and rectangular sides is to have a volume of 256 cubic inches. Find the dimensions that require the minimum amount of material. x x y therefore a min 8 x 8 x 4

5. Find the largest possible value of 2 x + y if x and y are the lengths of the sides of a right triangle whose hypotenuse is units long. y x + _ 2 Therefore x = 2 is a max since B’ changes from pos to neg.

6. A right triangle of hypotenuse 5 is rotated about one of its legs to generate a right circular cone. Find the cone of greatest volume. 5 y x Therefore max

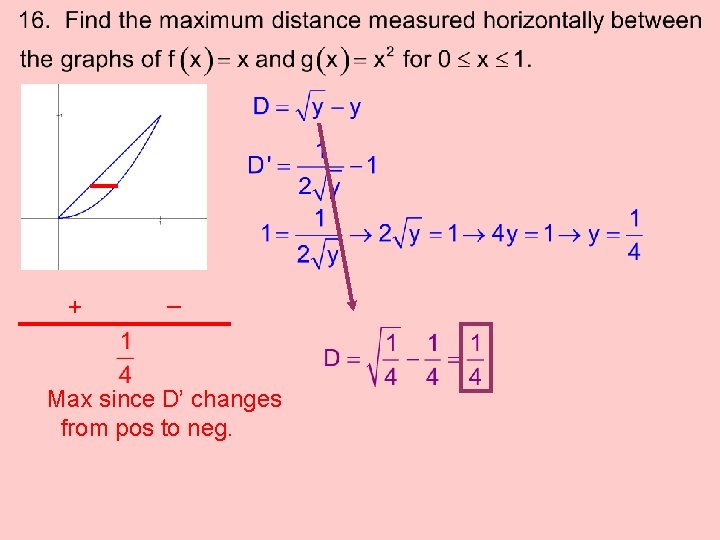
7. Determine the area of the largest rectangle that may be Inscribed under the curve _ + 1 Max since A’ changes from pos to neg

8. (calculator required) A poster is to contain 100 square inches of picture surrounded by a 4 inch margin at the top and bottom and a 2 inch margin on each side. Find the overall dimensions that will minimize the total area of the poster. 2 4 y 4 Since f’ changes from neg to pos, we have a minimum x 2

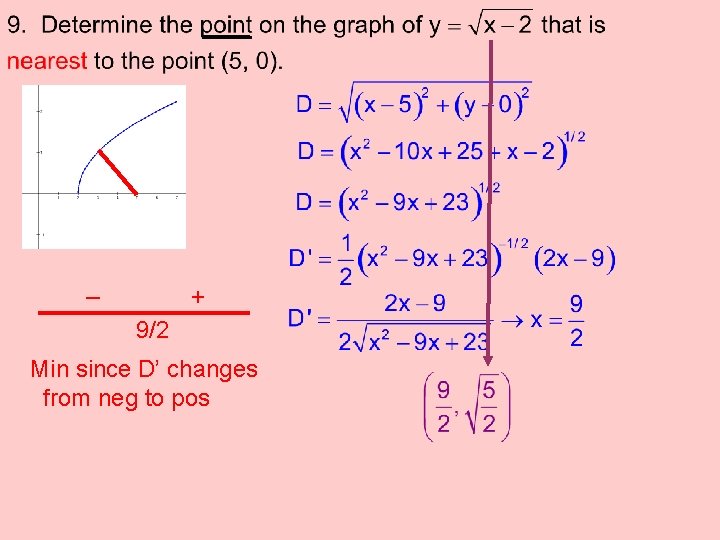
_ + 9/2 Min since D’ changes from neg to pos

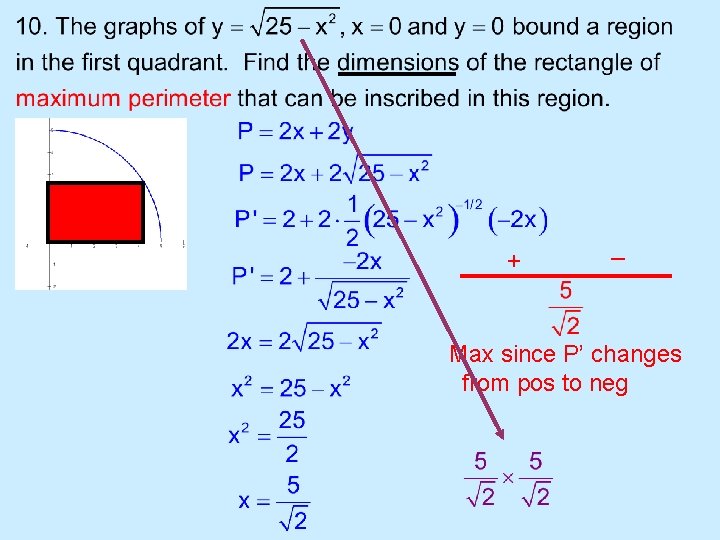
+ _ Max since P’ changes from pos to neg

11. (calculator required) Find the dimensions of the rectangle with maximum area that can be inscribed in a circle of radius 10. Since A’ changes from pos to neg, we have a maximum

Max at x = 7. 46 since f ‘ changes from pos to neg At 7. 46, r = 358. 08, c = 194. 34, or P = 163. 14 Max profit is $163, 000 which occurs when 7460 units are made

13. A tank with a rectangular sides is to be open at the top. It is to be constructed so that its width is 4 m and its volume is 36 cubic meters. If building the tank costs $10 per square meter for the base and $5 per square meter for the sides, what is the cost of the least expensive tank? 4 x y

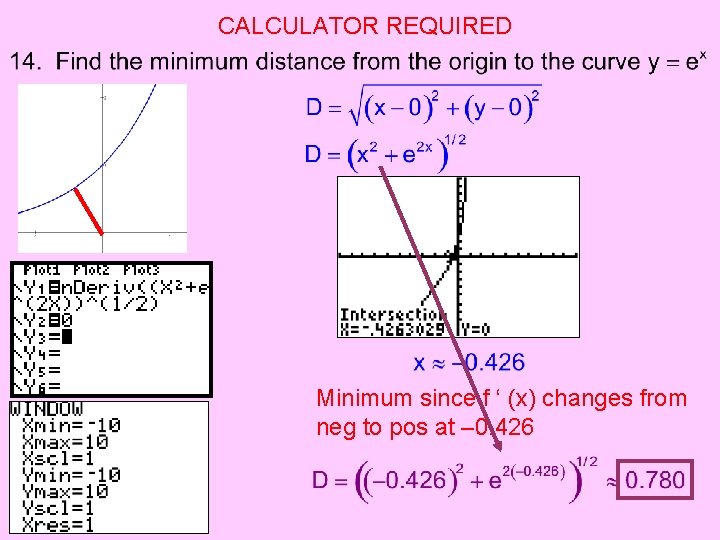
CALCULATOR REQUIRED Minimum since f ‘ (x) changes from neg to pos at – 0. 426

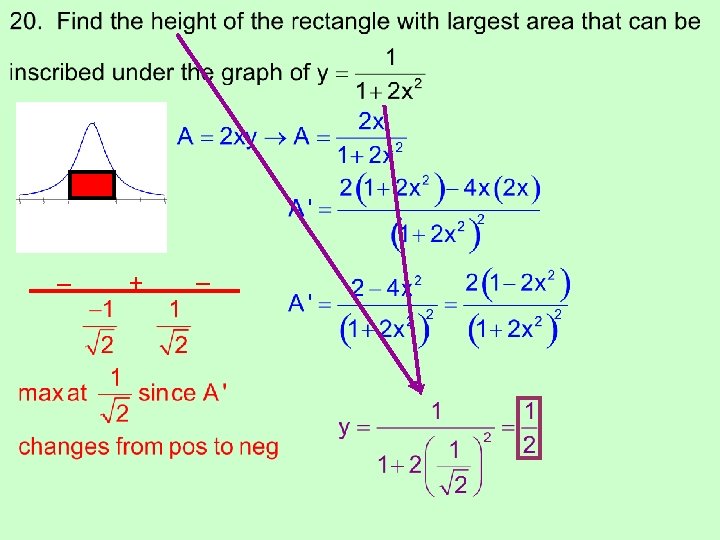
Since A ‘ changes from neg to pos, min area at t = 2

+ _ Max since D’ changes from pos to neg.

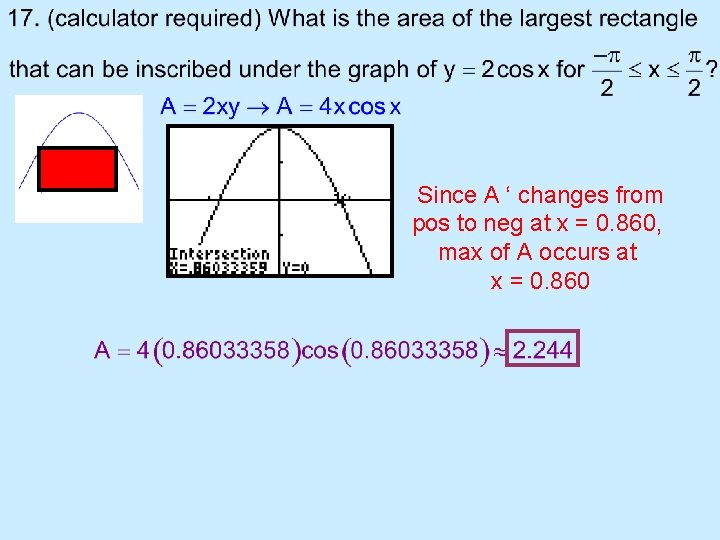
Since A ‘ changes from pos to neg at x = 0. 860, max of A occurs at x = 0. 860

18. Consider the set of all right circular cylinders for which the sum of the height and diameter is 18 inches. What is the radius of the cylinder with the maximum volume? X

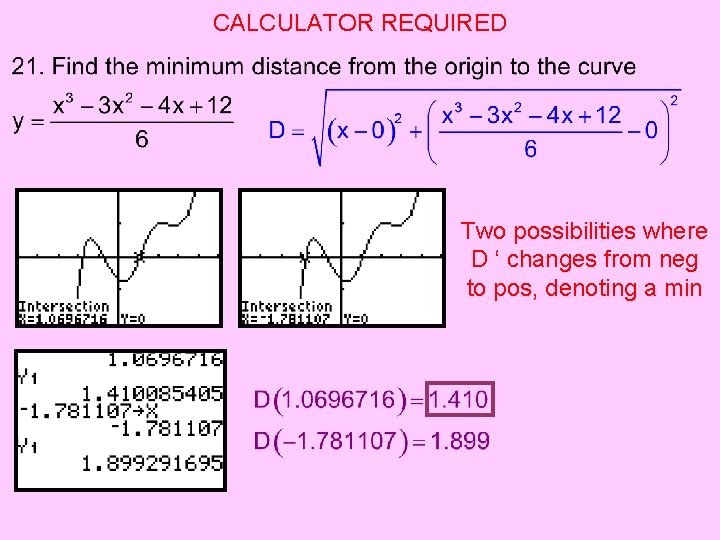
CALCULATOR REQUIRED Two possibilities where D ‘ changes from neg to pos, denoting a min

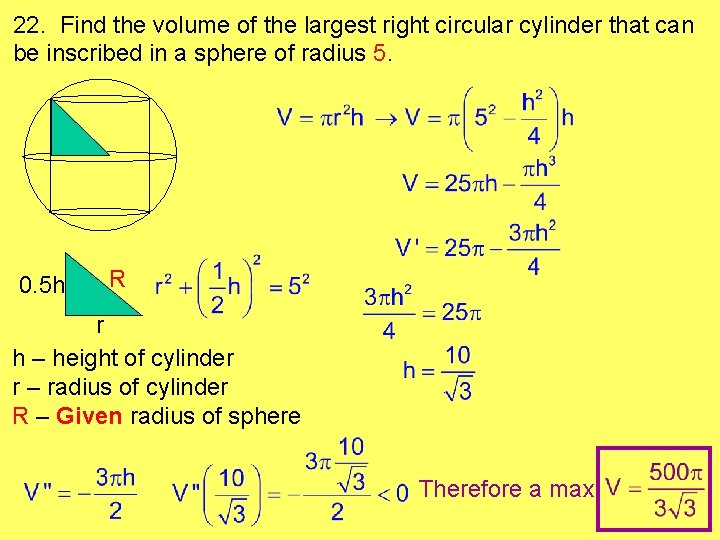
22. Find the volume of the largest right circular cylinder that can be inscribed in a sphere of radius 5. 0. 5 h R r h – height of cylinder r – radius of cylinder R – Given radius of sphere Therefore a max