Section 5 3 Normal Distributions Finding Probabilities Probabilities

Section 5. 3 Normal Distributions Finding Probabilities

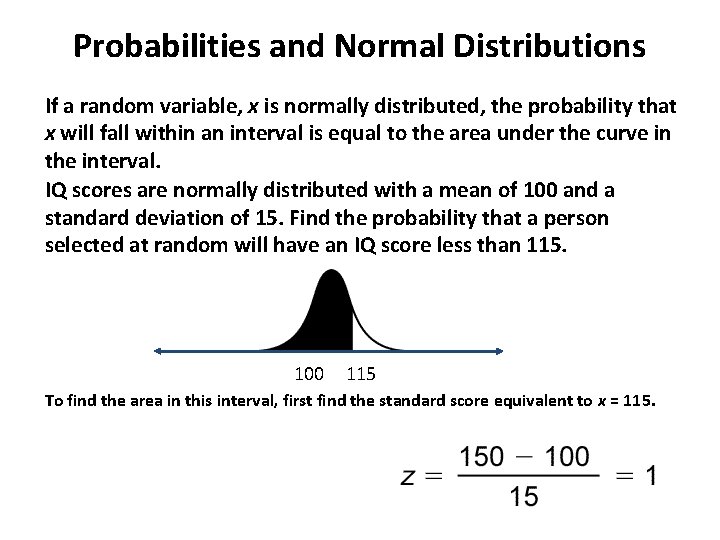
Probabilities and Normal Distributions If a random variable, x is normally distributed, the probability that x will fall within an interval is equal to the area under the curve in the interval. IQ scores are normally distributed with a mean of 100 and a standard deviation of 15. Find the probability that a person selected at random will have an IQ score less than 115. 100 115 To find the area in this interval, first find the standard score equivalent to x = 115.

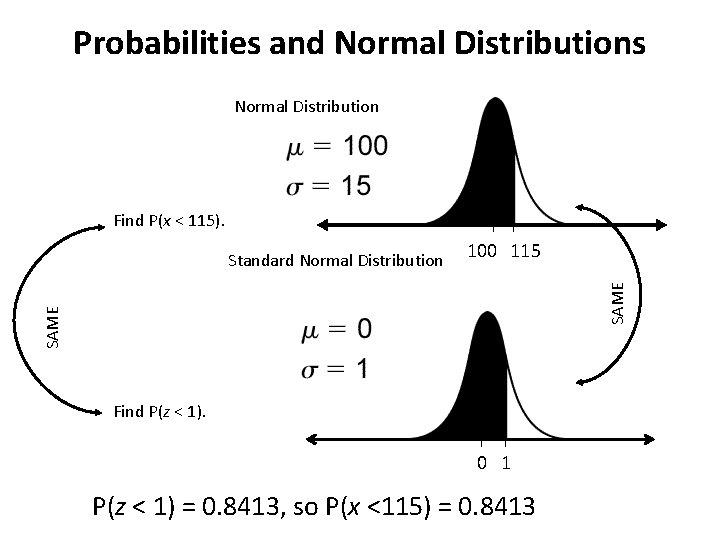
Probabilities and Normal Distributions Normal Distribution Find P(x < 115). 100 115 SAME Standard Normal Distribution Find P(z < 1). 0 1 P(z < 1) = 0. 8413, so P(x <115) = 0. 8413

Application Monthly utility bills in a certain city are normally distributed with a mean of $100 and a standard deviation of $12. A utility bill is randomly selected. Find the probability it is between $80 and $115. Normal Distribution P(80 < x < 115) P(– 1. 67 < z < 1. 25) 0. 8944 – 0. 0475 = 0. 8469 The probability a utility bill is between $80 and $115 is 0. 8469.

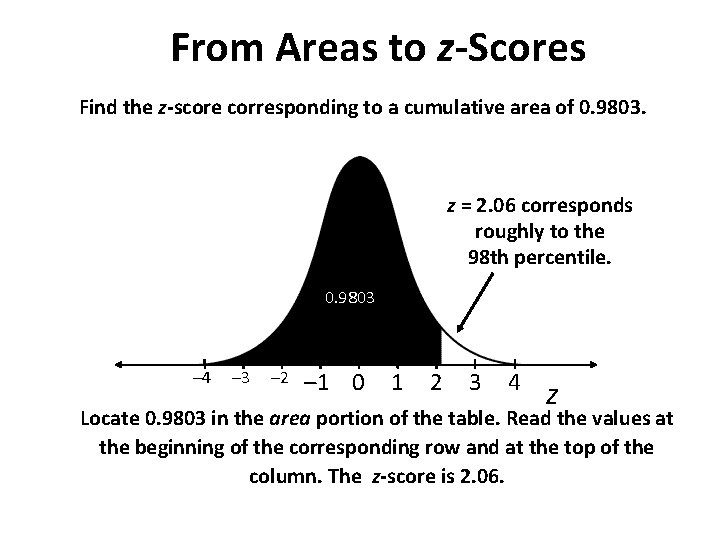
From Areas to z-Scores Find the z-score corresponding to a cumulative area of 0. 9803. z = 2. 06 corresponds roughly to the 98 th percentile. 0. 9803 – 4 – 3 – 2 – 1 0 1 2 3 4 z Locate 0. 9803 in the area portion of the table. Read the values at the beginning of the corresponding row and at the top of the column. The z-score is 2. 06.

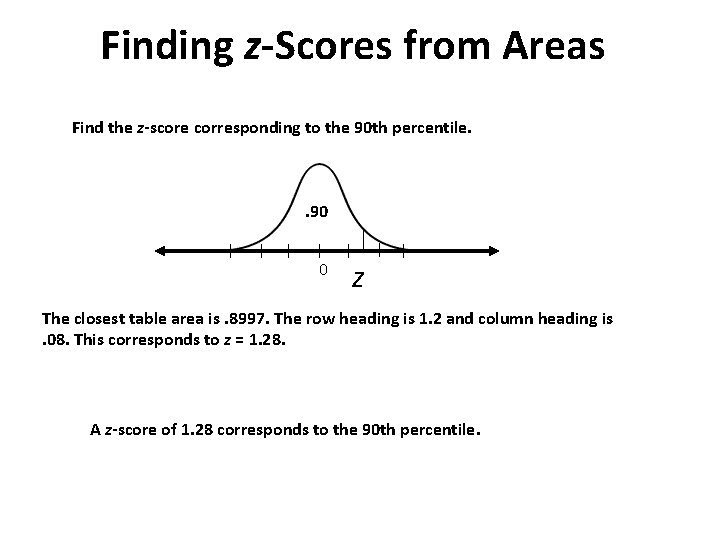
Finding z-Scores from Areas Find the z-score corresponding to the 90 th percentile. . 90 0 z The closest table area is. 8997. The row heading is 1. 2 and column heading is. 08. This corresponds to z = 1. 28. A z-score of 1. 28 corresponds to the 90 th percentile.

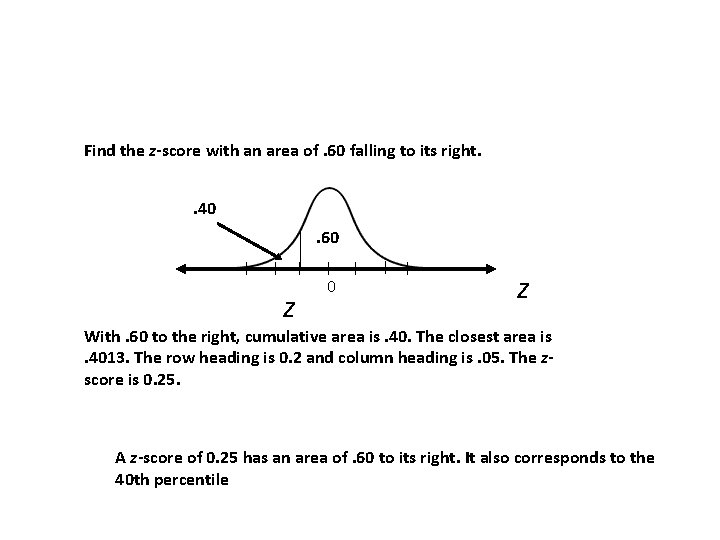
Finding z-Scores from Areas Find the z-score with an area of. 60 falling to its right. . 40. 60 z With. 60 to the right, cumulative area is. 40. The closest area is. 4013. The row heading is 0. 2 and column heading is. 05. The zscore is 0. 25. A z-score of 0. 25 has an area of. 60 to its right. It also corresponds to the 40 th percentile

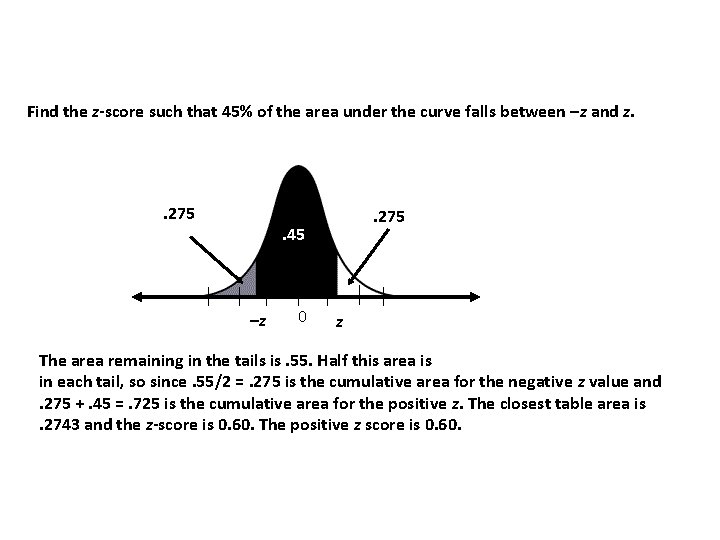
Finding z-Scores from Areas Find the z-score such that 45% of the area under the curve falls between –z and z. . 275 . 45 –z 0 z The area remaining in the tails is. 55. Half this area is in each tail, so since. 55/2 =. 275 is the cumulative area for the negative z value and. 275 +. 45 =. 725 is the cumulative area for the positive z. The closest table area is. 2743 and the z-score is 0. 60. The positive z score is 0. 60.

From z-Scores to Raw Scores To find the data value, x when given a standard score, z: The test scores for a civil service exam are normally distributed with a mean of 152 and a standard deviation of 7. Find the test score for a person with a standard score of: (a) 2. 33 (b) – 1. 75 (c) 0 (a) x = 152 + (2. 33)(7) = 168. 31 (b) x = 152 + (– 1. 75)(7) = 139. 75 (c) x = 152 + (0)(7) = 152

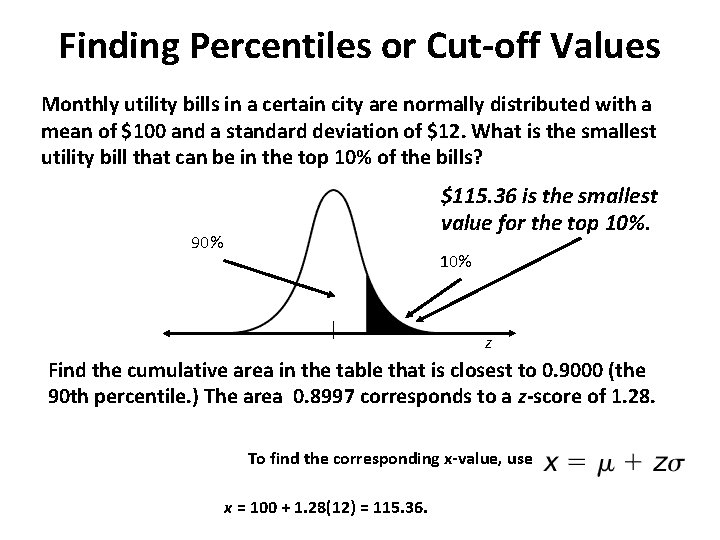
Finding Percentiles or Cut-off Values Monthly utility bills in a certain city are normally distributed with a mean of $100 and a standard deviation of $12. What is the smallest utility bill that can be in the top 10% of the bills? $115. 36 is the smallest value for the top 10%. 90% 10% z Find the cumulative area in the table that is closest to 0. 9000 (the 90 th percentile. ) The area 0. 8997 corresponds to a z-score of 1. 28. To find the corresponding x-value, use x = 100 + 1. 28(12) = 115. 36.

Homework : 1 -37 (odd) pgs. 242 -243 42 -46 even pgs. 243 -244. Day 2: Homework : 2 -36 (even) pgs. 242 -243 41 -45 odd pgs. 243 -244.