Section 5 1 Slope A rate of change

Section 5 -1 Slope

A rate of change is a ratio that compares the amount of change in a dependent variable to the amount of change in an independent variable. (y ) (x ) For any two points on a nonvertical line, this ratio is constant. The constant rate of change of a nonvertical line is called the slope of the line.

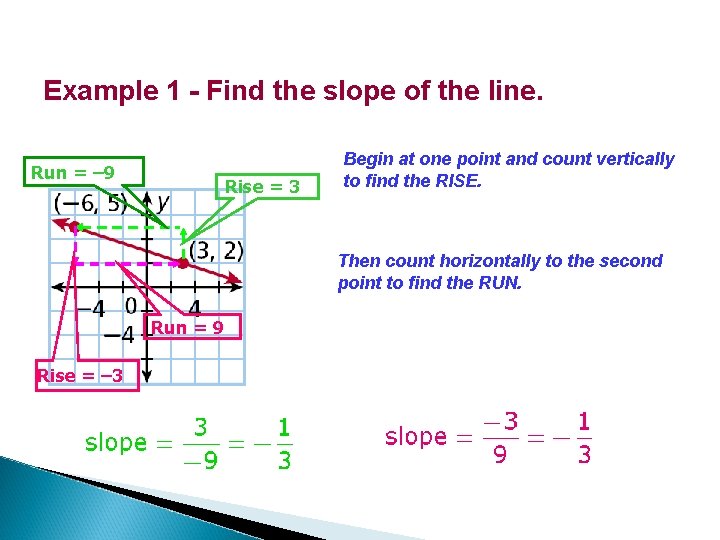
Example 1 - Find the slope of the line. Run = – 9 Rise = 3 Begin at one point and count vertically to find the RISE. Then count horizontally to the second point to find the RUN. Run = 9 Rise = – 3

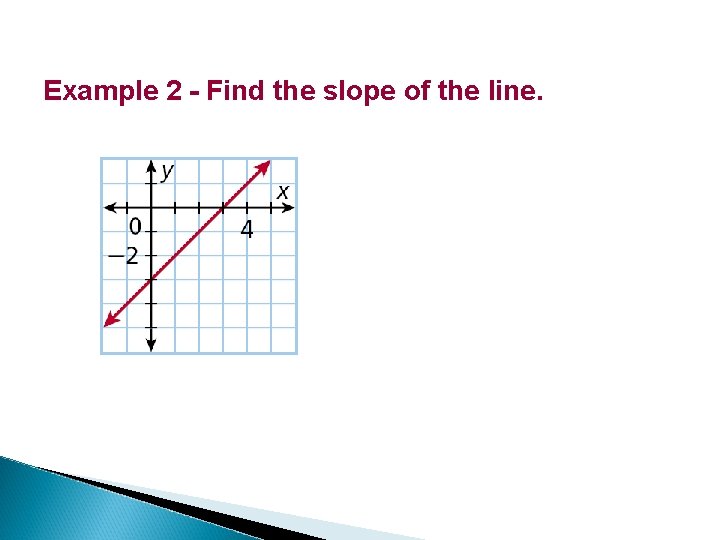
Example 2 - Find the slope of the line.

If you know 2 different points on a line, you can use the slope formula to find the slope of the line. RISE RUN

Reading Math The small numbers to the bottom right of the variables are called subscripts. Read x 1 as “x sub one” and y 2 as “y sub two. ”

Example 3 – Find the slope Example 4 – Find the slope between the points (5, 4) and between the points (3, -2) (-1, 12). and (-5, -7).

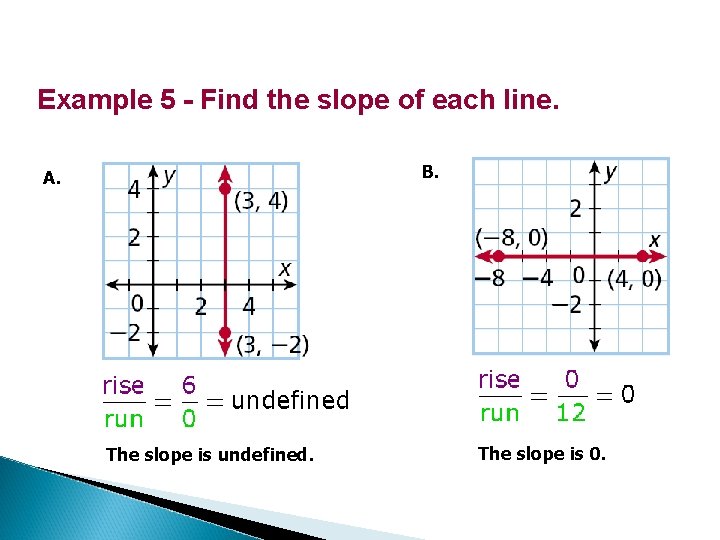
Example 5 - Find the slope of each line. B. A. The slope is undefined. The slope is 0.

Example 6 - Find the slope of the line that contains (– 2, – 2) and (7, – 2). Substitute (– 2, – 2) for (x 1, y 1) and (7, – 2) for (x 2, y 2).

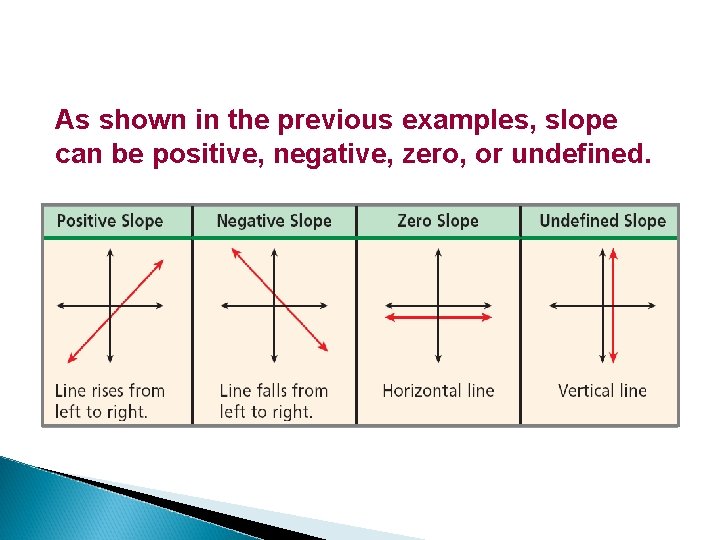
As shown in the previous examples, slope can be positive, negative, zero, or undefined.

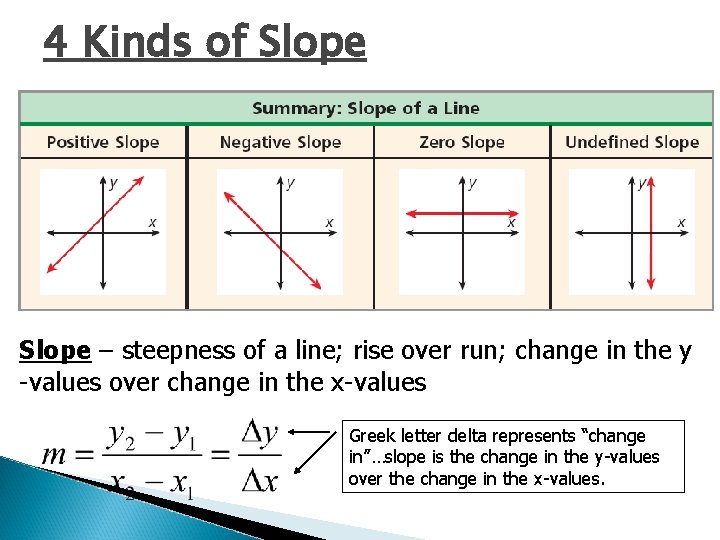
4 Kinds of Slope – steepness of a line; rise over run; change in the y -values over change in the x-values Greek letter delta represents “change in”…slope is the change in the y-values over the change in the x-values.

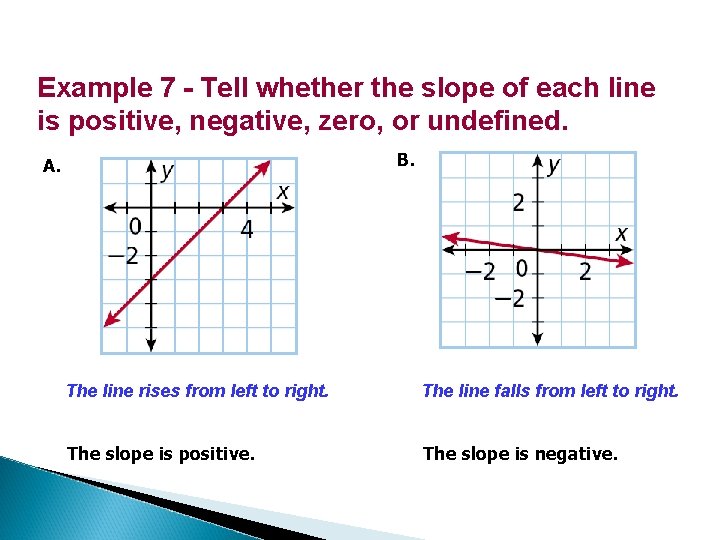
Example 7 - Tell whether the slope of each line is positive, negative, zero, or undefined. B. A. The line rises from left to right. The line falls from left to right. The slope is positive. The slope is negative.

Example 8 - Tell whether the slope of each line is positive, negative, zero, or undefined. c. The line is vertical. d. The line rises from left to right. The slope is undefined. The slope is positive.

Remember that slope is a rate of change. In real-world problems, finding the slope can give you information about how a quantity is changing.

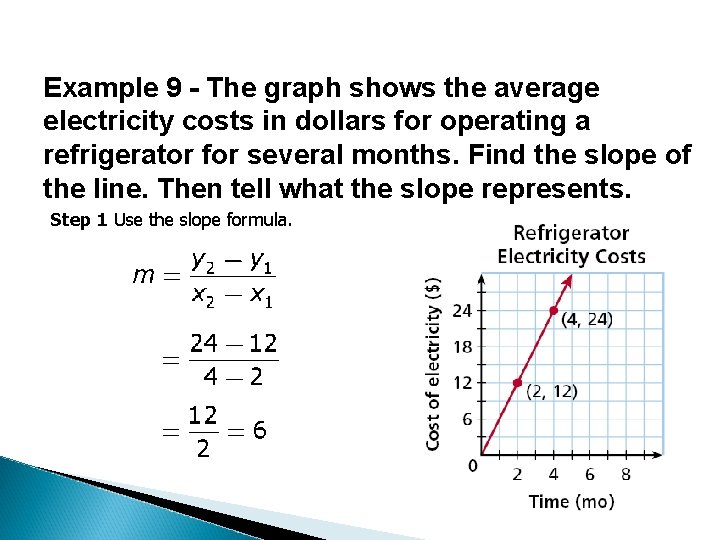
Example 9 - The graph shows the average electricity costs in dollars for operating a refrigerator for several months. Find the slope of the line. Then tell what the slope represents. Step 1 Use the slope formula.

Example 9 Continued Step 2 Tell what the slope represents. In this situation, y represents the total cost of electricity and x represents time. So slope represents in units of . A slope of 6 means that the cost of electricity to run the refrigerator is increasing (positive change) at a rate of 6 dollars each month.

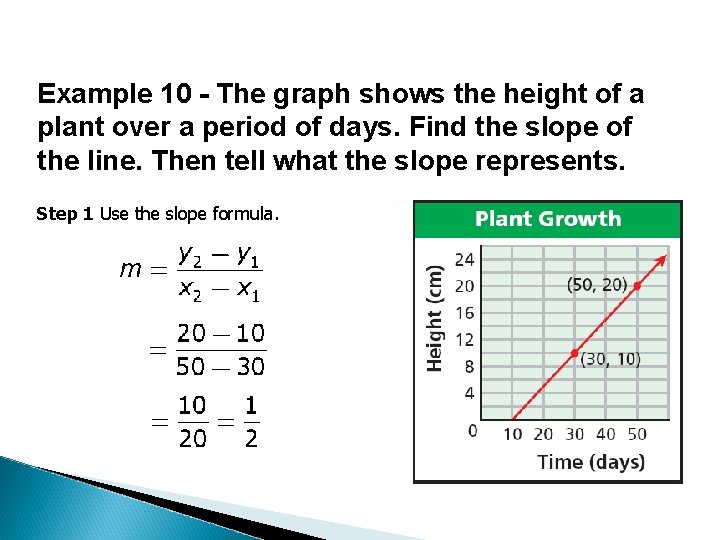
Example 10 - The graph shows the height of a plant over a period of days. Find the slope of the line. Then tell what the slope represents. Step 1 Use the slope formula.

Example 10 Continued Step 2 Tell what the slope represents. In this situation, y represents the height of the plant and x represents time. So slope represents in units of . A slope of means that the height of the plant is increasing (positive change) at a rate of 1 cm every two days.

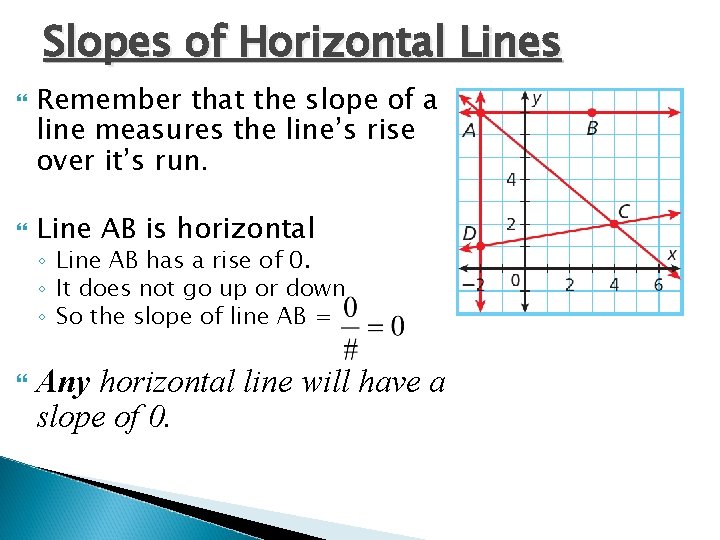
Slopes of Horizontal Lines Remember that the slope of a line measures the line’s rise over it’s run. Line AB is horizontal ◦ Line AB has a rise of 0. ◦ It does not go up or down ◦ So the slope of line AB = Any horizontal line will have a slope of 0.

Slopes of Vertical Lines Remember that the slope of a line measures the line’s rise over it’s run. Line AD is a vertical line. ◦ Line AD has a run of 0. ◦ It does not go left or right ◦ So the slope of line AD = Any vertical line will have a slope that is undefined.

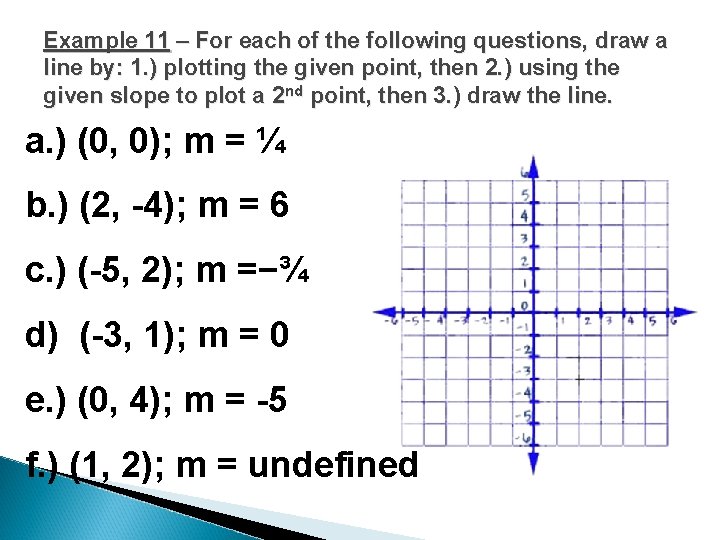
Example 11 – For each of the following questions, draw a line by: 1. ) plotting the given point, then 2. ) using the given slope to plot a 2 nd point, then 3. ) draw the line. a. ) (0, 0); m = ¼ b. ) (2, -4); m = 6 c. ) (-5, 2); m =−¾ d) (-3, 1); m = 0 e. ) (0, 4); m = -5 f. ) (1, 2); m = undefined

Finding the missing coordinate when given the slope. Example – Find the value of r so that the line through (– 3 , 9) and (r, 6) has a slope of ¾.

Example 12 – Find the value of r so that the line through (-1, -2) and (-4, r) has a slope of -1. CHECK: 1(r + 2) = -1(-3) r+2=3 r=1

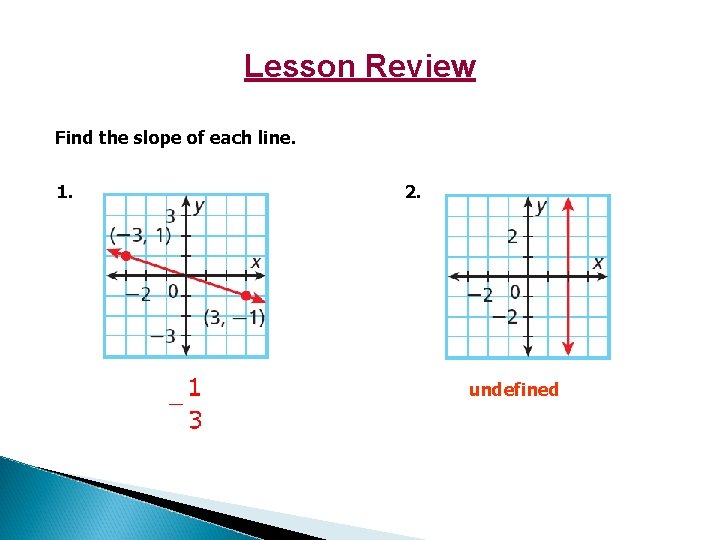
Lesson Review Find the slope of each line. 1. 2. undefined

Lesson Review 3. Find the slope of the line that contains (5, 3) and (– 1, 4). 4. Find the slope. Then tell what the slope represents. Slope = 50 A slope of 50 means that the speed of the bus is 50 mi/h.

Assignment Skills Practice 5 -1 (In-Class) Pages 260– 261 #’s 16– 32 (evens), 39, 41– 44, 49, 53– 55. (Homework)