Section 5 1 Hypothesis Tests Using Normal Distributions

Section 5. 1 Hypothesis Tests Using Normal Distributions Statistics: Unlocking the Power of Data Lock 5

Randomization Distributions If a randomization distribution is normally distributed, we can write it as a) N(null value, se) b) N(statistic, se) c) N(parameter, se) Statistics: Unlocking the Power of Data Lock 5

Normal Distribution Which normal distribution should we use to approximate this? Statistics: Unlocking the Power of Data a) N(0, -0. 131) b) N(0, 0. 056) c) N(-0. 131, 0. 056) d) N(0. 056, 0) Lock 5

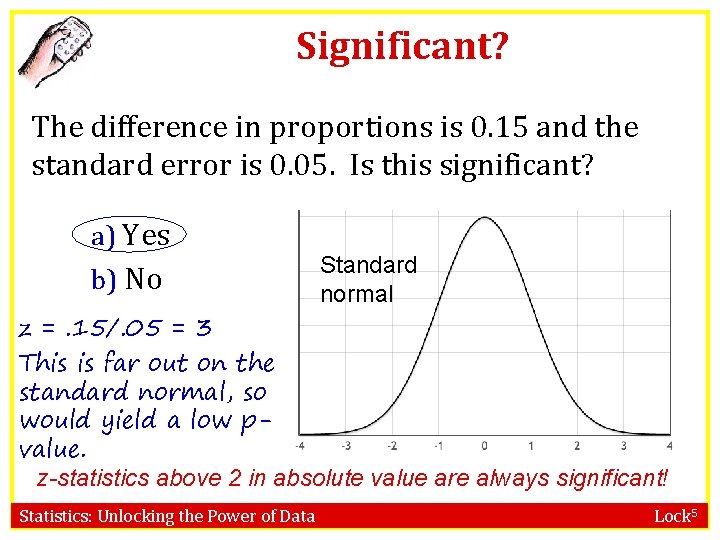
Significant? The difference in proportions is 0. 15 and the standard error is 0. 05. Is this significant? a) Yes b) No Standard normal z =. 15/. 05 = 3 This is far out on the standard normal, so would yield a low pvalue. z-statistics above 2 in absolute value are always significant! Statistics: Unlocking the Power of Data Lock 5

First Born Children Statistics: Unlocking the Power of Data Lock 5

z-statistic If z = – 3, using = 0. 05 we would (a) Reject the null (b) Not reject the null (c) Impossible to tell (d) I have no idea About 95% of z-statistics are within -2 and +2, so anything beyond those values will be in the most extreme 5%, or equivalently will give a p-value less than 0. 05. Statistics: Unlocking the Power of Data Lock 5

Section 5. 2 Confidence Intervals Using Normal Distributions Statistics: Unlocking the Power of Data Lock 5

Review The Central Limit Theorem applies to the distribution of the a) statistic b) parameter c) null value d) data e) standard error Statistics: Unlocking the Power of Data Lock 5

Bootstrap Distributions If a bootstrap distribution is approximately normally distributed, we can write it as a) b) c) d) N(parameter, sd) N(statistic, sd) N(parameter, se) N(statistic, se) sd = standard deviation of variable se = standard error = standard deviation of statistic Statistics: Unlocking the Power of Data Lock 5

Bootstrap Distribution A bootstrap distribution is approximated by the normal distribution N(0. 15, 0. 03). What is the standard error of the statistic? a) 0. 15 b) 0. 3 c) 0. 03 d) 0. 06 N(mean, sd) The sd of a bootstrap distribution is the standard error of the statistic. Statistics: Unlocking the Power of Data Lock 5

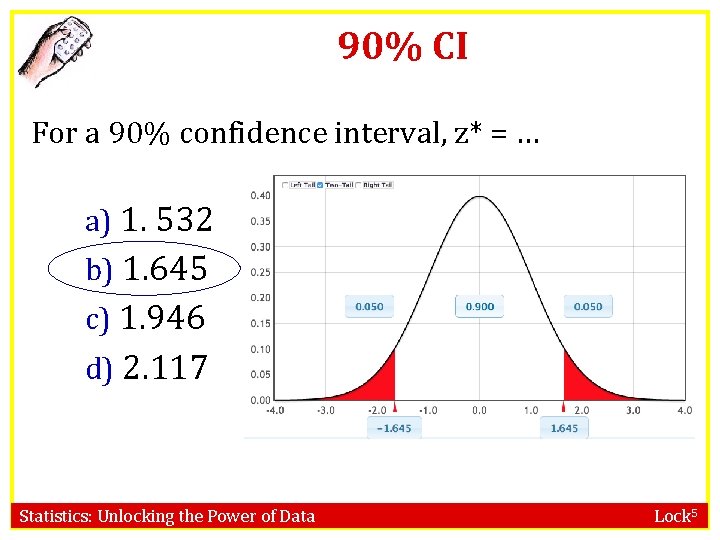
90% CI For a 90% confidence interval, z* = … a) 1. 532 b) 1. 645 c) 1. 946 d) 2. 117 Statistics: Unlocking the Power of Data Lock 5

Hearing Loss • In a random sample of 1771 Americans aged 12 to 19, 19. 5% had some hearing loss (this is a dramatic increase from a decade ago!). The standard error for this sample proportion is 0. 0095. • What proportion of Americans aged 12 to 19 have some hearing loss? Give a 99% CI. • What is z* for this confidence interval? A. 0. 99 B. 0. 195 C. 1. 960 D. 1. 645 E. 2. 575 Rabin, R. “Childhood: Hearing Loss Grows Among Teenagers, ” www. nytimes. com, 8/23/10. Statistics: Unlocking the Power of Data Lock 5

Hearing Loss 19. 5% of the sample had some hearing loss and the standard error is 0. 0095. A 99% confidence interval for the proportion of Americans aged 12 -19 with some hearing loss is: A. 0. 156 to 0. 235 B. 0. 171 to 0. 219 C. 0. 185 to 0. 205 D. 0. 193 to 0. 197 statistic z* SE 0. 195 2. 575 0. 0095 (0. 171, 0. 219) Statistics: Unlocking the Power of Data Lock 5