SECTION 5 1 DATA PRODUCTION AND DESIGNING SAMPLES

SECTION 5. 1 DATA PRODUCTION AND DESIGNING SAMPLES

WHY IS RANDOMNESS IMPORTANT IN STATISTICAL RESEARCH? Randomness gives everyone in the population an equal chance of being selected Goal: create a sample that is representative of the population Note: generating random numbers that are truly random is very difficult, computers near impossible When selecting a sample, we need to avoid any bias in our selection In this course, to select random values we use the Random digits table “B”

Q: Why we need the random digits table? a) We suck at making up random digits b) Humans are not a good judge of randomness c) We need procedures to follow to ensure randomization, which is key in sampling and experimentation. d) All of the above e) None of the above In this chapter we will look at how Collection/Production of “good” data requires careful planning Garbage in, garbage, out; if data is collected badly, outcomes are meaningless

OBSERVATIONAL VS EXPERIMENTAL Observational Study Observes individuals and measures variables of interest but does not attempt to influence the response Only observe and record, does NOT manipulate anything no control over any treatments the subject may be given or which groups the subjects may be separated into Ie: surveys, political polls, Nielsen ratings (TV or radio), Experiment Deliberately imposes some treatment on individuals in order to observe their response Identifies certain causes and effect relationships among the variables in the study. Ie: FDA drug/clinical trials, marshmallow experiment, sdf

Ex: Indicate if the following is an experiment or observation. Explain why. i) To determine the effects of a drug, the sample is divided in half. One half received the drug daily, the other received a placebo Experiment subjects assigned diet, theirthe treatment ii) To determine the effects– of eating are a vegetarian researchers sets out to find two groups: 1 st group 100 vegetarians, 2 nd group 100 meat eaters. Observational – subjects were found, iii) A group of students were studied to not findassigned the correlation between watching tv and school grades. One group is assigned to 4 hours per day. The other is assigned to less than 1 hour per day. iv) A study was conducted on the impact of over-drinking on self confidence. Three samples were made. how Themany 1 st group were heavy Experimental – students were assigned hours of tv drinkers. 2 nd: Mild, 3 rd: Rare. Observational – people were not assigned how much to drink

WHICH OF THE FOLLOWING IS AN ADVANTAGE TO USING SURVEYS AS OPPOSED TO EXPERIMENTS? a) Surveys are more ethically correct than experiments b) Surveys are generally cheaper than experiments c) It is generally easier to conclude cause and effect from surveys than experiments d) Surveys involves the use of randomization e) Surveys are less bias than experiments Answer: B Surveys are generally cheaper and quicker to conduct than experiments. C is wrong b/c it is very difficult to conclude cause & effect from surveys. Experiments also involves randomization, ie: random assignments of groups to treatments. Surveys are subject to bias and unethical practices, ie: manipulating response with use of wording.

POPULATION AND SAMPLES Population The entire group of individuals (not necessarily people) we want information about. Sample Part of the population in the study Census: Information is collected regarding everyone A small group from this population will be selected to create a sample. The sample must be unbias and fair Population: 23, 000 people

Ex: Identify the population as exactly as possible. That is, say what kind of individuals the population consists of and say exactly which individuals fall in the population. a) The Vancouver Sun surveys 1500 UBC students for the University’s opinion on the use of natural resources. Individual: a single UBC student Population: all UBC students b) The Ministry of Education conducts a survey on the use of technology in the classroom of BC high schools Individual: a single classroom Population: all classrooms in BC highschools c) The juice boxes in a local factory are assessed to meet government standards. A sample of 5 juice boxes are taken from a shipment of 1000 boxes. Individual: a juice box Population: all 1000 juices boxes from the shipment

DATA COLLECTION: Sampling Studies a part in order to gain information about the whole The method we use to select the sample is called the “sample design”. Convenience Sampling, Voluntary Sampling, SRS, stratified, cluster, multistage sampling Census Attempts to contact every individual in the entire population.

EXAMPLES OF BIAS SAMPLES/BAD SAMPLING Convenience Sampling Taking a sample from individuals who are easiest to reach ie: Asking spectators in a hockey game what they favourite sport is Problem: Sample may not be diverse enough to accurately represent all students Voluntary Response Sampling Sample is taken from people who volunteer themselves ie: We post an advertisement in the newspaper asking students to respond. Problem: People with strong opinions (often strong negative opinions) tend to reply, so they are over-represented

Voluntary Response and Convenience sampling results in a sample that is not representative of the population. Sample is bias and favour certain outcomes. Having a random sample selection eliminates bias Ex: Indicate which ones are “Voluntary” or “Convenience” Sampling: Voluntary a) Phone in Surveys b) Surveying in the shopping mall c) Election polls Convenience Voluntary d) Surveying people at a cruise Convenience e) Radio or TV shows where people call in Voluntary

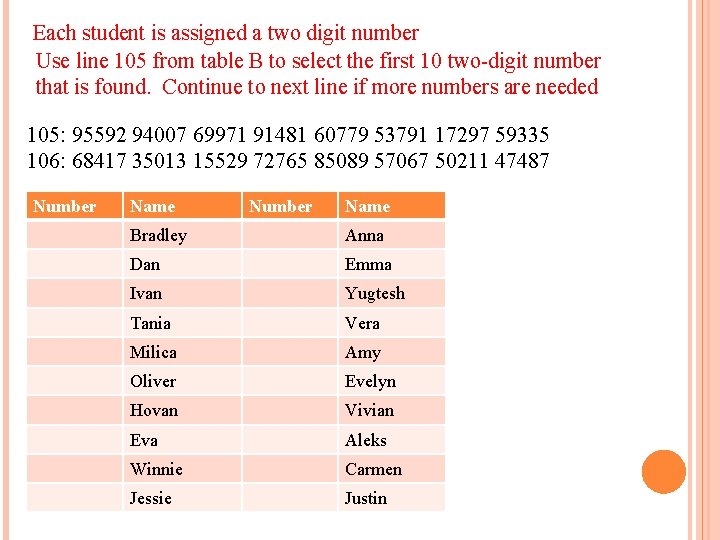
SIMPLE RANDOM SAMPLE (SRS) All individuals are equally likely to be selected for the sample All groups of “n” individuals are equally likely to be chosen Names of everyone in the population in a list Use a table of random digits to select the sample Table of Random Digits (Table B) – back of book OR TI-83 - Math/PRB/5: rand. Int(lower, upper, [numtrials]) Example: 10 students from Mr. Young’s class will be selected for a sample. Use line 105 in table B to select a random sample of 10 students

Each student is assigned a two digit number Use line 105 from table B to select the first 10 two-digit number that is found. Continue to next line if more numbers are needed 105: 95592 94007 69971 91481 60779 53791 17297 59335 106: 68417 35013 15529 72765 85089 57067 50211 47487 Number Name Bradley Anna Dan Emma Ivan Yugtesh Tania Vera Milica Amy Oliver Evelyn Hovan Vivian Eva Aleks Winnie Carmen Jessie Justin

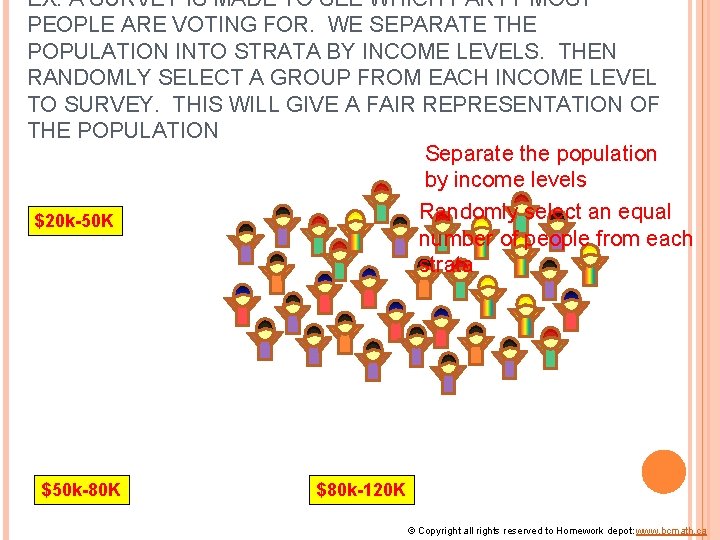
STRATIFIED SAMPLING Divide the population into subgroups or stratas, depending on the characteristic of the groups (income, grade level, schools, etc. ). Then take a simple random sample from each strata All selected individuals are combined to create your sample Gives a fair representation to each subgroup Q: Is stratified sampling a type of SRS? Ex: A survey is made to see which party most people are voting for. We separate the population into strata by income levels. Then randomly select a group from each income level to survey. © Copyright all rights reserved to Homework depot: www. bcmath. ca

EX: A SURVEY IS MADE TO SEE WHICH PARTY MOST PEOPLE ARE VOTING FOR. WE SEPARATE THE POPULATION INTO STRATA BY INCOME LEVELS. THEN RANDOMLY SELECT A GROUP FROM EACH INCOME LEVEL TO SURVEY. THIS WILL GIVE A FAIR REPRESENTATION OF THE POPULATION Separate the population by income levels Randomly select an equal $20 k-50 K number of people from each strata $50 k-80 K $80 k-120 K © Copyright all rights reserved to Homework depot: www. bcmath. ca

CLUSTER SAMPLING The population is divided into smaller groups known as “clusters” Out of the many clusters, a few are randomly selected to create a sample Everyone in the selected clusters will be part of the sample Q: What is the difference btn Cluster and Stratified? Ex: A study on tooth decay is conducted in B. C. high schools. A random sample is to be created using cluster sampling. All the schools are divided into clusters and a few schools are chosen for the sample © Copyright all rights reserved to Homework depot: www. bcmath. ca

EX: YOU WANT TO FIND OUT ABOUT TOOTH DECAY IN B. C. HIGH SCHOOL. YOU CHOOSE TO USE SCHOOLS AS YOUR CLUSTERS. THEN YOU A FEW SCHOOLS OUT OF THE TOTAL SCHOOLS AND SURVEY ALL THE STUDENTS IN THOSE SCHOOLS Randomly select a few schools or “clusters” Then all the students in these schools will be selected for the sample © Copyright all rights reserved to Homework depot: www. bcmath. ca

MULTISTAGE SAMPLING Select several groups; within each group, select a subgroup; within each subgroup select individuals for the sample. Example: Select several departments within the school (Math, English, Art) Within each of those departments, select several teachers. Choose several student within each class

Q: Each of the 40 teams in a league has a 50 players each. A sample of 80 players is to be randomly selected to undergo steroid testing. To select this sample, each team is instructed to put their 40 names in a hat and randomly draw two names. Will this method result in a SSR of the 2000 players in the league? a) Yes, because each player has the same chance of being selected b) Yes, because each team is equally represented c) Yes, because this is an example of stratified sampling, which is a special case of SSR d) No, because the teams are not chosen randomly e) No, because not each group of 80 players has the same chance of being selected Answer: E, in a SSR, every possible group of 80 players must be equally likely. This is not the case here b/c you can’t have a group of 80 players all from the same team. This is an example of Stratified sampling, not the same as SSR

Q: Telus plans to introduce a new telephone service for its customers. They selects a large number of clients from their database to survey regarding their opinion. What type of sampling is this? a) Cluster, because they are only surveying their customers b) Simple Random Sample, because every customer is equally likely to be chosen c) Stratified, because they are selecting customers within BC d) Convenience, because they are only selecting customers within their database e) Systematic, because they would use a system to select from their database Answer: Convenience, they are selecting ppl that are easy to reach within their database. The data will not be representative of the entire population. The result of this data will not tell us what ppl outside of their consumer base would think of the new service

PROBLEMS WITH SAMPLE SURVEYS All sampling methods mentioned aim to minimize bias by using chance/probability Undercoverage Some groups are left out in the process of choosing a sample (homeless people, students) Excluding certain groups (children) Non-response Individuals chosen cannot be contacted or don’t cooperate Response Bias Respondents may lie or try to guess what the interviewer wants to hear Wording of Questions Confusing/misleading questions

WORDING OF QUESTIONS Confusing or leading questions influence response; poorly worded questions will not yield accurate responses. Example 1: “In a recent study, students in an Algebra 1 course were given a 25 question basic skills test. On average, students used a graphing calculator to answer 21 out of 25 questions. Do you think graphing calculators are overused? Example 2: By using a graphing calculator, students in Algebra 1 course were able to make visual connection between equations and their graphs, reinforcing difficult concepts. Do you think graphing calculators are overused? Each question gives only one side of an issue. Thus creates a bias response.

INFERENCES ABOUT THE POPULATION Each time a sample is taken, it’s makes an estimate of the population Every sample is different but the population is consistent Using chance and probability methods to generate a sample will reduce systematic bias and allow better inferences of the population Larger random samples gives more accurate results than smaller samples reducing the margin of error

QUESTIONS TO ASK YOURSELF BEFORE YOU BELIEVE A POLL/SURVEY. . . Who carried out the survey? How was the sample selected? How large was the sample? What was the response rate? How were the subjects contacted? When was the survey conducted? What was the exact question asked?

Ex: A newspaper article about an opinion poll says that “ 43% of Americans approve of the president’s overall job performance. ” Toward the end of the article, your read: “The poll is based on telephone interviews with 1210 adults from around the United States, excluding Alaska and Hawaii. ” What variable did this poll measure? What population do you think the newspaper wants information about? What was the sample? Are there any sources of bias in the sampling method used? Variable: Approval of president’s performance Population: Adults citizens of the US or registered voters Sample: 1210 adults interviewed Possible sources of bias: Only adults with phones were contacted. Alaska and Hawaii were omitted.

A large company wants to conduct a survey on the level of career satisfaction from its employees. The company has 1470 employees and a questionnaire is to be sent to a SRS of 100 employees. Describe how you will select the sample. Follow the four steps: label; table; stopping rule; and identify sample. Assign every employee a four digit number from 0001 to 1470 in alphabetical order. Omit numbers like 0000 and from 1471 to 9999 Use table B and randomly select a row to generate random 4 digit numbers. Continue the process unit you have 100 names

HW: P 333 1 -8 P 341 9 -14 P 347 15 – 20 P 350 26 - 32