Section 5 1 CHAPTER 5 WORK AND ENERGY

Section 5 -1 CHAPTER 5 WORK AND ENERGY

Work – Section 5 -1 Definition of Work Ordinary Definition : To us, WORK means to do something that takes physical or mental effort. ◦ Ex: Holding a Chair at Arm’s Length for several Minutes Scientific Definition : In Physics, WORK is ONLY done when a force causes an object to be displaced (move). Ex : Pushing a chair from one side of the room to the other. There are three key words in this definition - force, displacement, and cause. In order for a force to qualify as having done work on an object, there must be a displacement and the force must cause the displacement.

� Work is done ONLY when components of a force are parallel to or at an angle (not 90 degrees) to the displacement. Ex: Push Chair Horizontally, only horizontal component of force � Components of the force perpendicular to a displacement do NOT do work. �Ex: If you are exerting force to move an object horizontally, vertical force will not do work on the object.

Work Formula W = Fd(cos angle) Work = Force x displacement x cosine of angle between them. If angle = 0 degrees, cosine of 0 degrees = 1 so we can use W = Fd If angle = 90 degrees, cosine of 90 degrees = 0 and W = 0. ◦ No work is done on a bucket of water being carried by a student walking horizontally. (Upward force is perpendicular to the displacement of the bucket).

Example Let's consider the force of a chain pulling upwards and rightwards upon Fido in order to drag Fido to the right. It is only the horizontal component of the tensional force in the chain which causes Fido to be displaced to the right. The horizontal component is found by multiplying the force F by the cosine of the angle between F and d. In this sense, the cosine theta in the work equation relates to the cause factor - it selects the portion of the force which actually causes a displacement.

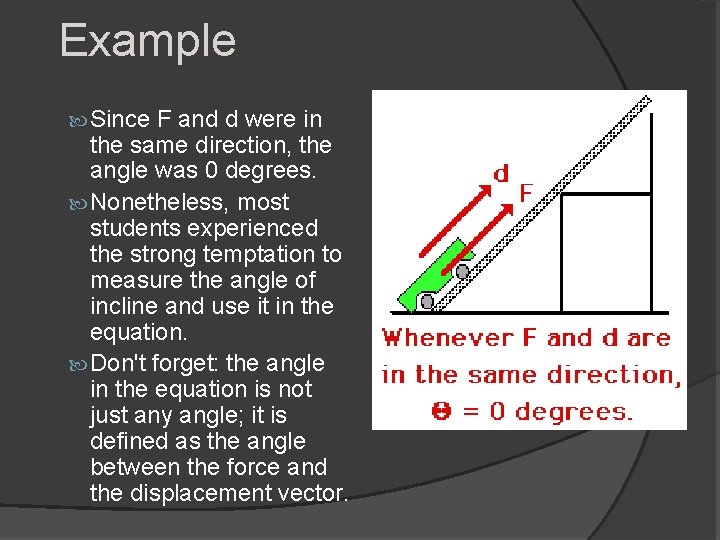
Example Since F and d were in the same direction, the angle was 0 degrees. Nonetheless, most students experienced the strong temptation to measure the angle of incline and use it in the equation. Don't forget: the angle in the equation is not just any angle; it is defined as the angle between the force and the displacement vector.

Units of Work � Work has dimensions of Force and Length. � In SI system, work has a unit of newtons times meters (N*m) or Joules (J). ex: Work done lifting an apple from your waist to the top of your head is about 1 J. Three push ups require about 1, 000 J.

The sign of work is Important. � Work is a scalar quantity. � Work can be positive or negative. � Work is positive when the component force is in the same direction of displacement. � Ex: when you lift a box, work done is positive because the force is upward and the box is moving upward. � Work is negative when the force is in the direction opposite the displacement. � Ex: Force of kinetic friction between sliding box and the floor is opposite the displacement of the box.

Guided Practice � Pg. 169 Sample 5 A

CHAPTER 5 WORK AND ENERGY Section 2 Energy Kinetic Energy Work-Kinetic Energy Theorem

Different forms of Energy � Energy has a number of different forms, all of which measure the ability of an object or system to do work on another object or system. � In Chapter 5 we will learn about the following types of energy: - Kinetic Energy - Potential Energy - Gravitational Potential Energy - Elastic Potential Energy - Mechanical Energy

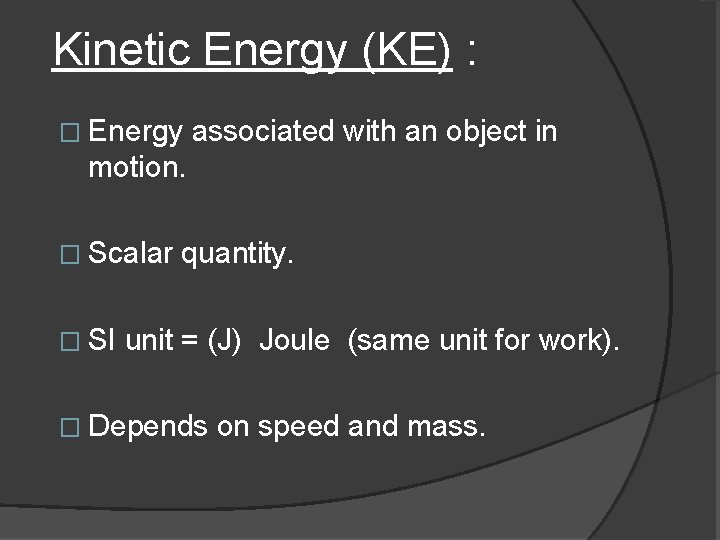
Kinetic Energy (KE) : � Energy associated with an object in motion. � Scalar � SI quantity. unit = (J) Joule (same unit for work). � Depends on speed and mass.

Formula for Kinetic Energy �KE = ½ m v 2 �Kinetic Energy = ½ x mass x (speed)2 �Kinetic Energy depends on BOTH an object’s speed and mass.

Let’s Practice some problems… � Open your books to pg. 173 and work sample problem 5 B

Work-Kinetic Energy Theorem � Net work done by a Net Force acting on an object is equal to the change in the kinetic energy of the object. � Net work = change in kinetic energy = Δ KE �Wnet = KEf - KEi �Fnet d(cos θ) = ½ mv 2 f – ½ mv 2 i �Wnet

Fnet these problems, Fnet means the net force doing the work. � In � Using our Work-Kinetic Energy Theorem our Fnet can mean : ○ Friction Force (Remember Ff = μFn ) ○ Constant Force ○ Forward Force Minus Resistive force

Section 3 Conservation of Mechanical Energy CHAPTER 5 WORK AND ENERGY

Conservation of Energy � Energy can never be lost. It can only change form. Energy is a conserved quantity. � When something is conserved, it remains constant. � The form of a conserved quantity can change, but we will always have the same amount. � Mass is an example of a conserved quantity.

Conserved Quantity The mass of the light bulb whether whole or in pieces is constant and thus conserved.

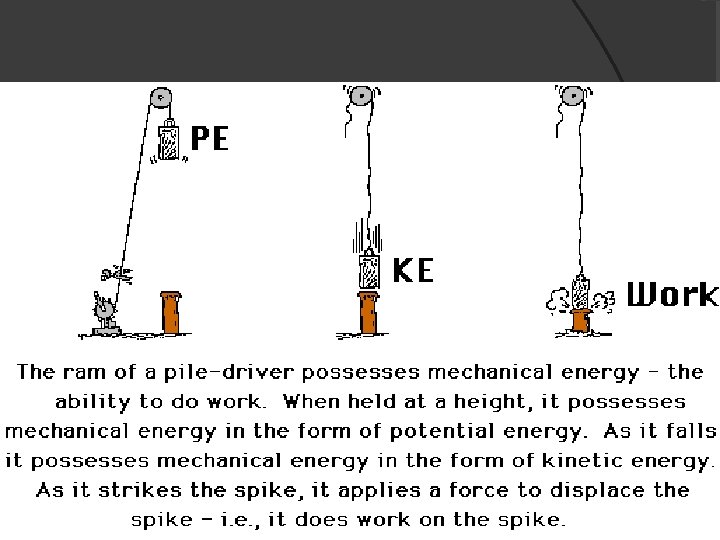
Mechanical Energy � Can be either kinetic energy (energy of motion) or potential energy (stored energy of position). � Is the sum of kinetic energy and all forms of potential energy of an object or group. � Is not conserved in the presence of friction.

Mechanical Energy � Is conserved only in the absence of friction. � When there is no friction, mechanical energy can be conserved. � This principle is called Conservation of Mechanical Energy: �MEi = MEf �Initial Mechanical Energy = Final Mechanical Energy

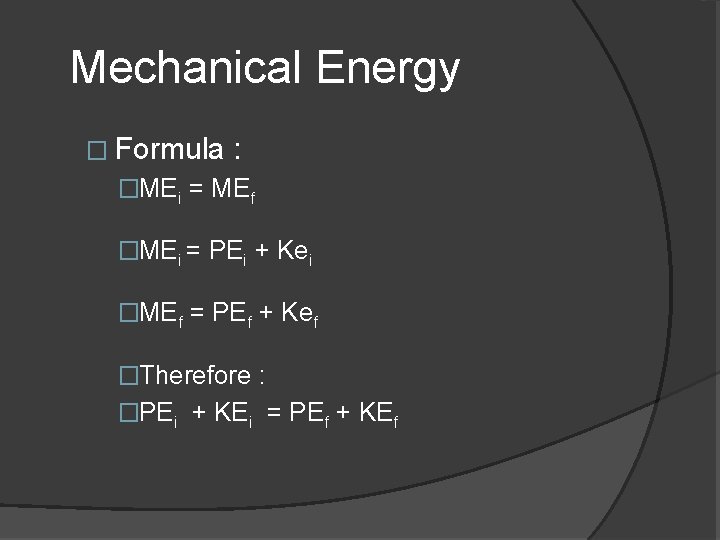
Mechanical Energy � Formula : �MEi = MEf �MEi = PEi + Kei �MEf = PEf + Kef �Therefore : �PEi + KEi = PEf + KEf

Practice Problem � Pg. 184 Sample Problem 5 E

Section 4 Power CHAPTER 5 WORK AND ENERGY

Power � The rate at which work is done. � Rate of energy transfer by any method. � Machines with different power ratings do the same work in different time intervals. � The more power you have, the faster your work will get done.

Formulas for Power �P = Fv � Power �P = force x speed = Wk / t � Power = Work / Time

Units for Power � SI Unit = Watt (W) � Watt = 1 Joule/second � Horsepower (hp) is another unit of power. � 1 hp = 746 W

Practice Problem �How long does it take a 19 k. W steam engine to do 6. 8 x 10^7 J of work?