Section 5 1 Bisectors in Triangles Objectives Then

Section 5 -1 Bisectors in Triangles
Objectives Then Now You used segment and angle bisectors. Identify and use perpendicular bisectors in triangles. Identify and use angle bisectors in triangles.

Content Standards Common Core State Standards G. CO. 10 – Prove theorems about triangles. G. MG. 3 – Apply geometric methods to solve problems. Mathematical Practices 1) Make sense of problems and persevere in solving them. 3) Construct viable arguments and critique the reasoning of others.

Perpendicular Bisector: A bisector that is also perpendicular to a segment. Vocabulary

Perpendicular Bisectors
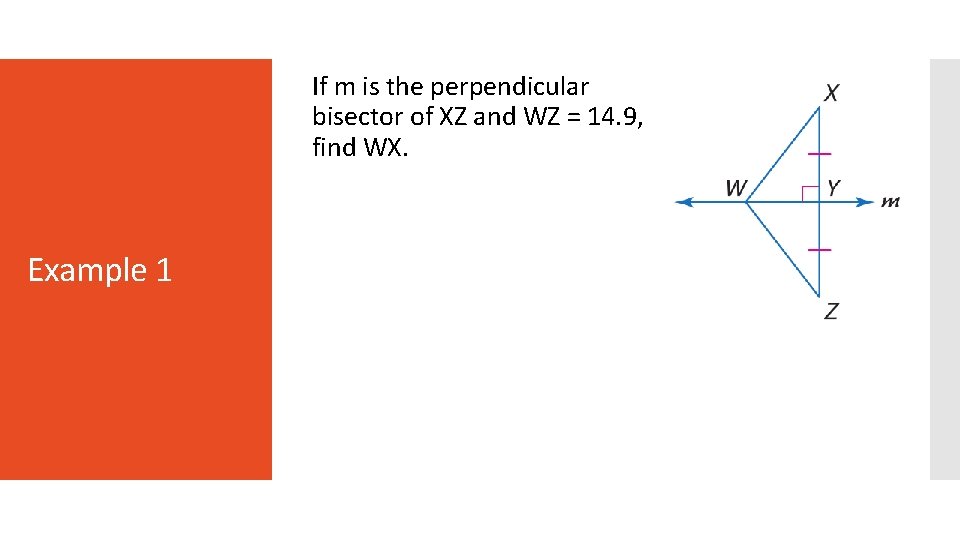
If m is the perpendicular bisector of XZ and WZ = 14. 9, find WX. Example 1

If WX = 25. 3, YZ = 22. 4, and WZ = 25. 3, find XY. Example 1 If m is the perpendicular bisector of XZ, WX = 4 a – 15, and WZ = a + 12, find WX.

Concurrent Lines: Three or more lines that intersect at a common point. Vocabulary Point of Concurrency: The point where concurrent lines intersect.
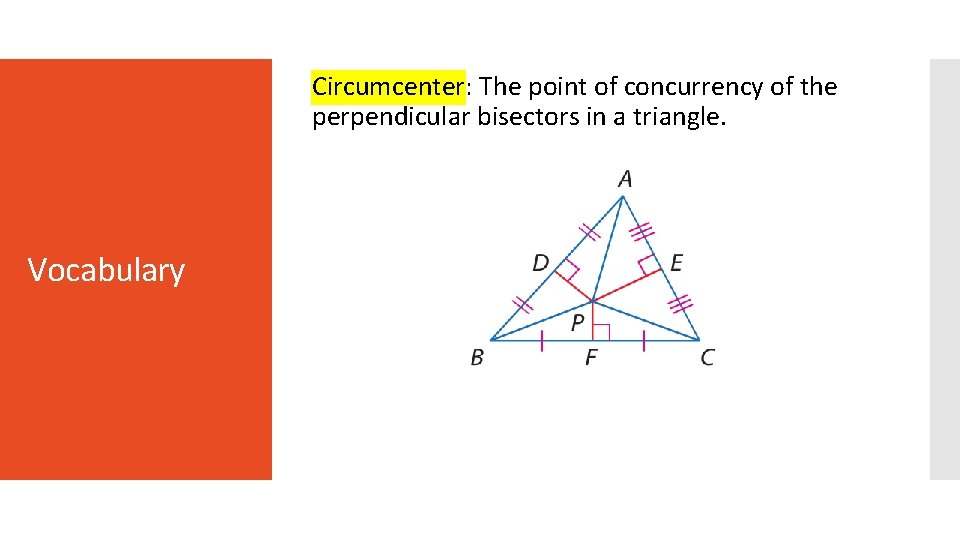
Circumcenter: The point of concurrency of the perpendicular bisectors in a triangle. Vocabulary
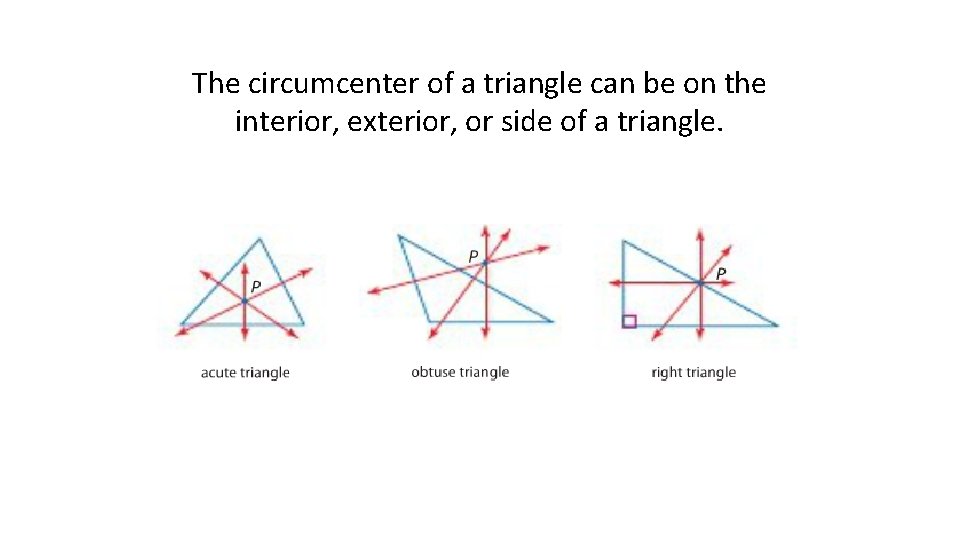
The circumcenter of a triangle can be on the interior, exterior, or side of a triangle.

Circumcenter Theorem
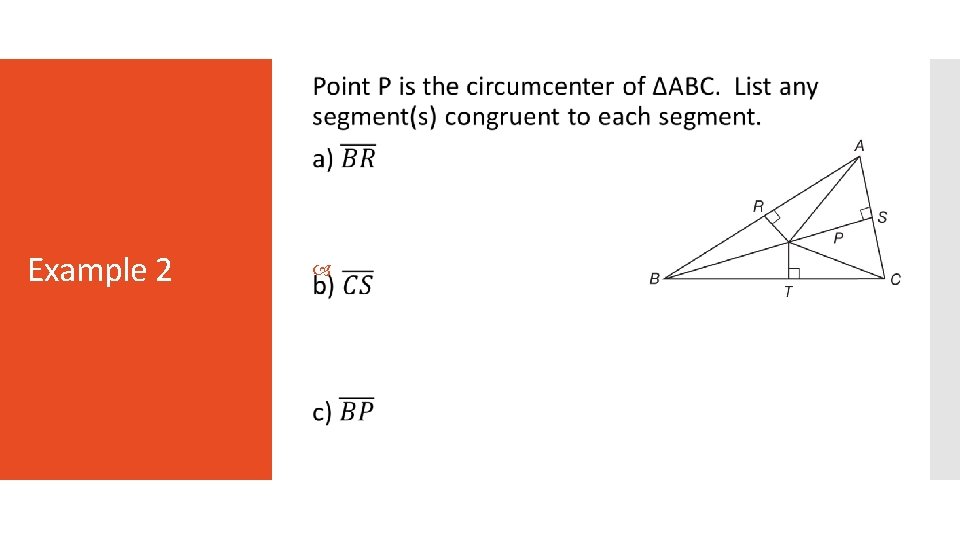
Example 2

Example 2

An angle bisector divides an angle into two congruent angles. Remember!

Angle Bisectors

If m∠BAC = 40, m∠DAC = 40, and DC = 10, find BC. Example 3
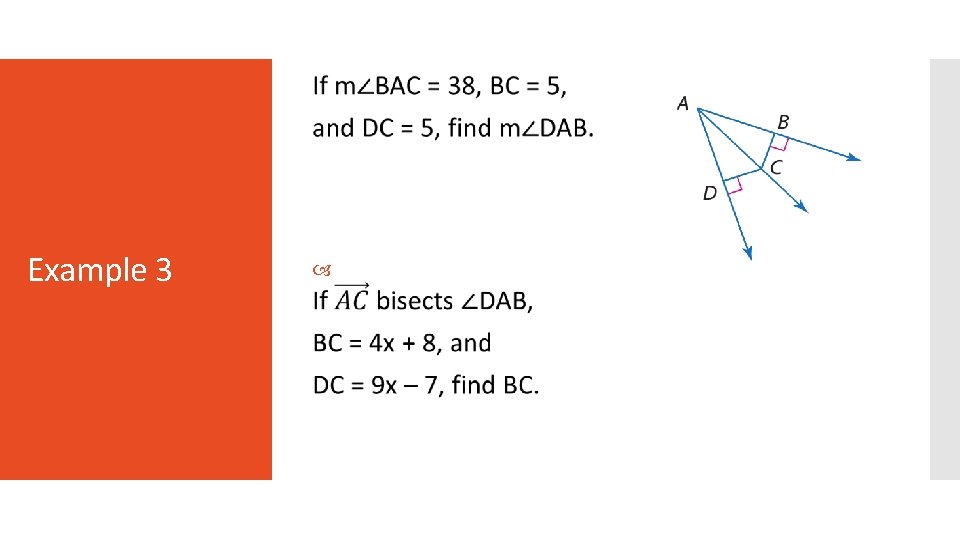
Example 3
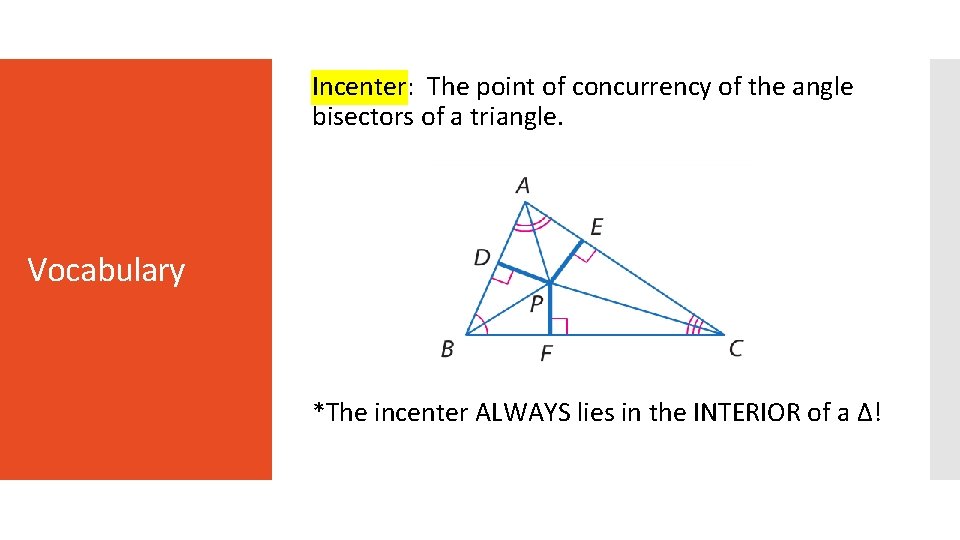
Incenter: The point of concurrency of the angle bisectors of a triangle. Vocabulary *The incenter ALWAYS lies in the INTERIOR of a ∆!

Incenter Theorem
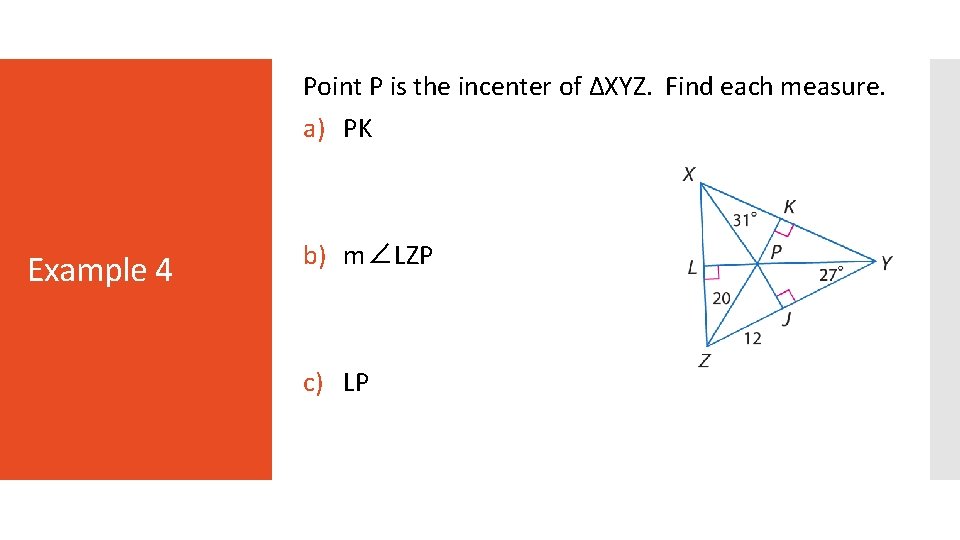
Point P is the incenter of ∆XYZ. Find each measure. a) PK Example 4 b) m∠LZP c) LP
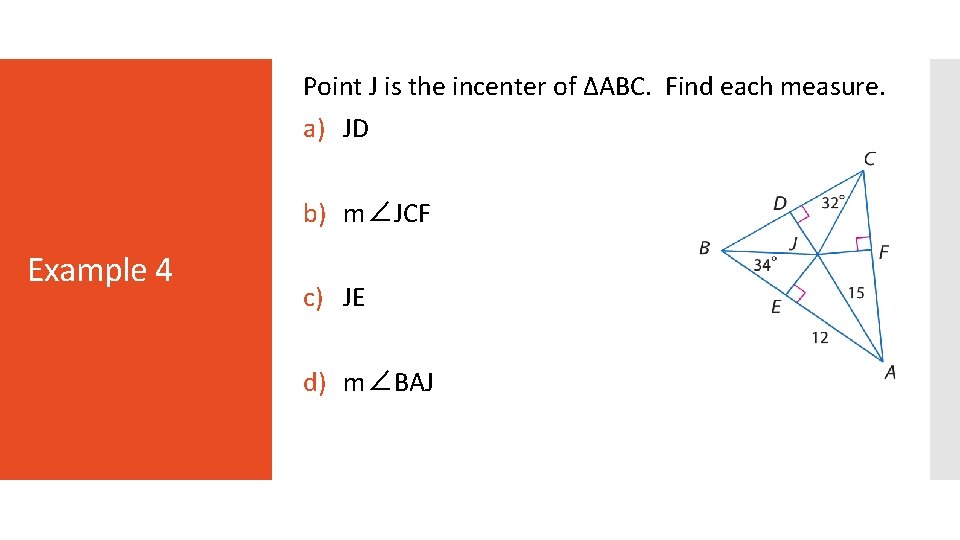
Point J is the incenter of ∆ABC. Find each measure. a) JD b) m∠JCF Example 4 c) JE d) m∠BAJ

Homework p. 329 #1 – 29 odd, skip #15
- Slides: 22