Section 4 5 Linearization and differentials OBJECTIVES STUDENTS

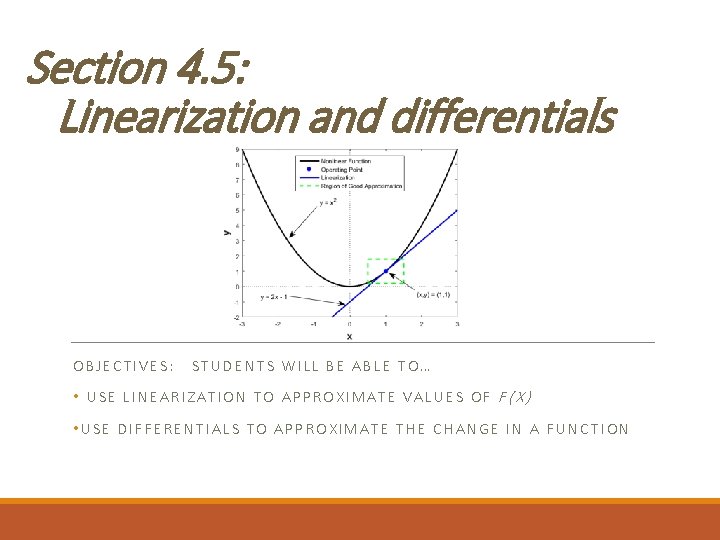
Section 4. 5: Linearization and differentials OBJECTIVES: STUDENTS WILL BE ABLE TO… • USE LINEARIZATION TO APPROXIMATE VALUES OF F(X) • USE DIFFERENTIALS TO APPROXIMATE THE CHANGE IN A FUNCTION

Linear Approximation 1) Graph f(x) = x 2 2) In the same window, graph the tangent line to f at (1, 1) 3) Zoom in three times at the point (1, 1) 4) Use the trace feature to compare the two graphs 5) As the x values get closer to 1, what can you say about y?

Linearization If f is differentiable at x = a, then the approximating function L(x) = f(a) + f’(a)(x – a) is the linearization of f at a. **L(x) is called standard linear approximation x = a is called the center of approximation **Linearization is an application of the tangent line, where the tangent line is used to approximate of the function’s value at x=a.

Examples **NOTE: You need to stay close to point of tangency for it to be a good approximation. Compare the values of the linearization and the value of f(x) as you move away from point of tangency.

Find the linearization of f(x) = 1 + sinx at the point (0, 1)

If you’re given a function of the form (1 + x)k, then its linearization is (1 + kx) where k is any number. Examples: Find the linearization.

Differentials ØApplication of the tangent line ØUses the slope of the tangent line to estimate change in a function’s value when change in x is small. ØGiven a function f(x) we call dy and dx differentials and the relationship between them is given by dy = f‘(x)dx

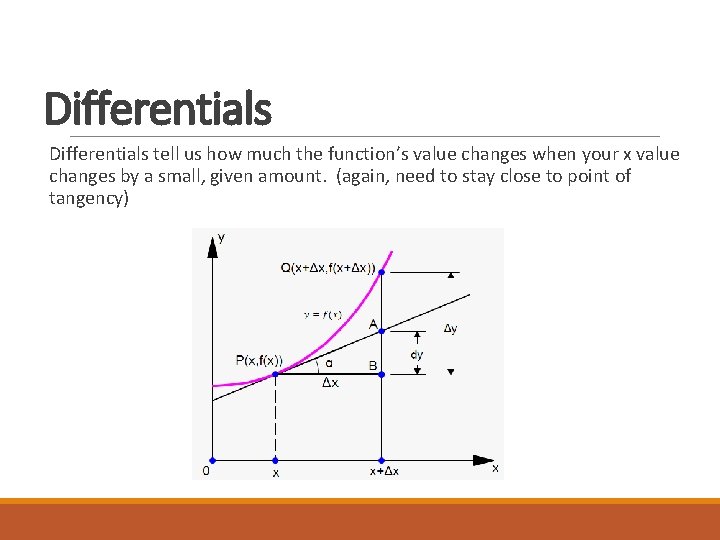
Differentials tell us how much the function’s value changes when your x value changes by a small, given amount. (again, need to stay close to point of tangency)

Examples: Find the differentials for each of the following 1) y = t 3 – 4 t 2 + 7 t 2) w = x 2 sin(2 x) 3) f(z) =

Example Use differentials to determine how much the function y=cos(x 2 +1)- x changes when x changes from 2 to 2. 03?

Differentials can be used to estimate a function’s value:

Applications The radius of a circle in increased from 3. 00 to 3. 03 m. a. ) Estimate the resulting change in area. b. ) Estimate as a percentage of the circle’s original area.

The measurement of the side of a square is found to be 12 inches with a possible error of 1/64 inch. Use differentials to approximate the possible propagated error in computing the area of the square, and the relative error. Propagated error: calculate differential (how would the error of 1/64 inch change the area? ) Relative error =

Tolerance: Estimate the maximum allowable percent error in measuring the side if the error in computing the area cannot exceed 2. 5%. (In other words, how much can the side length be mis-measured to have a computing error < 2. 5%? )

Tolerance: About how accurately should we measure the radius of a sphere to calculate the volume to within 2% of its true value?