Section 4 4 Using Matrix Row Operations Objectives

Section 4. 4 Using Matrix Row Operations

Objectives • Represent a system of linear equations with an augmented matrix. • Solve a system of linear equations using the row reduction method and back substitution.

Introduction: Some systems of linear equations can be solved in a few steps using substitution. However, in the real world, most systems are very large and very complicated. You can use matrix row operations to solve systems of linear equations that would be difficult or impossible to solve by substitution.

Back Substitution This involves solving for one variable first and working backwards to solve for the other variables.

• Example 1:

• Augmented Matrix

Coefficient matrix

Augmented Matrix: Contains the coefficient matrix and the constant matrix. The constants are separated with a line. Augmented matrix Main Diagonal: The elements 3, 1, and -7. We want to get a triangle of zeros below the main diagonal. When they are zero, we can solve by back substitution.

Example 2: Solve the augmented matrix. Augmented matrix Main Diagonal: The elements 1, 4, and 3. There is a triangle of zeros below the main diagonal. We CAN solve by back substitution.

Example 3: Write the augmented matrix for the system of equations. Identify the elements in the main diagonal. Augmented matrix Main Diagonal: The elements 3, -1, and -5.

Homework: Pg 195 – 196 Ex: 1 – 4, 13 – 18

Operations that can be performed without altering the solution set of a linear system 1. Interchange any two rows 2. Multiply every element in a row by a nonzero constant 3. Add a constant multiple of the elements of one row to corresponding elements of another row We are going to work with our augmented matrix to get it in a form that will tell us the solutions to the system of equations. We can only use the above operations or a combination of them to get it in this form.

We use elementary row operations to make the matrix look like the one below. The # signs just mean there can be any number here---we don’t care what. After we get the matrix to look like our goal, we put the variables back in and use back substitution to get the solutions.

Definition: • Performing elementary row operations on a matrix to solve a system of equations is called the row reduction method.

Example 4: Examples of Row Operations Row operation 1 Row operation 2

Example 4: Examples of Row Operations (continued) Row operation 3

Example 5: Solve the system of equations Use row operations to obtain echelon form: We already have the 1 where we need it. The augmented matrix We’ll take row 1 and multiply it by 3 and add to row 2 to get a 0. The notation for this step is 3 R 1 + R 2 Work on this column first. Get the 1 and then use it as a “tool” to get zeros below it with row operations.

3 R 1 + R 2 2 R 1 + R 3 Now our first column is like our goal. 3 R 1 3 6 3 3 + R 2 3 5 1 3 0 1 2 0 2 R 1 + R 3 2 4 2 2 2 0 6 2 7 1 5 1 Now we’ll use 2 times row 1 added to row 3 to get a 0 there.

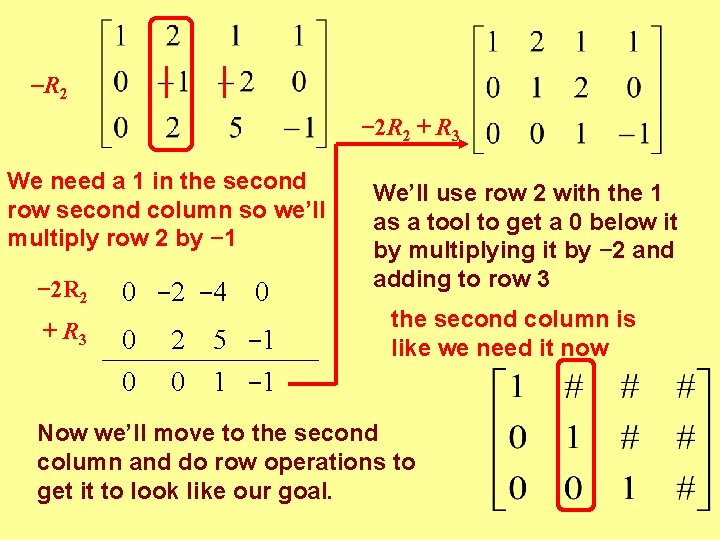
R 2 − 2 R 2 + R 3 We need a 1 in the second row second column so we’ll multiply row 2 by − 1 − 2 R 2 0 − 2 − 4 + R 3 0 0 2 0 0 5 − 1 1 − 1 We’ll use row 2 with the 1 as a tool to get a 0 below it by multiplying it by − 2 and adding to row 3 the second column is like we need it now Now we’ll move to the second column and do row operations to get it to look like our goal.

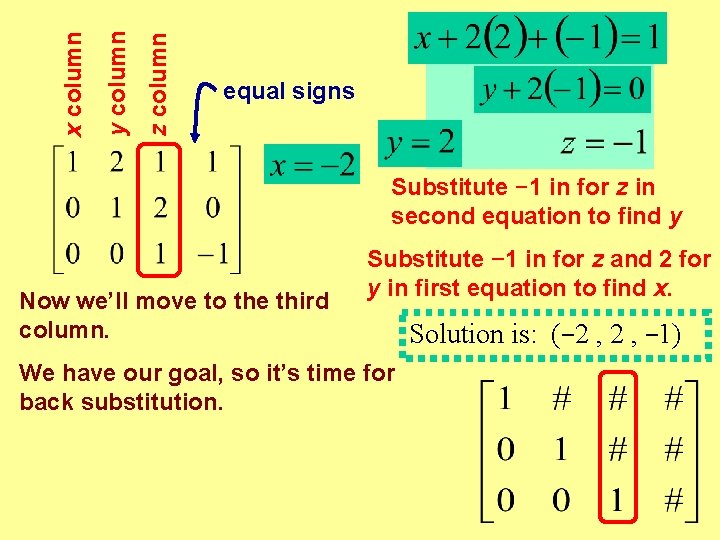
z column y column x column equal signs Substitute − 1 in for z in second equation to find y Now we’ll move to the third column. Substitute − 1 in for z and 2 for y in first equation to find x. We have our goal, so it’s time for back substitution. Solution is: (− 2 , − 1)

Solution is: (− 2 , − 1) Check answer. These are all true. Geometrically this means we have three planes that intersect at a point, a unique solution.

Example 6: Use row operations to solve the system. Solution: Interchange rows 1 and 2. Write the augmented matrix of the system.

Example 6 (cont’d)

Example 6 (cont’d)

Example 6 (cont’d) This matrix gives the system Substitute 1 for z in the second equation.

Example 6 (cont’d) Substitute 2 for y and 1 for z in the first equation. The solution is (2, – 2, 1).

Homework: 4. 4 Practice and Apply

Example 7: Use row operations to solve the system. Solution: Write the augmented matrix.

Example 7: Use row operations to solve the system. The matrix gives the system The false statement indicates that the system is inconsistent and has no solution. The solution set is .

Example 8: Use row operations to solve the system. Solution: Write the augmented matrix.

Example 8: Use row operations to solve the system. The matrix gives the system The true statement indicates that the system has an infinite amount of solutions. The solution set is {(x, y)| x – y = 2}.

Video on Using Calculator to Solve a System of Equations using Matrices • http: //www. youtube. com/watch? v=7 e 1 uyw Dt. Onc • (Start at 7: 35)

Homework: Section 4. 4 Graphing Calculator Exercises

Homework: Pg 196 Ex: 26 -31 (You can check your answers on the graphing calculators) 4. 4 Quiz Tomorrow