Section 4 4 The Derivative in Graphing and

Section 4. 4 The Derivative in Graphing and Applications- “Absolute Maxima and Minima”

All graphics are attributed to: • Calculus, 10/E by Howard Anton, Irl Bivens, and Stephen Davis Copyright © 2009 by John Wiley & Sons, Inc. All rights reserved.

Introduction • In this section we will find the highest and lowest points over the entire “mountain range” instead of the high and low points in their immediate vicinity. • In mathematical terms, we will be looking for the largest and smallest values of a function over an interval.

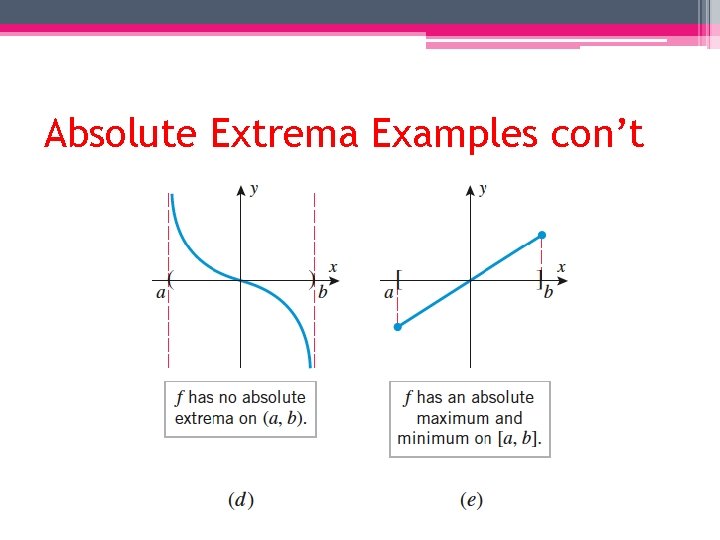
Absolute Extrema • If a function has an absolute maximum at a given point in an interval, then the y-value associated with that point is the largest value of the function on the interval. • Likewise for the absolute minimum and the smallest y-value of the function on the interval. • There is no guarantee that a function will have an absolute max. or min. on a given interval. • See examples on two following slides.

Absolute Extrema Examples

Absolute Extrema Examples con’t

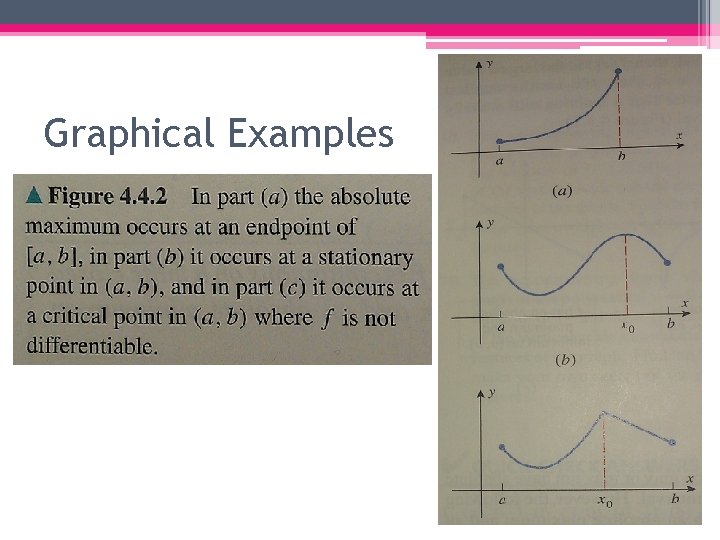
The Extreme Value Theorem • The extreme value theorem tells us under which conditions absolute extrema exist. • We will discuss how to find them on later slides. • In other words, if the function is continuous on [a, b], then the absolute extrema occur either at the endpoints of the interval or at the critical points inside (a, b).

Graphical Examples

Open Interval Application • This is also valid on infinite open intervals such as.

How to Find the Absolute Extrema • This is very similar to finding the relative extrema. • After finding all of the critical points (derivative = 0, solve for x and non-differentiable points), find out which of them is the smallest and largest by substitution into f(x).

Polynomial Example Zero Product Property smallest largest

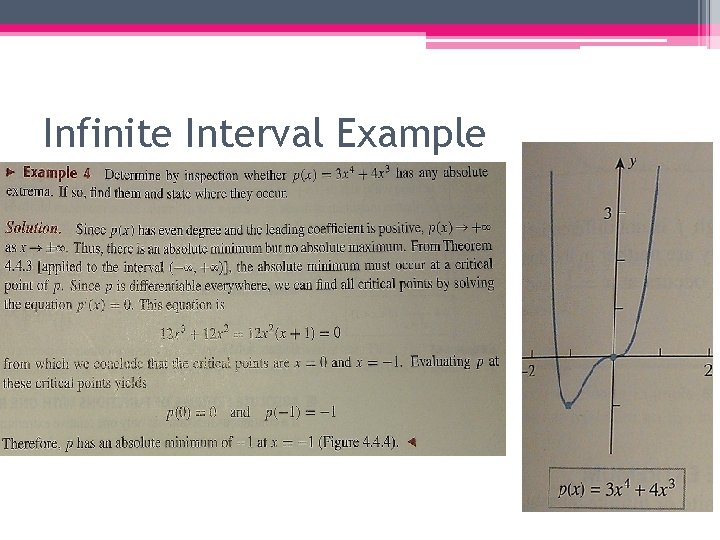
Absolute Extrema on Infinite Intervals •

Infinite Interval Example

Absolute Extrema on Open Intervals • A continuous function may or may not have absolute extrema on an open interval. • There are certain conditions that will help determine whether or not they exist.

Examples • See examples on pages 270 -271

Tea at the Beverly Hills Hotel