Section 4 4 Periodic Functions Stretching and Translating

Section 4 -4 Periodic Functions, Stretching, and Translating Functions Objectives: 1. To determine periodicity and amplitude from graphs 2. To stretch and shrink graphs both vertically and horizontally, and to translate graphs.

Periodic Functions • What does it mean to be periodic? – 1. Having or marked by repeated cycles. – 2. Happening or appearing at regular intervals. – 3. Recurring or reappearing from time to time; intermittent. • What types of things are periodic? – Tides (they rise and fall daily) – Amount of daylight per day (increases and decreases within a period of a year) – The amount of the moon that is visible (moon phases).

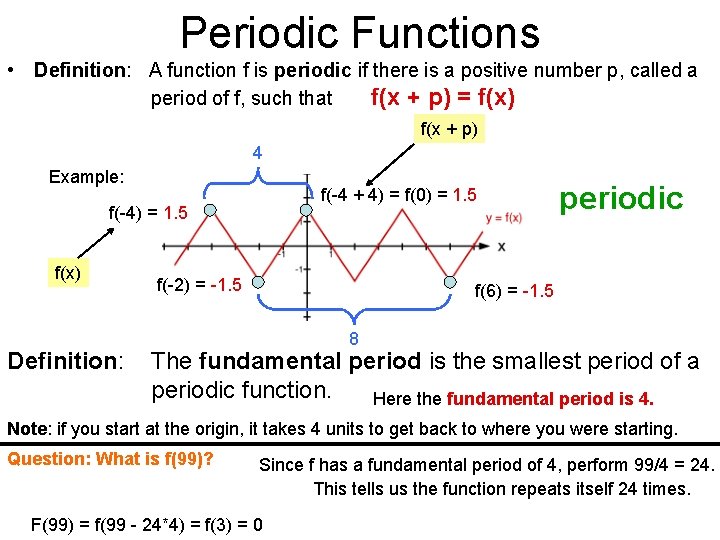
Periodic Functions • Definition: A function f is periodic if there is a positive number p, called a period of f, such that f(x + p) = f(x) f(x + p) 4 Example: f(-4 + 4) = f(0) = 1. 5 f(-4) = 1. 5 f(x) Definition: f(-2) = -1. 5 periodic f(6) = -1. 5 8 The fundamental period is the smallest period of a periodic function. Here the fundamental period is 4. Note: if you start at the origin, it takes 4 units to get back to where you were starting. Question: What is f(99)? Since f has a fundamental period of 4, perform 99/4 = 24. This tells us the function repeats itself 24 times. F(99) = f(99 - 24*4) = f(3) = 0

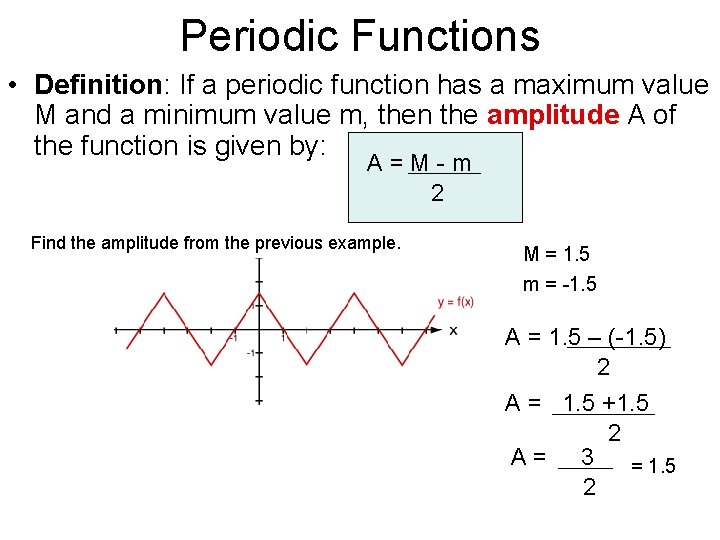
Periodic Functions • Definition: If a periodic function has a maximum value M and a minimum value m, then the amplitude A of the function is given by: A=M-m 2 Find the amplitude from the previous example. M = 1. 5 m = -1. 5 A = 1. 5 – (-1. 5) 2 A = 1. 5 +1. 5 2 A= 3 = 1. 5 2

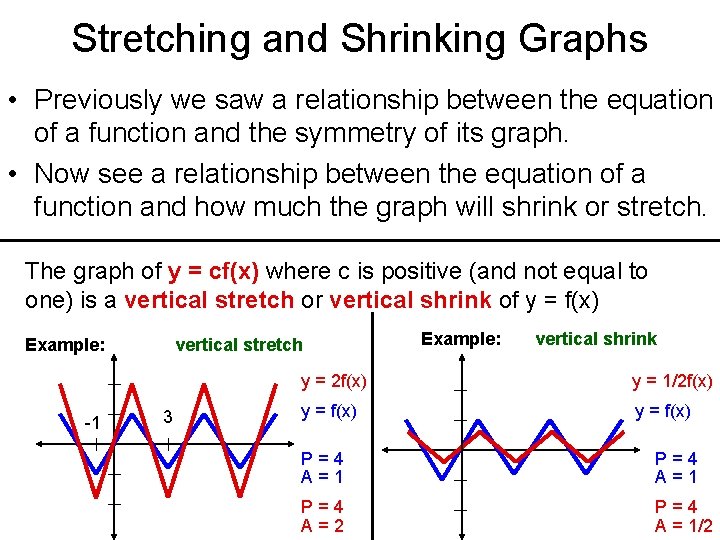
Stretching and Shrinking Graphs • Previously we saw a relationship between the equation of a function and the symmetry of its graph. • Now see a relationship between the equation of a function and how much the graph will shrink or stretch. The graph of y = cf(x) where c is positive (and not equal to one) is a vertical stretch or vertical shrink of y = f(x) Example: -1 vertical stretch 3 Example: vertical shrink y = 2 f(x) y = 1/2 f(x) y = f(x) P=4 A=1 P=4 A=2 P=4 A = 1/2

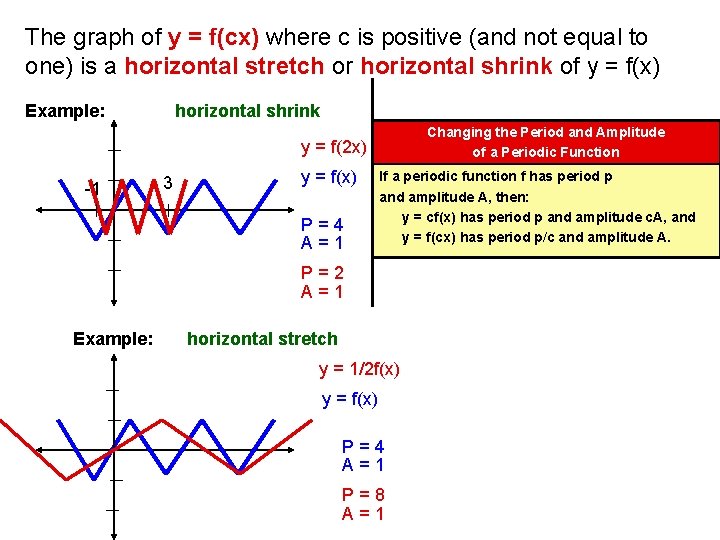
The graph of y = f(cx) where c is positive (and not equal to one) is a horizontal stretch or horizontal shrink of y = f(x) Example: horizontal shrink Changing the Period and Amplitude of a Periodic Function y = f(2 x) -1 3 y = f(x) P=4 A=1 If a periodic function f has period p and amplitude A, then: y = cf(x) has period p and amplitude c. A, and y = f(cx) has period p/c and amplitude A. P=2 A=1 Example: horizontal stretch y = 1/2 f(x) y = f(x) P=4 A=1 P=8 A=1

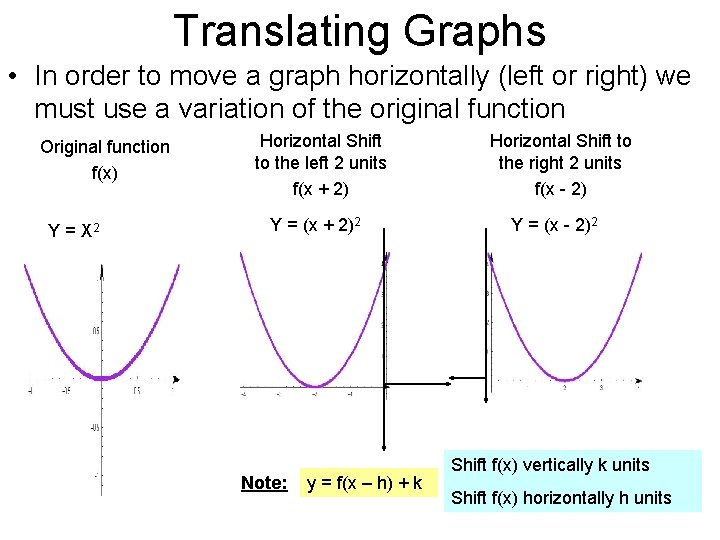
Translating Graphs • In order to move a graph horizontally (left or right) we must use a variation of the original function Original function f(x) Y = X 2 Horizontal Shift to the left 2 units f(x + 2) Y = (x + 2)2 Note: y = f(x – h) + k Horizontal Shift to the right 2 units f(x - 2) Y = (x - 2)2 Shift f(x) vertically k units Shift f(x) horizontally h units

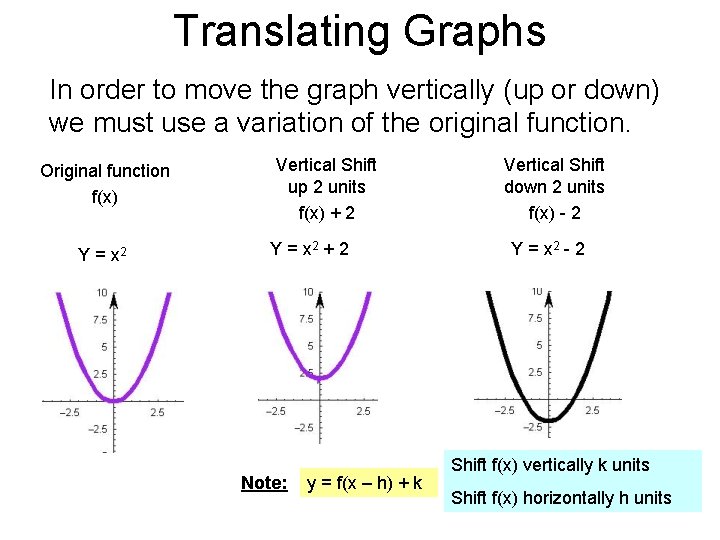
Translating Graphs In order to move the graph vertically (up or down) we must use a variation of the original function. Original function f(x) Y = x 2 Vertical Shift up 2 units f(x) + 2 Y = x 2 + 2 Note: y = f(x – h) + k Vertical Shift down 2 units f(x) - 2 Y = x 2 - 2 Shift f(x) vertically k units Shift f(x) horizontally h units

Translating Graphs If the equation y = f(x) is changed to: Then the graph of y = f(x) is: Reflected in the x-axis Unchanged when f(x) ≥ 0 and reflected in the y-axis Reflected in the line y = x Stretched vertically Shrunk horizontally Stretched horizontally Translated h units horizontally and k units vertically

Section 4 -5 Inverse Functions Objective: To find the inverse of a function, if the inverse exists.

Homework • p 143 -144: 1 -4 (all), 5 -15 (odd)