Section 4 4 Heat Capacity Specific Heat The































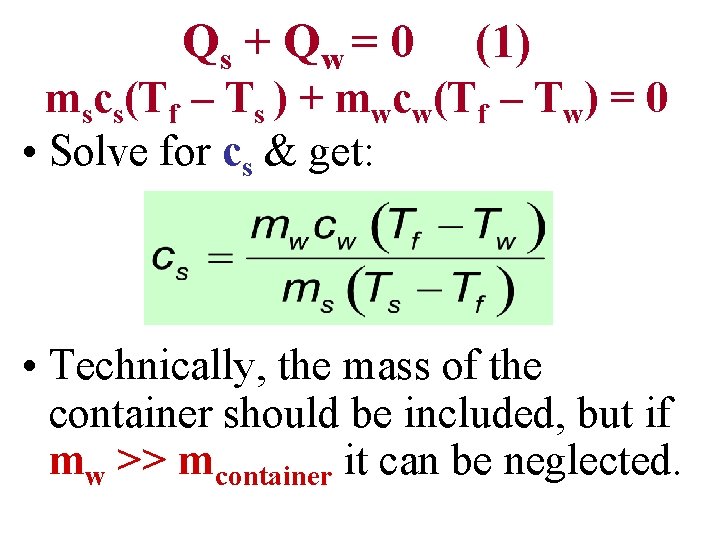



- Slides: 39

Section 4. 4: Heat Capacity & Specific Heat

• The Heat Capacity of a substance is defined as: Cy(T) (đQ/d. T)y • Subscript y says that property y of the substance is held constant when Cy is measured.

• The Heat Capacity of a substance is defined as: Cy(T) (đQ/d. T)y • Subscript y says that property y of the substance is held constant when Cy is measured. • When using this definition, recall that (đQ/d. T)y is NOT a derivative because đQ isn’t an Exact Differential! • Instead, (đQ/d. T)y is a ratio of the 2 infinitesimal quantities đQ & d. T evaluated at constant y.

• Heat Capacity: Cy(T) (đQ/d. T)y • Specific Heat per Kilogram of mass m: mcy(T) (đQ/d. T)y • Specific Heat per Mole of υ moles: υcy(T) (đQ/d. T)y

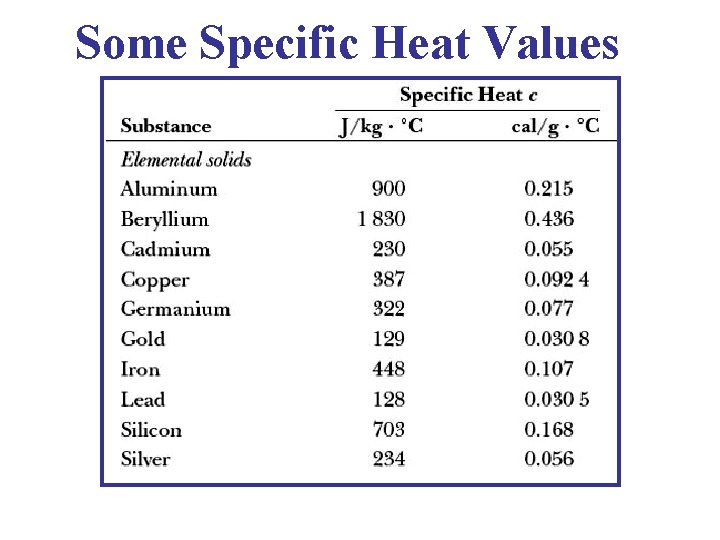
Heat Capacity • The Heat Capacity is Substance C Copper 0. 384 different for each substance. Wax 0. 80 • It also depends on temperature, Aluminum 0. 901 volume & other, parameters. Wood Water 2. 01 4. 18 • If substance A has a higher heat capacity than substance B, it means that More Heat is Needed to cause A to have a certain temperature rise ΔT than is needed to cause B to have the same rise in temperature.

Some Specific Heat Values

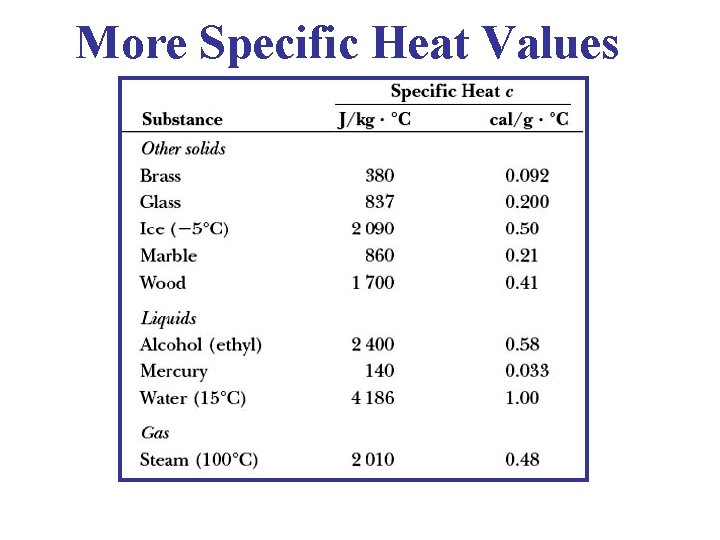
More Specific Heat Values

More Specific Heat Values

Infinitesimal, Quasistatic Processes • 1 st Law of Thermodynamics: đQ = dĒ + đW (1)

Infinitesimal, Quasistatic Processes • 1 st Law of Thermodynamics: đQ = dĒ + đW (1) nd • 2 Law of Thermodynamics: đQ = Td. S (heat reservoir) (2) d. S = Entropy Change

Infinitesimal, Quasistatic Processes • 1 st Law of Thermodynamics: đQ = dĒ + đW (1) nd • 2 Law of Thermodynamics: đQ = Td. S (heat reservoir) (2) d. S = Entropy Change • S is a state function, so d. S is an exact differential. Combining (1) & (2) gives: Td. S = dĒ + đW

• The combined 1 st & 2 nd Laws for infinitesimal quasistatic processes: đQ = Td. S = dĒ + đW (3) (We’ll use this form repeatedly in Ch. 5!)

• The combined 1 st & 2 nd Laws for infinitesimal quasistatic processes: đQ = Td. S = dĒ + đW (3) (We’ll use this form repeatedly in Ch. 5!) • Use this result with the definition of Heat Capacity at constant parameter y: Cy(T) (đQ/d. T)y (4)

• The combined 1 st & 2 nd Laws for infinitesimal quasistatic processes: đQ = Td. S = dĒ + đW (3) (We’ll use this form repeatedly in Ch. 5!) • Use this result with the definition of Heat Capacity at constant parameter y: Cy(T) (đQ/d. T)y (4) • For parameter y, entropy S = S(T, y). So formally, we can write the exact differential of S as d. S = [( S/ T) ]d. T + [( S/ y) ]dy (5)

• Combining (3) and (5) we can write: đQ = Td. S = T[( S/ T)y]d. T + T[( S/ y)T]dy

• Combining (3) and (5) we can write: đQ = Td. S = T[( S/ T)y]d. T + T[( S/ y)T]dy • Use this result with the definition of Heat Capacity at constant parameter y: Cy(T) (đQ/d. T)y

• Combining (3) and (5) we can write: đQ = Td. S = T[( S/ T)y]d. T + T[( S/ y)T]dy • Use this result with the definition of Heat Capacity at constant parameter y: Cy(T) (đQ/d. T)y • This gives the GENERAL RESULT: Cy(T) T( S/ T)y

1 st Law of Thermo: đQ = dĒ + đW (a) • If the volume V is the only external parameter, đW = pd. V.

1 st Law of Thermo: đQ = dĒ + đW (a) • If the volume V is the only external parameter, đW = pd. V. • In constant volume conditions (d. V = 0) & đQ = dĒ • So, the Heat Capacity at Constant Volume is: CV(T) (đQ/d. T)V = ( Ē/ T)V

1 st Law of Thermo: đQ = dĒ + đW (a) • If the volume V is the only external parameter, đW = pd. V. • In constant volume conditions (d. V = 0) & đQ = dĒ • So, the Heat Capacity at Constant Volume is: CV(T) (đQ/d. T)V = ( Ē/ T)V • However, if the Pressure p is held constant, the 1 st Law must be used in the form đQ = dĒ + đW • So, the Heat Capacity at Constant Pressure has the form: Cp(T) (đQ/d. T)p

• 1 st Law of Thermo: đQ = dĒ + đW = dĒ + pd. V

• 1 st Law of Thermo: đQ = dĒ + đW = dĒ + pd. V • Heat Capacity (Constant Volume): CV(T) (đQ/d. T)V = ( Ē/ T)V

• 1 st Law of Thermo: đQ = dĒ + đW = dĒ + pd. V • Heat Capacity (Constant Volume): CV(T) (đQ/d. T)V = ( Ē/ T)V • Heat Capacity (Constant Pressure): Cp(T) (đQ/d. T)p

• Clearly, in general, Cp ≠ CV. • Further, in general, Cp > CV. • However, the measured Cp & CV are very similar for solids & liquids, but very different for gases, so be sure you know which one you’re using if you look one up in a table!

Heat Capacity Measurements for Constant Volume Processes (cv) T Insulation m Heat Q added Insulation m • Heat is added to a substance of mass m in a fixed volume enclosure, which causes a change in internal energy, Ē. The 1 st Law is (if no work is done!): Q = Ē 2 - Ē 1 = Ē = mcv T

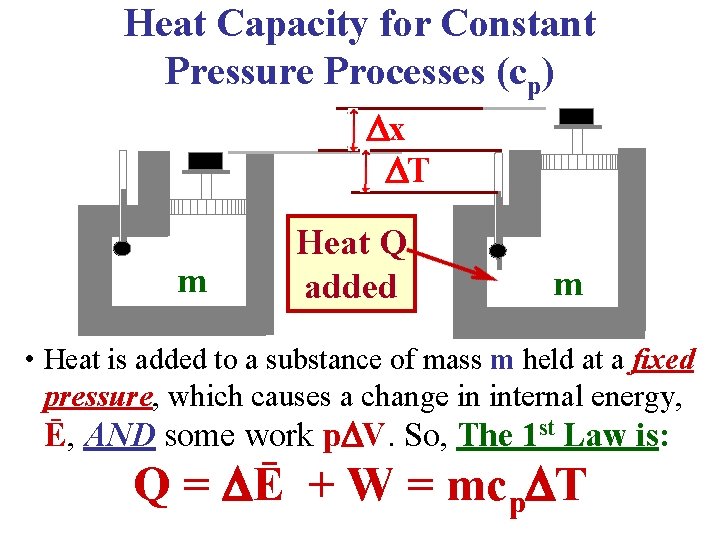
Heat Capacity for Constant Pressure Processes (cp) x T m Heat Q added m • Heat is added to a substance of mass m held at a fixed pressure, which causes a change in internal energy, Ē, AND some work p V. So, The 1 st Law is: Q = Ē + W = mcp T

Experimental Heat Capacity • Experimentally, it is generally easier to add heat at constant pressure than at constant volume. • So, tables typically report Cp for various materials.

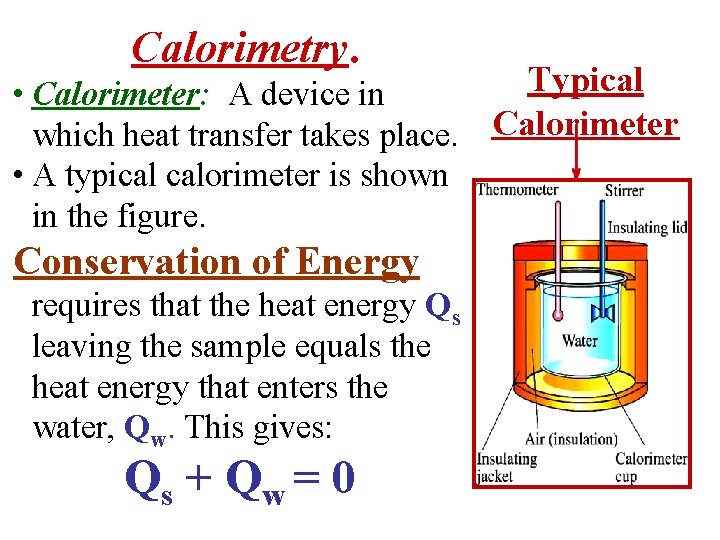
Calorimetry Example: Similar to Reif, pages 141 -142 • A technique to Measure Specific Heat is to heat a sample of material, add it to water, & record the final temperature. • This technique is called Calorimetry. Calorimeter A device in which heat transfer takes place.

Calorimetry. Typical • Calorimeter: A device in which heat transfer takes place. Calorimeter • A typical calorimeter is shown in the figure. Conservation of Energy requires that the heat energy Qs leaving the sample equals the heat energy that enters the water, Qw. This gives: Qs + Q w = 0

Qs + Q w = 0 (1) • Sample Properties: Mass = ms. Initial Temperature = Ts. Specific Heat = cs (unknown)

Qs + Q w = 0 (1) • Sample Properties: Mass = ms. Initial Temperature = Ts. Specific Heat = cs (unknown) • Water Properties: Mass = mw. Initial Temperature = Tw. Specific Heat = cw (4, 286 J/(kg K))

Qs + Q w = 0 (1) • Sample Properties: Mass = ms. Initial Temperature = Ts. Specific Heat = cs (unknown) • Water Properties: Mass = mw. Initial Temperature = Tw. Specific Heat = cw (4, 286 J/(kg K)) • Final Temperature (sample + water) = Tf

• Put all of this into Equation (1) Qs + Q w = 0 (1)

• Put all of this into Equation (1) Qs + Q w = 0 (1) • Assume c. W & cs are independent of temperature T. Use Qs mscs(Tf – Ts ) Qw mwcw(Tf – Tw)

• Put all of this into Equation (1) Qs + Q w = 0 (1) • Assume c. W & cs are independent of temperature T. Use Qs mscs(Tf – Ts ) Qw mwcw(Tf – Tw) • This gives: mscs(Tf – Ts ) + mwcw(Tf – Tw) = 0
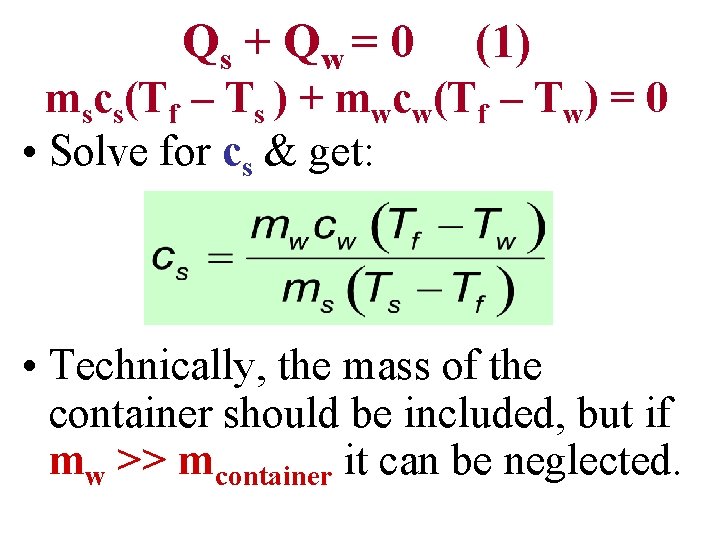
Qs + Q w = 0 (1) mscs(Tf – Ts ) + mwcw(Tf – Tw) = 0 • Solve for cs & get: • Technically, the mass of the container should be included, but if mw >> mcontainer it can be neglected.

• Consider now a slightly different problem. 2 substances A & B, initially at different temperatures TA & TB. • The specific heats c. A & c. B are known. • The final temperature Tf is unknown. All steps are the same as the previous example until near the end! QA + Q B = 0 (1)

QA + Q B = 0 (1) • Sample Properties: Mass A = m. A. Initial Temperature = TA. Specific Heat = c. A Mass B = m. B. Initial Temperature = TB. Specific Heat = c. B • Final Temperature (A + B) = Tf (Unknown)

QA + Q B = 0 (1) • Assume: c. A & c. B are independent of temperature T. • Put QA m. Ac. A(Tf – TA) & QB m. Bc. B(Tf – TB) into (1): m. Ac. A(Tf – TA ) + m. Bc. B(Tf – TB) = 0 • Solve for Tf & get: Tf = (m. Ac. ATA + m. Bc. BTB)∕(m. Ac. A + m. Bc. B)
 Specific heat capacity table pdf
Specific heat capacity table pdf Unit for specific heat capacity
Unit for specific heat capacity When you heat sugar what happens
When you heat sugar what happens Specific heat capacity of ice cream
Specific heat capacity of ice cream Debye model
Debye model Definition of specific latent heat
Definition of specific latent heat Heat calculations
Heat calculations Latent heat capacity
Latent heat capacity How to solve for specific heat
How to solve for specific heat What is enthalpy of fusion
What is enthalpy of fusion How to find the specific heat capacity
How to find the specific heat capacity Symbol of specific heat capacity
Symbol of specific heat capacity Required practical specific heat capacity
Required practical specific heat capacity Latent heat of lead
Latent heat of lead Qlost = qgained
Qlost = qgained Specific heat capacity calculator
Specific heat capacity calculator Heat capacity si unit
Heat capacity si unit Specific heat capacity of lead j/kg c
Specific heat capacity of lead j/kg c Investigating specific heat capacity
Investigating specific heat capacity Enthalpy vs heat capacity
Enthalpy vs heat capacity Specific heat capacity of lead j/kg c
Specific heat capacity of lead j/kg c Specific heat capacity of cheese
Specific heat capacity of cheese Specific heat capacity calculator
Specific heat capacity calculator How to find mass from specific heat
How to find mass from specific heat Si unit of specific heat capacity
Si unit of specific heat capacity Heat and temperature
Heat and temperature Specific heat capacity equation triangle
Specific heat capacity equation triangle Specific heat
Specific heat Heat capacity of rubber
Heat capacity of rubber Specific heat capacity of water
Specific heat capacity of water Specific heat capacity
Specific heat capacity Thermal energy equations
Thermal energy equations Specific heat capacity
Specific heat capacity What is specific heat capacity
What is specific heat capacity Name
Name Cp for monatomic gas
Cp for monatomic gas Per 理想
Per 理想 Specific heat capacity
Specific heat capacity Specific heat capacity of aluminium
Specific heat capacity of aluminium Specific latent heat of a substance
Specific latent heat of a substance