Section 4 3 2 Conditional Distributions and Simpsons

Section 4. 3. 2 Conditional Distributions and Simpson’s Paradox AP Statistics www. toddfadoir. com/apstats AP Statistics, Section 4. 3, Part 2

Calculating Conditional Distributions n The “conditional” part sounds like ¨ “on the condition the respondents are 35 to 54” ¨ “among those who have completed high school but did not go to college” ¨ “for those respondents over 55 years of age” 25 to 34 35 to 54 55+ Total Did not complete HS 4, 474 9, 155 14, 224 27, 853 Completed HS 11, 546 26, 481 20, 060 58, 087 1 to 3 years of college 10, 700 22, 618 11, 127 44, 445 4+ years of college 11, 066 23, 183 10, 596 44, 845 Total 37, 786 81, 435 56, 008 175, 230 AP Statistics, Section 4. 3, Part 2 2

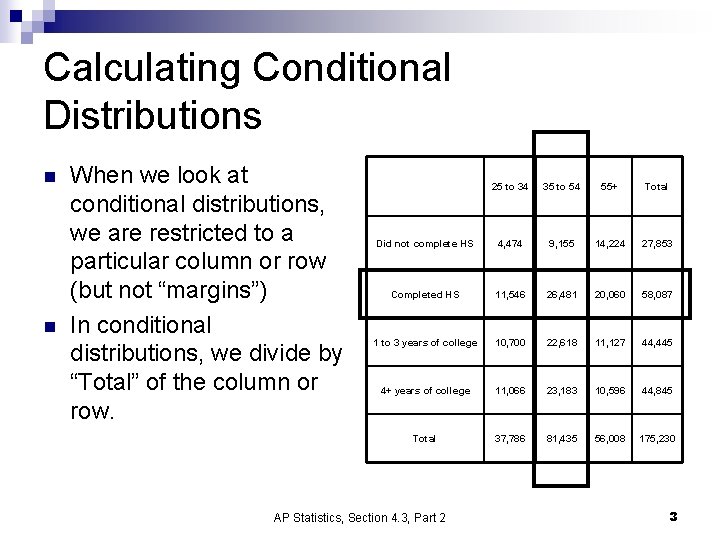
Calculating Conditional Distributions n n When we look at conditional distributions, we are restricted to a particular column or row (but not “margins”) In conditional distributions, we divide by “Total” of the column or row. 25 to 34 35 to 54 55+ Total Did not complete HS 4, 474 9, 155 14, 224 27, 853 Completed HS 11, 546 26, 481 20, 060 58, 087 1 to 3 years of college 10, 700 22, 618 11, 127 44, 445 4+ years of college 11, 066 23, 183 10, 596 44, 845 Total 37, 786 81, 435 56, 008 175, 230 AP Statistics, Section 4. 3, Part 2 3

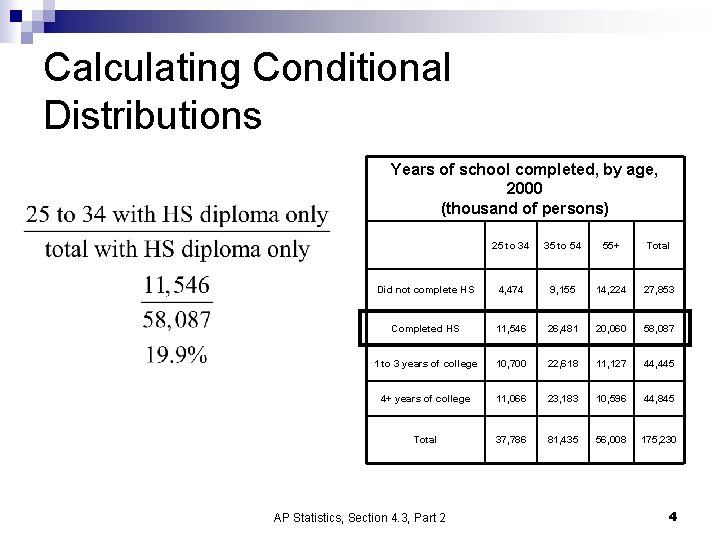
Calculating Conditional Distributions Years of school completed, by age, 2000 (thousand of persons) 25 to 34 35 to 54 55+ Total Did not complete HS 4, 474 9, 155 14, 224 27, 853 Completed HS 11, 546 26, 481 20, 060 58, 087 1 to 3 years of college 10, 700 22, 618 11, 127 44, 445 4+ years of college 11, 066 23, 183 10, 596 44, 845 Total 37, 786 81, 435 56, 008 175, 230 AP Statistics, Section 4. 3, Part 2 4

Calculating Conditional Distributions Years of school completed, by age, 2000 (thousand of persons) 25 to 34 35 to 54 55+ Total Did not complete HS 4, 474 9, 155 14, 224 27, 853 Completed HS 11, 546 26, 481 20, 060 58, 087 1 to 3 years of college 10, 700 22, 618 11, 127 44, 445 4+ years of college 11, 066 23, 183 10, 596 44, 845 Total 37, 786 81, 435 56, 008 175, 230 AP Statistics, Section 4. 3, Part 2 5

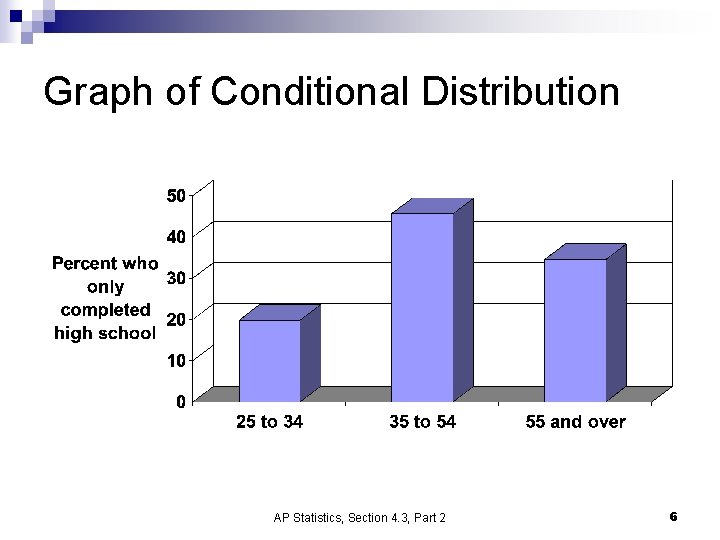
Graph of Conditional Distribution AP Statistics, Section 4. 3, Part 2 6

Simpson’s Paradox A paradox is “a statement that is seemingly contradictory or opposed to common sense and yet is perhaps true” (m -w. com) n Simpson’s Paradox involves percentages… n AP Statistics, Section 4. 3, Part 2 7

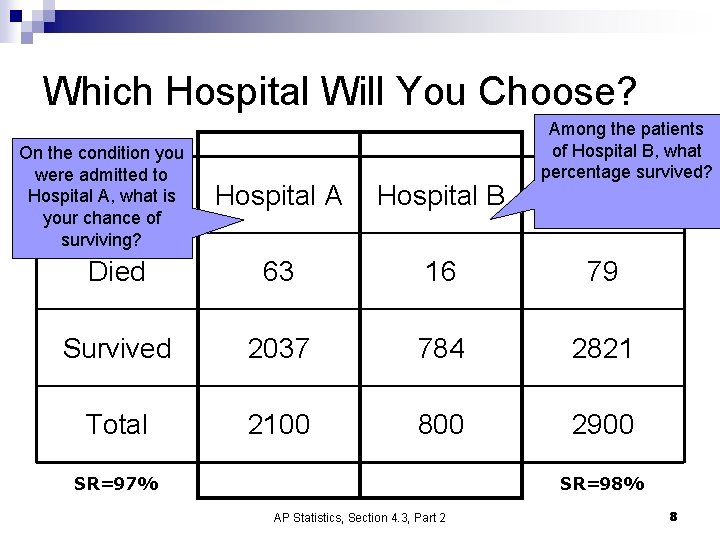
Which Hospital Will You Choose? On the condition you were admitted to Hospital A, what is your chance of surviving? Among the patients of Hospital B, what percentage survived? Hospital A Hospital B Died 63 16 79 Survived 2037 784 2821 Total 2100 800 2900 SR=97% Total SR=98% AP Statistics, Section 4. 3, Part 2 8

What if you are in “good” condition? If you were admitted to Hospital A in good condition, what is your chance of surviving? Amongst Hospital B patients in good condition, what percentage Total lived? Hospital A Hospital B Died 6 8 14 Survived 594 592 1186 Total 600 1200 SR=99. 0% SR=98. 6% AP Statistics, Section 4. 3, Part 2 9

What if you are in “poor” condition? If you were admitted to Hospital A in poor condition, what is your chance of living? Among Hospital B patients in poor condition, what percentage Total lived? Hospital A Hospital B Died 57 8 65 Survived 1443 192 1635 Total 1500 200 1700 SR=96. 2% SR=96. 0% AP Statistics, Section 4. 3, Part 2 10

The choice reverses… when we add the third variable. n This happens very rarely. n AP Statistics, Section 4. 3, Part 2 11

Assignment n Exercises: 4. 59 -4. 61 AP Statistics, Section 4. 3, Part 2 12