Section 4 2 Measuring Evidence with pvalues Statistics

Section 4. 2 Measuring Evidence with p-values Statistics: Unlocking the Power of Data Lock 5

Question of the Day Does drinking tea boost your immune system? Statistics: Unlocking the Power of Data Lock 5

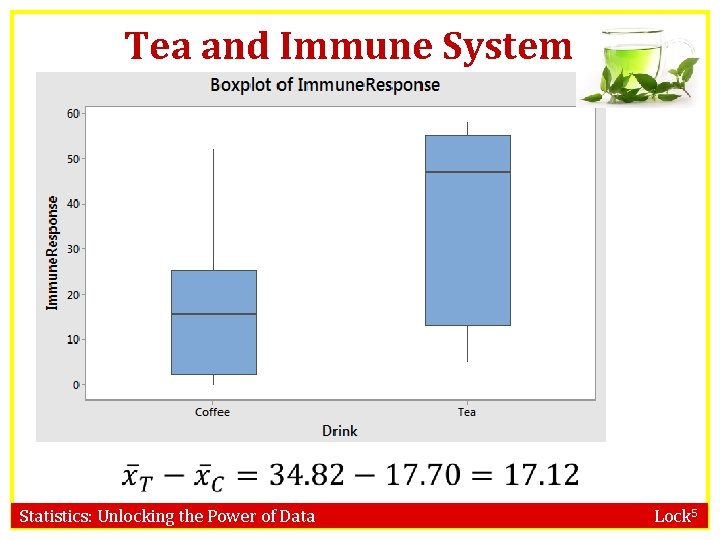
Tea and Immune Response • Participants were randomized to drink five or six cups of either tea (black) or coffee every day for two weeks (both drinks have caffeine but only tea has L-theanine) • After two weeks, blood samples were exposed to an antigen, and production of interferon gamma (immune system response) was measured • Explanatory variable: tea or coffee • Response variable: immune system response • Does drinking tea actually boost your immunity? Antigens in tea-Beverage Prime Human Vγ 2 Vδ 2 T Cells in vitro and in vivo for Memory and Nonmemory Antibacterial Cytokine Responses, Kamath et. al. , Proceedings of the National Academy of Sciences, May 13, 2003. Statistics: Unlocking the Power of Data Lock 5

Tea and the Immune System If the tea drinkers have enough higher levels of immune system response, can we conclude that drinking tea rather than coffee caused an increase in this aspect of the immune response? a) Yes Randomized experiment allows conclusions about causality b) No Statistics: Unlocking the Power of Data Lock 5

Review µT = mean immune system response after drinking tea µC = mean immune system response after drinking coffee Does drinking tea boost immunity? The relevant hypotheses are: a) H 0: µT > µC, Ha: µT = µC b) H 0: µT < µC, Ha: µT = µC c) H 0: µT = µC, Ha: µT > µC d) H 0: µT = µC, Ha: µT < µC e) H 0: µT = µC, Ha: µT ≠ µC Statistics: Unlocking the Power of Data Lock 5

Tea and Immune System The explanatory variable is tea or coffee, and the response variable is immune system response measured in amount of interferon gamma produced. How could we visualize this data? a) Bar chart One categorical and one quantitative b) Histogram c) Side-by-side boxplots d) Scatterplot Statistics: Unlocking the Power of Data Lock 5

Tea and Immune System Statistics: Unlocking the Power of Data Lock 5

Two Plausible Explanations �Why might the tea drinkers have higher levels of immune system response? �Two plausible explanations: Alternative true: Tea drinkers have higher immune system responses than coffee drinkers Null true, random chance: the people who got randomly assigned to the tea group have better immune systems than those who got randomly assigned to the coffee group Statistics: Unlocking the Power of Data Lock 5

The Plausibility of the Null �The goal is determine whether the null hypothesis and random chance are a plausible explanation, given the observed data What kinds of statistics might we get, just by random chance, if the null hypothesis were true? Statistics: Unlocking the Power of Data Lock 5

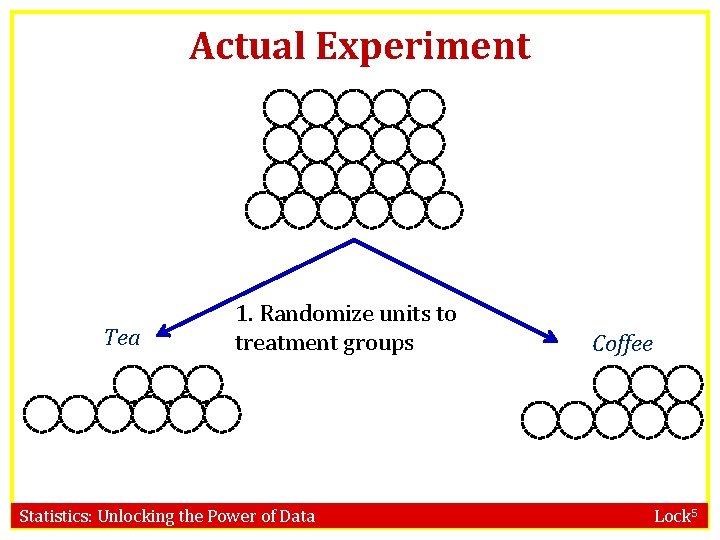
Actual Experiment R R R R R R 1. Randomize units to treatment groups Tea R R Coffee R R R Statistics: Unlocking the Power of Data R R R R Lock 5

Actual Experiment 1. Randomize units to treatment groups 2. Conduct experiment 3. Measure response variable Tea R 5 R 13 R 18 R 20 R 11 R 48 R 52 R 55 R 56 R 58 R 47 Statistics: Unlocking the Power of Data Coffee R 0 R 3 R 15 R 11 R 21 R 38 R 52 R 16 Lock 5

Actual Experiment 1. Randomize units to treatment groups 2. Conduct experiment 3. Measure response variable 4. Calculate statistic Tea R 5 R 13 R 18 R 20 R 11 R 48 R 52 R 55 R 56 R 58 R 47 Statistics: Unlocking the Power of Data Coffee R 0 R 3 R 15 R 11 R 21 R 38 R 52 R 16 Lock 5

Actual Experiment �Two plausible explanations: Tea boosts immunity Random chance What might happen just by random chance? ? ? Tea R 5 R 13 R 18 R 20 R 11 R 48 R 52 R 55 R 56 R 58 R 47 Statistics: Unlocking the Power of Data Coffee R 0 R 3 R 15 R 11 R 21 R 38 R 52 R 16 Lock 5

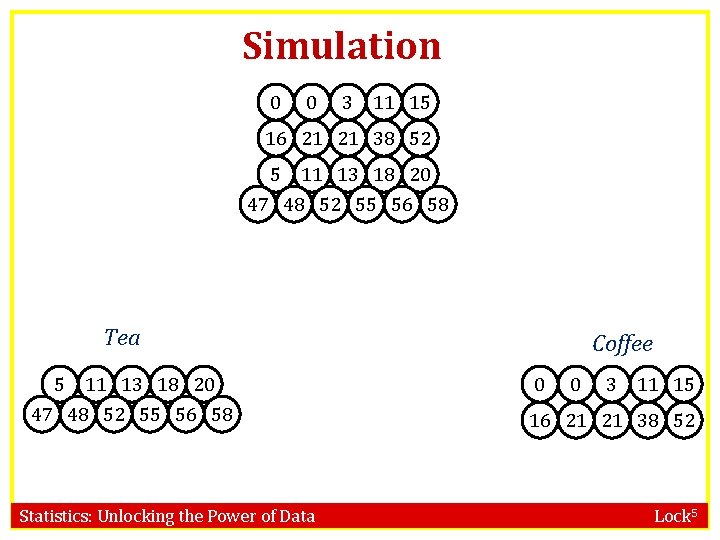
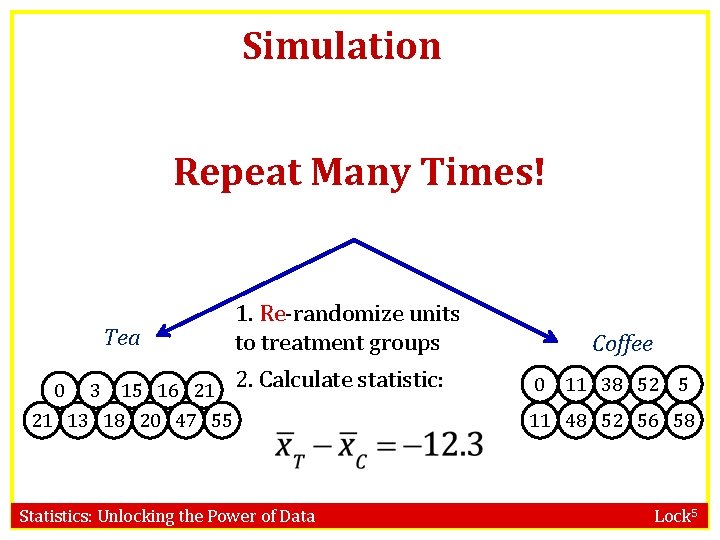
Simulation R 0 R 3 R 15 R 11 R 21 R 38 R 52 R 16 R 5 R 13 R 18 R 20 R 11 R 48 R 52 R 55 R 56 R 58 R 47 Tea R 5 R 13 R 18 R 20 R 11 R 48 R 52 R 55 R 56 R 58 R 47 Statistics: Unlocking the Power of Data Coffee R 0 R 3 R 15 R 11 R 21 R 38 R 52 R 16 Lock 5

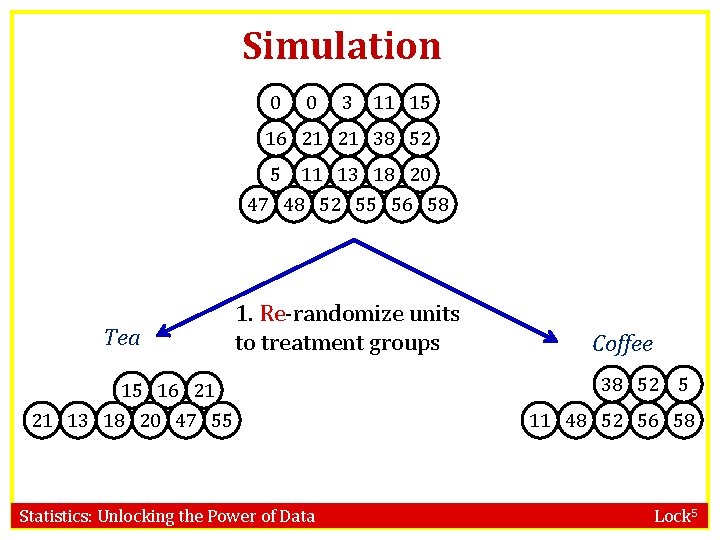
Simulation 0 0 R 3 11 15 R 21 R 38 R 52 R 16 R 5 R 13 R 18 R 20 R 11 R 48 R 52 R 55 R 56 R 58 R 47 Tea 1. Re-randomize units to treatment groups R 16 R 21 R 15 R 13 R 18 R 20 R 47 R 55 R 21 Statistics: Unlocking the Power of Data Coffee R 52 R R 38 5 R 48 R 52 R 56 R 58 R 11 Lock 5

Simulation Repeat Many Times! Tea 0 R 16 R 21 R 3 15 R 13 R 18 R 20 R 47 R 55 R 21 1. Re-randomize units to treatment groups 2. Calculate statistic: Statistics: Unlocking the Power of Data Coffee R 0 R 38 R 52 R R 11 5 R 48 R 52 R 56 R 58 R 11 Lock 5

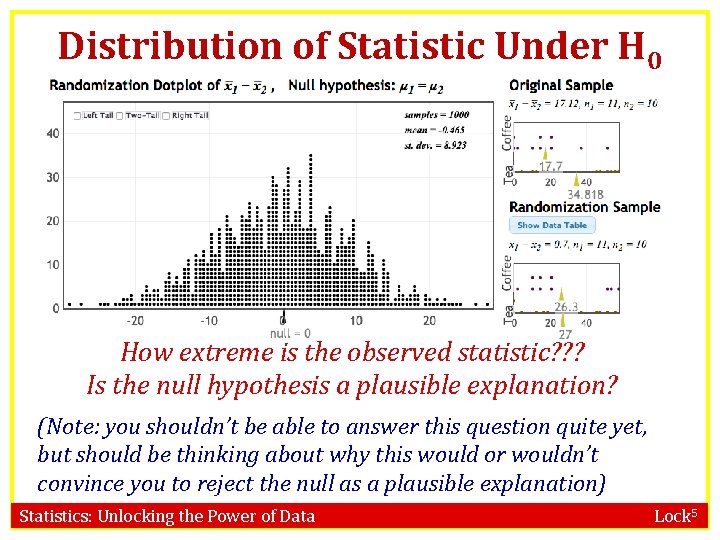
Distribution of Statistic Under H 0 How extreme is the observed statistic? ? ? Is the null hypothesis a plausible explanation? (Note: you shouldn’t be able to answer this question quite yet, but should be thinking about why this would or wouldn’t convince you to reject the null as a plausible explanation) Statistics: Unlocking the Power of Data Lock 5

Randomization Distribution A randomization distribution is a collection of statistics from samples simulated assuming the null hypothesis is true �The randomization distribution shows what types of statistics would be observed, just by random chance, if the null hypothesis were true Statistics: Unlocking the Power of Data Lock 5

Green Tea and Prostate Cancer � A study was conducted on 60 men with PIN lesions, some of which turn into prostate cancer � Half of these men were randomized to take 600 mg of green tea extract daily, while the other half were given a placebo pill � The study was double-blind, neither the participants nor the doctors knew who was actually receiving green tea � After one year, only 1 person taking green tea had gotten cancer, while 9 taking the placebo had gotten cancer Statistics: Unlocking the Power of Data Lock 5

Green Tea and Prostate Cancer The explanatory variable is green tea extract of placebo, the response variable is whether or not the person developed prostate cancer. What statistic and parameter is most relevant? a) Mean Two categorical b) Proportion variables c) Difference in means d) Difference in proportions e) Correlation Statistics: Unlocking the Power of Data Lock 5

Green Tea and Prostate Cancer p 1 = proportion of green tea consumers to get prostate cancer p 2 = proportion of placebo consumers to get prostate cancer State the null hypotheses. a) H 0: p 1 = p 2 b) H 0: p 1 < p 2 H 0: p 1 > p 2 d) H 0: p 1 ≠ p 2 c) Statistics: Unlocking the Power of Data The null hypothesis always includes an equals sign. Lock 5

Green Tea and Prostate Cancer p 1 = proportion of green tea consumers to get prostate cancer p 2 = proportion of placebo consumers to get prostate cancer State the alternative hypotheses. a) Ha: p 1 = p 2 b) Ha: p 1 < p 2 Ha: p 1 > p 2 d) Ha: p 1 ≠ p 2 c) Statistics: Unlocking the Power of Data The alternative hypothesis is what the researchers are aiming to prove. Lock 5

Randomization Test 1. State hypotheses 2. Collect data 3. Calculate statistic: 4. Simulate statistics that could be observed, just by random chance, if the null hypothesis were true (create a randomization distribution) 5. How extreme is the observed statistic? Is the null hypothesis (random chance) a plausible explanation? Statistics: Unlocking the Power of Data Lock 5

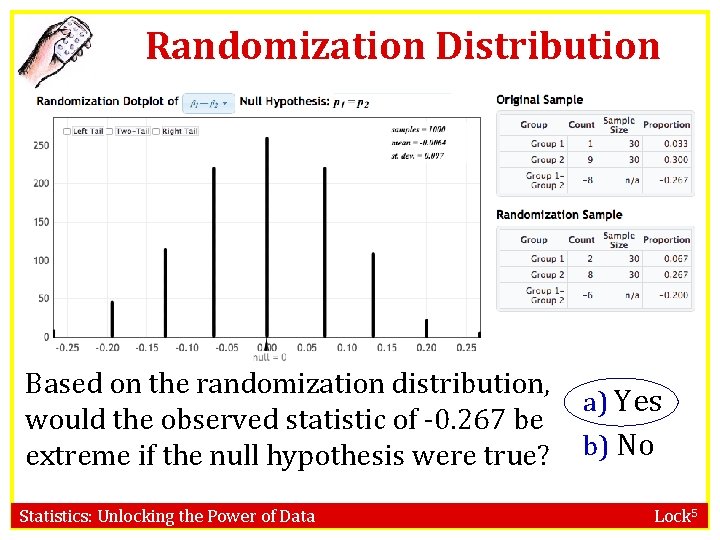
Randomization Distribution Based on the randomization distribution, a) Yes would the observed statistic of -0. 267 be extreme if the null hypothesis were true? b) No Statistics: Unlocking the Power of Data Lock 5

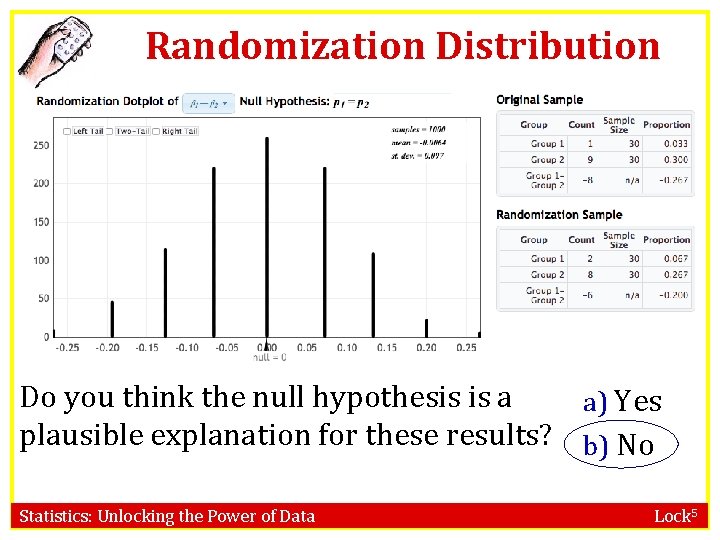
Randomization Distribution Do you think the null hypothesis is a a) Yes plausible explanation for these results? b) No Statistics: Unlocking the Power of Data Lock 5

Randomization Distribution a) Statistics: Unlocking the Power of Data We need to generate randomization samples assuming the null hypothesis is true. Lock 5

Randomization Distribution a) 10. 2 b) 12 c) 45 d) 1. 8 Statistics: Unlocking the Power of Data Randomization distributions are always centered around the null hypothesized value. Lock 5

Randomization Distribution Center �A randomization distribution simulates samples assuming the null hypothesis is true, so A randomization distribution is centered at the value of the parameter given in the null hypothesis. Statistics: Unlocking the Power of Data Lock 5

Randomization Distribution a) b) c) d) e) We want to see how extreme the observed statistic is. How extreme 10. 2 is How extreme 12 is How extreme 45 is What the standard error is How many randomization samples we collected Statistics: Unlocking the Power of Data Lock 5

Randomization Distribution a) Statistics: Unlocking the Power of Data We need to generate randomization samples assuming the null hypothesis is true. Lock 5

Randomization Distribution a) 0 b) 1 c) 21 d) 26 e) 5 Statistics: Unlocking the Power of Data The randomization distribution is centered around the null hypothesized value, 1 - 2 = 0 Lock 5

Randomization Distribution a) The standard error b) The center point c) How extreme 26 is d) How extreme 21 is e) How extreme 5 is Statistics: Unlocking the Power of Data We want to see how extreme the observed difference in means is. Lock 5

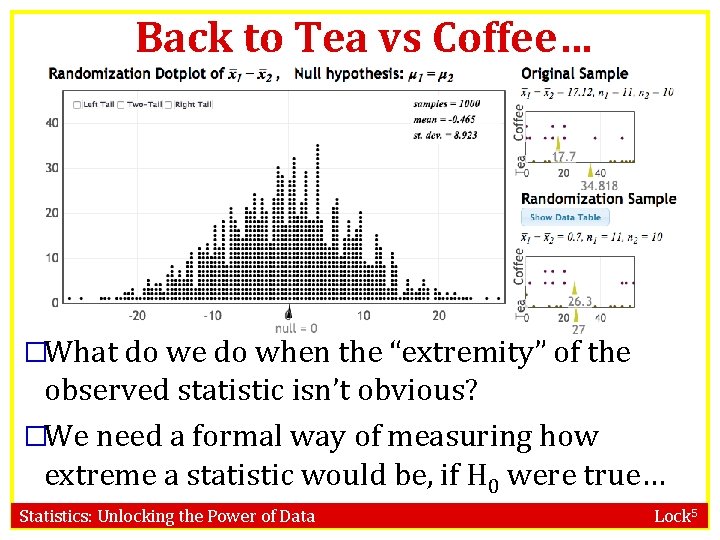
Back to Tea vs Coffee… �What do we do when the “extremity” of the observed statistic isn’t obvious? �We need a formal way of measuring how extreme a statistic would be, if H 0 were true… Statistics: Unlocking the Power of Data Lock 5

p-value The p-value is the proportion of samples, when the null hypothesis is true, that would give a statistic as extreme as (or more extreme than) the observed sample. Statistics: Unlocking the Power of Data Lock 5

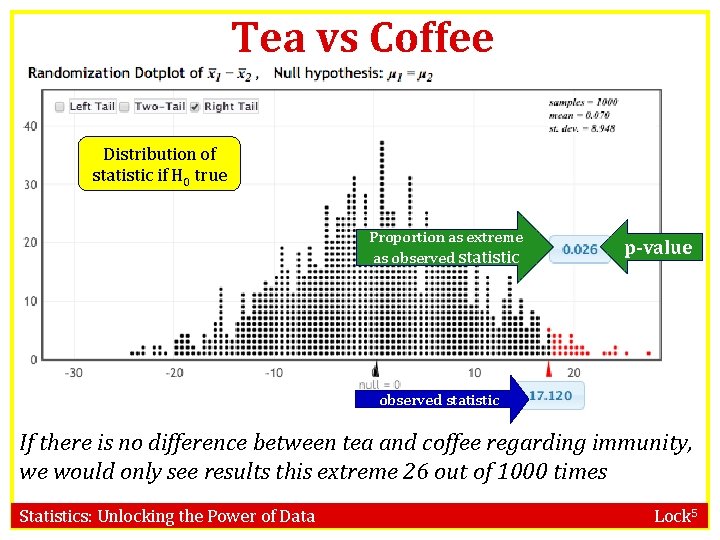
Tea vs Coffee Distribution of statistic if H 0 true Proportion as extreme as observed statistic p-value observed statistic If there is no difference between tea and coffee regarding immunity, we would only see results this extreme 26 out of 1000 times Statistics: Unlocking the Power of Data Lock 5

Calculating a p-value 1. What kinds of statistics would we get, just by random chance, if the null hypothesis were true? (randomization distribution) 2. What proportion of these statistics are as extreme as our original sample statistic? (p-value) Statistics: Unlocking the Power of Data Lock 5

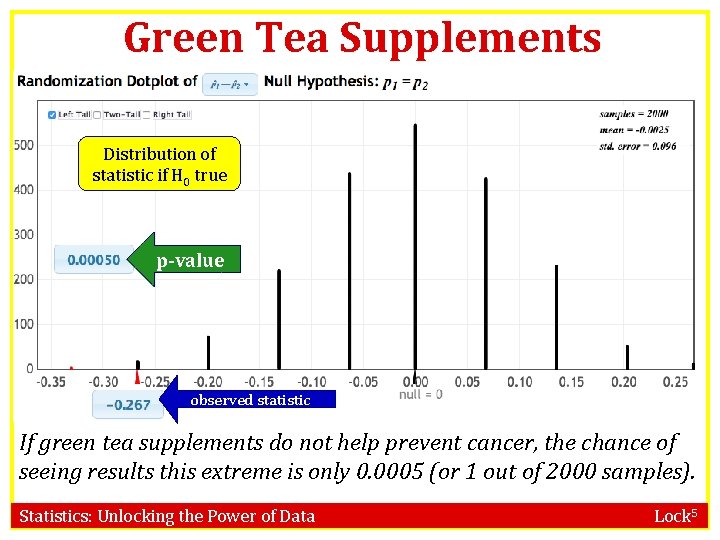
Green Tea Supplements Distribution of statistic if H 0 true p-value observed statistic If green tea supplements do not help prevent cancer, the chance of seeing results this extreme is only 0. 0005 (or 1 out of 2000 samples). Statistics: Unlocking the Power of Data Lock 5

p-value Use the randomization distribution below to test H 0 : = 0 vs Ha : > 0 Match the sample statistics: r = 0. 1, r = 0. 3, and r = 0. 5 With the p-values: 0. 005, 0. 15, and 0. 35 Which sample statistic goes with which p-value? Statistics: Unlocking the Power of Data Lock 5

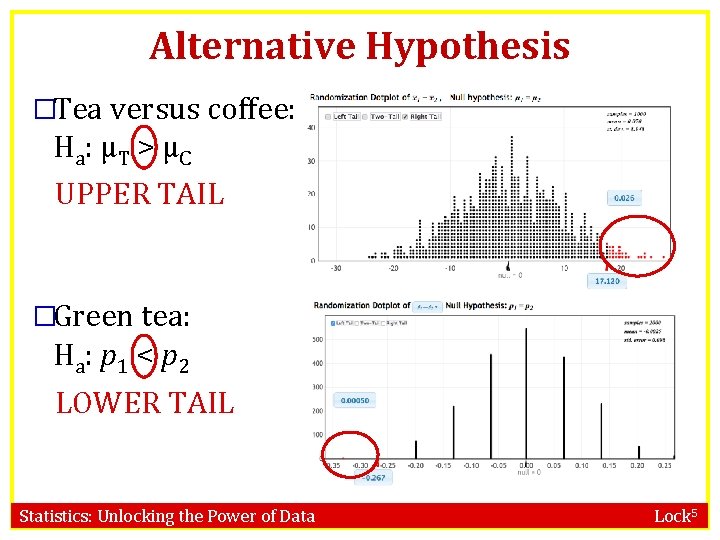
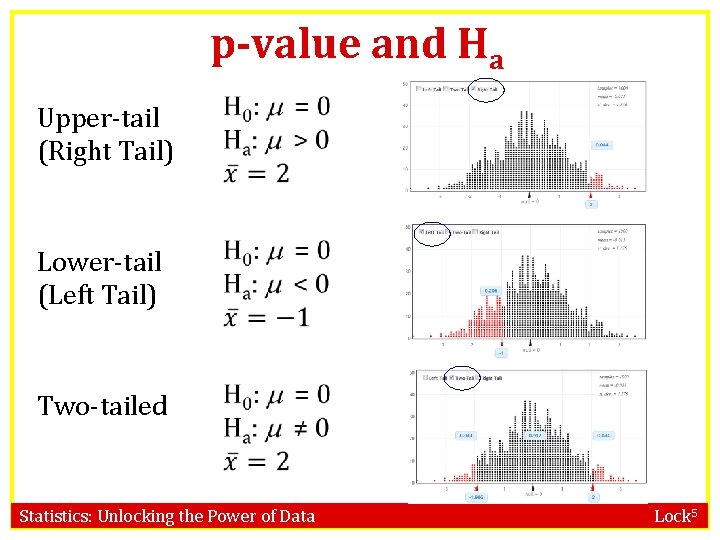
Alternative Hypothesis �Tea versus coffee: Ha: µT > µC UPPER TAIL �Green tea: Ha: p 1 < p 2 LOWER TAIL Statistics: Unlocking the Power of Data Lock 5

Alternative Hypothesis • A one-sided alternative contains either > or < • A two-sided alternative contains ≠ • The p-value is the proportion in the tail in the direction specified by Ha • For a two-sided alternative, the p-value is twice the proportion in the smallest tail Statistics: Unlocking the Power of Data Lock 5

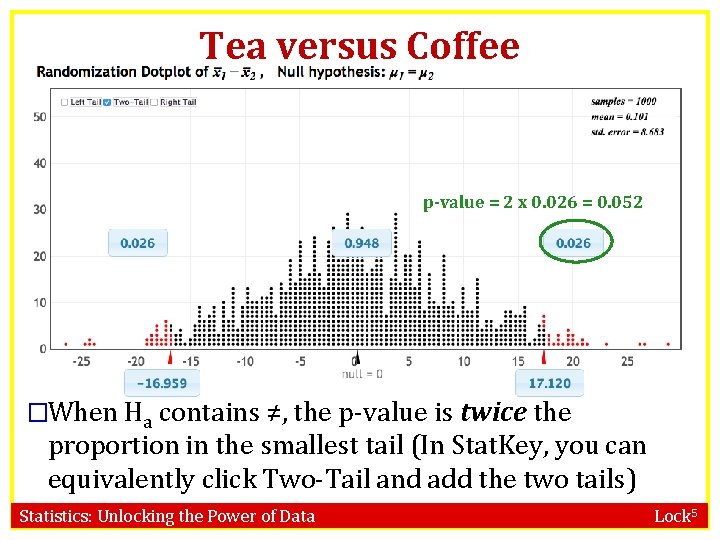
Tea versus Coffee In the tea versus coffee example, suppose instead of asking whether tea boosts immunity, the study was designed to investigate whether tea or coffee is better for the immune system. State the alternative hypothesis: a) Ha: µT = µC b) Ha: µT < µC Ha: µT > µC d) Ha: µT ≠ µC c) Statistics: Unlocking the Power of Data No specific direction is specified in the question of interest. Lock 5

Tea versus Coffee p-value = 2 x 0. 026 = 0. 052 �When Ha contains ≠, the p-value is twice the proportion in the smallest tail (In Stat. Key, you can equivalently click Two-Tail and add the two tails) Statistics: Unlocking the Power of Data Lock 5

p-value and Ha Upper-tail (Right Tail) Lower-tail (Left Tail) Two-tailed Statistics: Unlocking the Power of Data Lock 5

Warning: Check Order of Groups! �The p-value can be calculated based on the direction of the alternative hypothesis, as long as the order in Ha matches the order when the statistic is calculated! �As a check, remember that if the data support the alternative hypothesis, the p-value of a onesided test should not be more than 0. 5! Statistics: Unlocking the Power of Data Lock 5

Summary • The randomization distribution shows what types of statistics would be observed, just by random chance, if the null hypothesis were true • A p-value is the chance of getting a statistic as extreme as that observed, if H 0 is true • A p-value can be calculated as the proportion of statistics in the randomization distribution as extreme as (or more extreme than) the observed sample statistic Statistics: Unlocking the Power of Data Lock 5