Section 3 6 Solving Systems of Linear Equations



















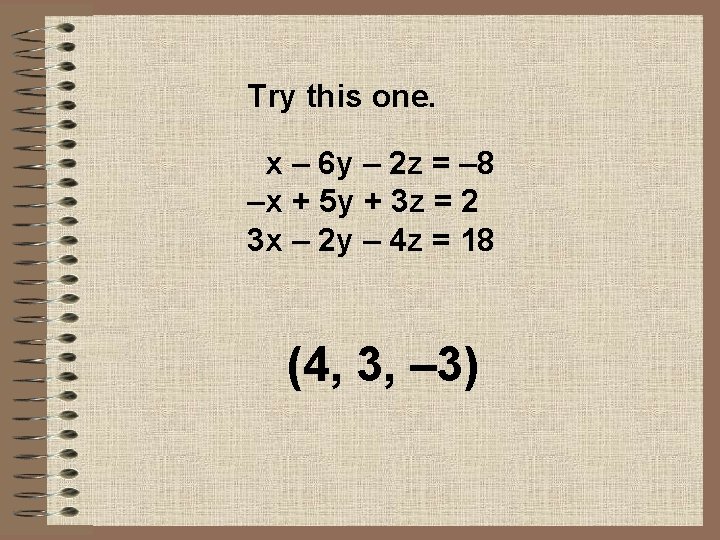



- Slides: 24

Section 3. 6 – Solving Systems of Linear Equations in Three Variables

A linear equation in three variables x, y, and z is an equation of the form Ax + By + Cz = d, where a, b, and c are not all zero. The following is an example of a system of three linear equations in three variables: 2 x + y – z = 5 3 x – 2 y + z = 16 4 x + 3 y – 5 z = 3

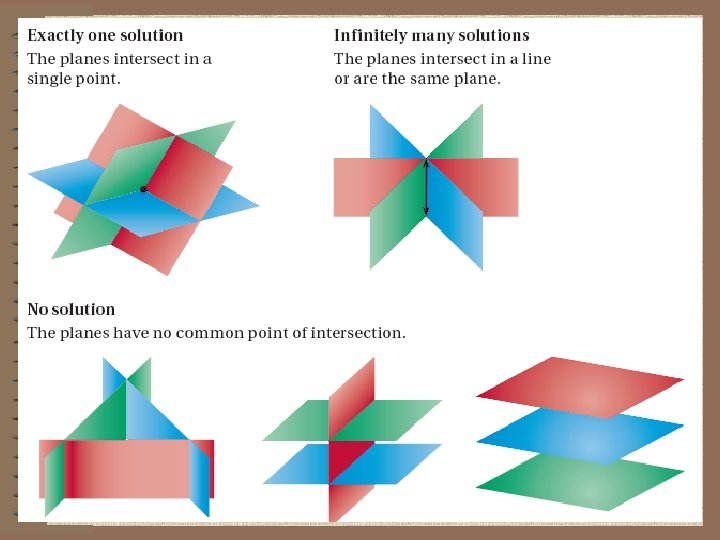
A solution of such a system is an ordered triple (x, y, z) whose coordinates make each equation true. The graph of a linear equation in three variables is a plane in three-dimensional space. The graphs of three such equations that form a system are three planes whose intersection determines the number of solutions of the system.



Use elimination to solve the following system of equations. x – 3 y + 6 z = 21 3 x + 2 y – 5 z = – 30 2 x – 5 y + 2 z = – 6

Step 1 Rewrite the system as two smaller systems, each containing two of the three equations.


Step 2 Eliminate THE SAME variable in each of the two smaller systems. Any variable will work, but sometimes one may be a bit easier to eliminate. Choose x for this system.


Step 3 Write the resulting equations in two variables together as a system of equations. Solve the system for the two remaining variables.

11 y – 23 z = – 93 y – 10 z = – 48 (– 11) 11 y – 23 z = – 93 – 11 y + 110 z = 528 87 z = 435 z=5 y – 10(5) = – 48 y – 50 = – 48 y=2

Step 4 Substitute the value of the variables from the system of two equations in one of the ORIGINAL equations with three variables.

x – 3 y + 6 z = 21 3 x + 2 y – 5 z = – 30 2 x – 5 y + 2 z = – 6 Use the first equation. x – 3(2) + 6(5) = 21 x – 6 + 30 = 21 x + 24 = 21 x = – 3

Step 5 CHECK the solution in ALL 3 of the original equations. Write the solution as an ordered triple


Equation 1 Solve this system Equation 2 -3 2 Equation 3 Multiply Eq. 2 by 2 and add it to Eq. 1. Save this result Solve this new system of linear equation in two variables. Multiply the bottom eq. by 7 and add it to the top eq. 7 x +10 z = 19 Now multiply Eq. 2 by -3 and add it to Eq. 3. Save this result. -18 z = -72 or z = 4 Substituting z=4 into either of the new equations will give x = -3……finally substituting these values into any of the original equations give y = 2. -x -4 z = -13 Our final solution is (-3, 2, 4)

Here is a system with No Solution. Equation 1 Equation 2 Equation 3 Add -3 times Eq 1 to Eq 2. 0=8 Since this is a false equation, you can conclude the original system of equations has no solution.

Here is a system with MANY solutions Equation 1 Equation 2 Equation 3 Add Eq. 1 to Eq. 2 2 x + 2 y =4 New EQ. 1 Add Eq 2 to Eq 3 3 x +3 y =6 New EQ 2 Solving this new system of two equation by adding -3 times the first eq. to 2 times the second eq. produces the identity 0 = 0. So, the system has infinitely many solution.

Substitution Method Since x+y=z, substitute this for z in the first two equations Simplify Finally, solve this linear system of two equations and two variables to get x = 4 and y =8 Since z=x+y, z = 12. Our final solution is (4, 8, 12)
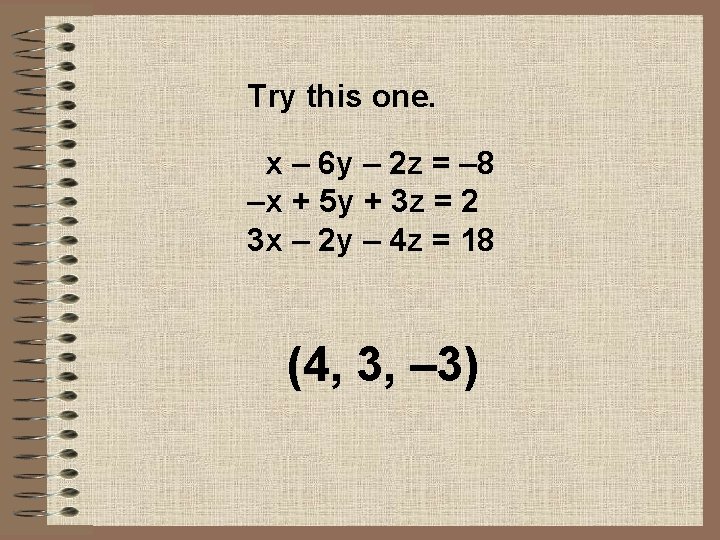
Try this one. x – 6 y – 2 z = – 8 –x + 5 y + 3 z = 2 3 x – 2 y – 4 z = 18 (4, 3, – 3)

– 5 x + 3 y + z = – 15 10 x + 2 y + 8 z = 18 15 x + 5 y + 7 z = 9 (1, – 4, 2)

Example 2: Solve the system: 2 x – y + 6 z = -4 6 x + 4 y – 5 z = -7 -4 x – 2 y + 5 z = 9

Example 3: Solve the system: x+y+z=3 4 x + 4 y + 4 z = 7 3 x – y + 2 z = 5