Section 3 6 Reciprocal Functions Objectives 1 To

Section 3. 6 Reciprocal Functions

Objectives: 1. To identify vertical asymptotes, domains, and ranges of reciprocal functions. 2. To graph reciprocal functions.

Definition Reciprocal Function Any function that is a reciprocal of another function.

Definition Reciprocal trigonometric ratios: 1 1 secx = cscx = cos x sin x 1 cotx = tan x

Definition Reciprocal trigonometric functions: y = sec y = csc y = cot

These functions are examples of a larger class of reciprocal functions, including reciprocals of power, polynomial, and exponential functions.

Examples of reciprocal functions 1 1 f(x) = 4 g(x) = 2 3 x x – 4 1 h(x) = x 4 k(x) = sec x

EXAMPLE 1 Find f(1), g(2), h(1/2), and k( /4), using the functions 1 above. f(x) = 4 3 x 1 1 f(1) = 4 = 3(1) 3

EXAMPLE 1 Find f(1), g(2), h(1/2), and k( /4), using the functions 1 above. g(x) = 2 x – 4 1 1 g(2) = 2 – 4 0 undefined , which is

EXAMPLE 1 Find f(1), g(2), h(1/2), and k( /4), using the functions 1 above. h(x) = x 4 1 1 1 h( /2) = 1/2 = 4 4 1 = 2

EXAMPLE 1 Find f(1), g(2), h(1/2), and k( /4), using the functions above. k(x) = sec x k( / 4) = sec / 2 = =2 2 1 = / 4 cos 4 1 = 2/ 2

Since reciprocal functions have denominators, you must be careful about what values are used in the domain.

EXAMPLE 2 Find the domains of f(x), g(x), h(x), and k(x) in the previous functions. Find all values for which the denominator of f(x) and g(x) equals f(x) zero. g(x) 3 x 4 = 0 x 2 – 4 = 0 x 2 = 4 x=0 x = ± 2

EXAMPLE 2 Find the domains of f(x), g(x), h(x), and k(x) in the previous functions. Exclude those values from the domain. f(x): D = {x|x R, x ≠ 0} g(x): D = {x|x R, x ≠ ± 2}

EXAMPLE 2 Find the domains of f(x), g(x), h(x), and k(x) in the previous functions. Since 4 x ≠ 0 x, the domain of h(x) is R. cos x = 0 when x = /2 + k , Since k R, the domain of k(x) is D = {x|x R, x ≠ /2 + k , k Z}.

1 EXAMPLE 3 Graph g(x) =2. x – 4 Give the domain and range. Is g(x) continuous? Is g(x) an odd or even function?

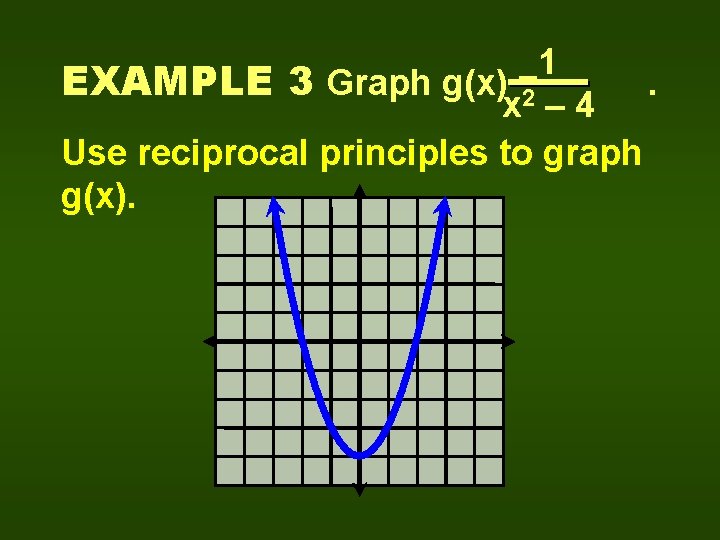
1 EXAMPLE 3 Graph g(x) =2. x – 4 Use reciprocal principles to graph g(x).

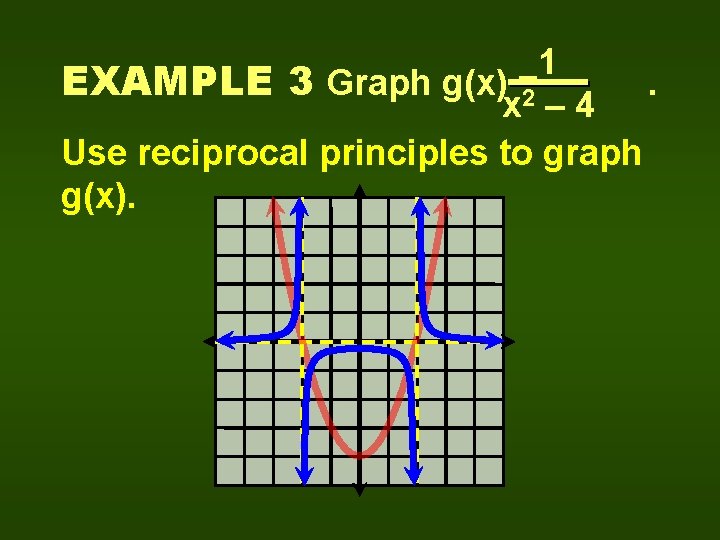
1 EXAMPLE 3 Graph g(x) =2. x – 4 Use reciprocal principles to graph g(x).

1 EXAMPLE 3 Graph g(x) =2 x – 4 D = {x|x ≠ ± 2} R = {y|y 0 or y -1/4} g(x) is an even function but is not continuous. .

1 EXAMPLE 4 Graph g(x) =2 x – 4 again without graphing its reciprocal function first. 1. Find the domain excluding values where the denominator equals zero. x 2 – 4 = 0 x 2 = 4 x = ± 2 D = {x|x ≠ ± 2} .

1 EXAMPLE 4 Graph g(x) =2. x – 4 again without graphing its reciprocal function first. 2. Check for x-intercepts. Since the numerator cannot equal zero, the graph cannot touch the x-axis.

1 EXAMPLE 4 Graph g(x) =2. x – 4 again without graphing its reciprocal function first. 3. Plot a point in each of the regions determined by the asymptotes (2 & -2). Since the graph cannot cross the xaxis, points within a region will all be on the same side of the x-axis. Include the y-

1 EXAMPLE 4 Graph g(x) =2. x – 4 again without graphing its reciprocal function first. 4. Use the asymptotes as guides. Your graph will never quite reach either vertical asymptote or the x-axis.

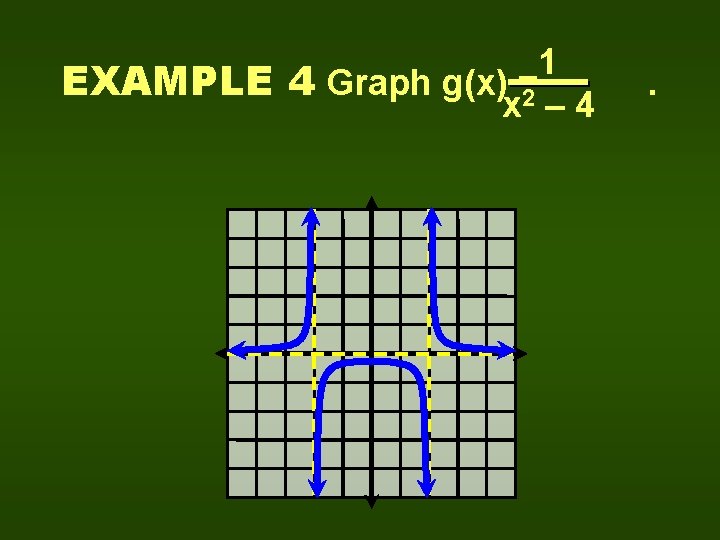
1 EXAMPLE 4 Graph g(x) =2 x – 4 .

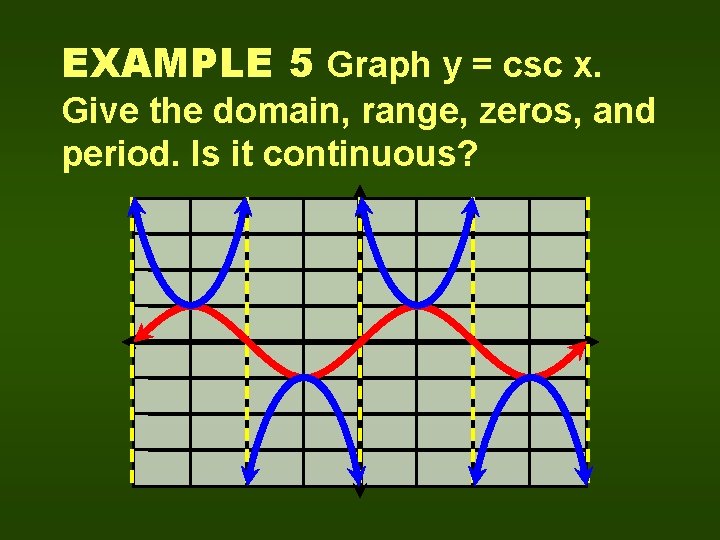
EXAMPLE 5 Graph y = csc x. Give the domain, range, zeros, and period. Is it continuous?

EXAMPLE 5 Graph y = csc x. Give the domain, range, zeros, and period. Is it continuous? D = {x|x ≠ k , k Z} R = {y|y 1 or y -1} The function has no zeros; the period is 2. It is not continuous.

Homework: pp. 148 -151

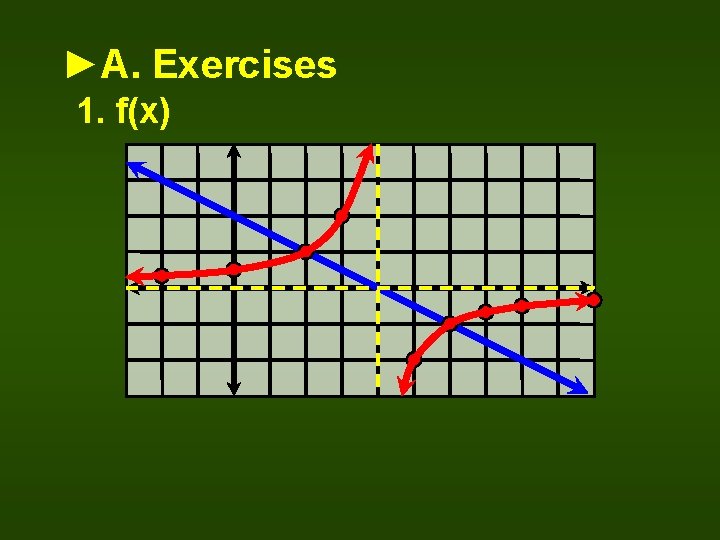
►A. Exercises 1. f(x)

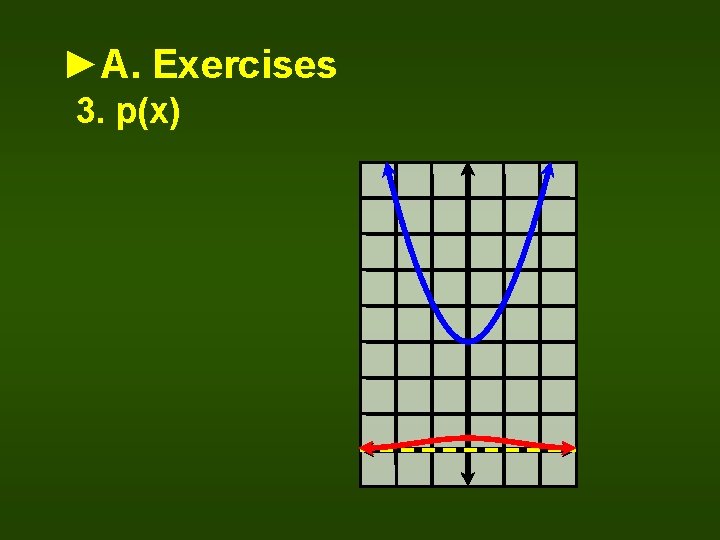
►A. Exercises 3. p(x)

►A. Exercises 6. Give the vertical asymptotes of 1 h(x) = 2 x + 5 x – 14

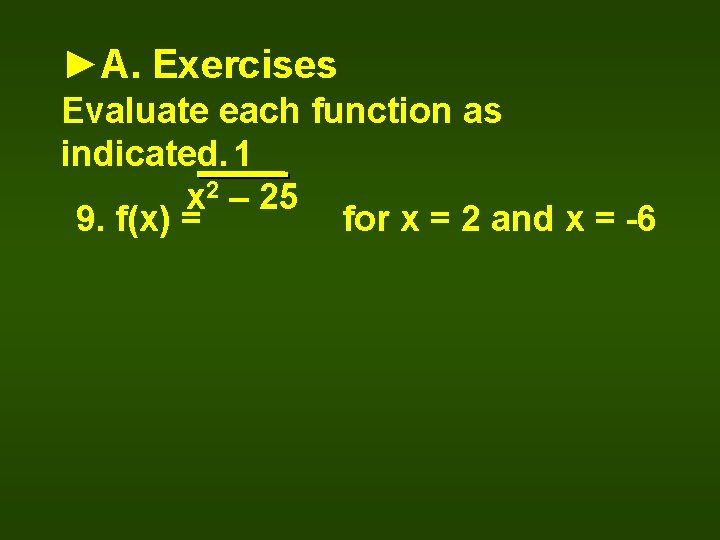
►A. Exercises Evaluate each function as indicated. 1 x 2 – 25 9. f(x) = for x = 2 and x = -6

►B. Exercises 12. Graph the reciprocal function. Give the domain and range. 1 h(x) = 2 x + 5 x – 14

■ Cumulative Review 41. Solve ABC where A = 58°, B = 39°, and a = 10. 5.

■ Cumulative Review 42. Give the period and amplitude of y = 5 sin 3 x.

■ Cumulative Review 43. Find f(4) if x – 8 if x 3 2 f(x) = x – 1 if 3 x 9 7 x if x 9

■ Cumulative Review 44. How many zeros does a cubic polynomial function have? Why?

■ Cumulative Review 45. Graph y = 2 x and estimate 20. 7 from the graph.

A summary of principles for graphing reciprocal functions follows: 1. The larger the number, the closer the reciprocal is to zero. 2. The reciprocal of 1 and -1 is itself. 3. There is a vertical