Section 3 5 Equivalent Statements Variations of Conditional

Section 3. 5 Equivalent Statements, Variations of Conditional Statements, and De Morgan’s Laws Objectives 1. Use a truth table to show that statements are equivalent. 2. Write the equivalent contrapositive for a conditional statement. 3. Write the converse and inverse of a conditional statement. 4. Write the negation of a conditional statement. 5. Use De Morgan’s laws. 12/29/2021 Section 3. 5 1

Equivalent Statements • Equivalent compound statements are made up of the same simple statements and have the same corresponding truth values for all true-false combinations of these simple statements. – If a compound statement is true, then its equivalent statement must also be true. – If a compound statement is false, its equivalent statement must also be false. • A special symbol is used to show two statements are equivalent. 12/29/2021 Section 3. 5 2

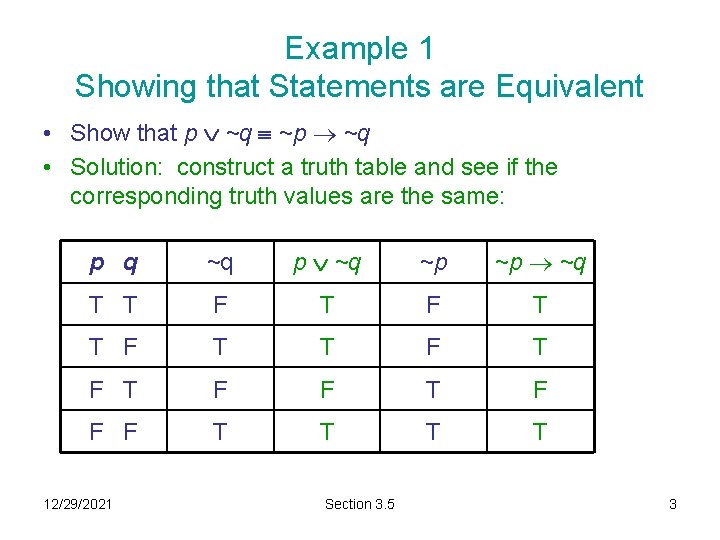
Example 1 Showing that Statements are Equivalent • Show that p ~q ~p ~q • Solution: construct a truth table and see if the corresponding truth values are the same: p q ~q p ~q ~p ~p ~q T T F T F F F T T 12/29/2021 Section 3. 5 3

The Contrapositive of the Conditional Statement p q • A conditional statement and its equivalent contrapositive: p q ~p • The truth value of a conditional statement does not change if the antecedent and consequent are reversed and both are negated: • ~q ~p is called the contrapositive of the conditional p q. 12/29/2021 Section 3. 5 4

Example 2 Writing Equivalent Contrapositives Write the equivalent contrapositive for: a. If you live in Los Angeles, then you live in California p: You live in Los Angeles. q: You live in California. If you live in Los Angeles, then you live in California. p q If you do not live in California, then you do not live in Los Angeles. ~q 12/29/2021 ~p Section 3. 5 5

Variations of the Conditional Statement Name Symbolic Form Conditional p q Converse q p Inverse ~p ~q Contrapositive ~ q ~p English Translation If p then q If q then p If not p, then not q If not q, then not p Conditional and Contrapositive are equivalent. Converse and Inverse are equivalent. 12/29/2021 Section 3. 5 6

Example 3 Writing Variations of a Conditional Statement • Write the converse, inverse, and contrapositive of the following conditional statement: If it’s a lead pencil, then it does not contain lead. (true) • Solution: Use the following representations: p: It’s a lead pencil. q: It contains lead. 12/29/2021 Section 3. 5 7

Example 3 continued • Now work with p ~q to form the converse, inverse and contrapositive. • Then translate the symbolic form of each statement back into English. 12/29/2021 Section 3. 5 8

Example 4 The Negation of a Conditional Statement • The negation of p q is p ~q. This can be expressed as: ~(p q) p ~ q • Write the negation of: If too much homework is given, a class should not be taken. • Solution: p: Too much homework is given q: A class should be taken The symbolic form is p ~q 12/29/2021 Section 3. 5 9

Example 4 continued • The negation of p ~q is p ~(~ q) which simplifies to p q. • Translating into English: Too much homework is given and a class should be taken. 12/29/2021 Section 3. 5 10

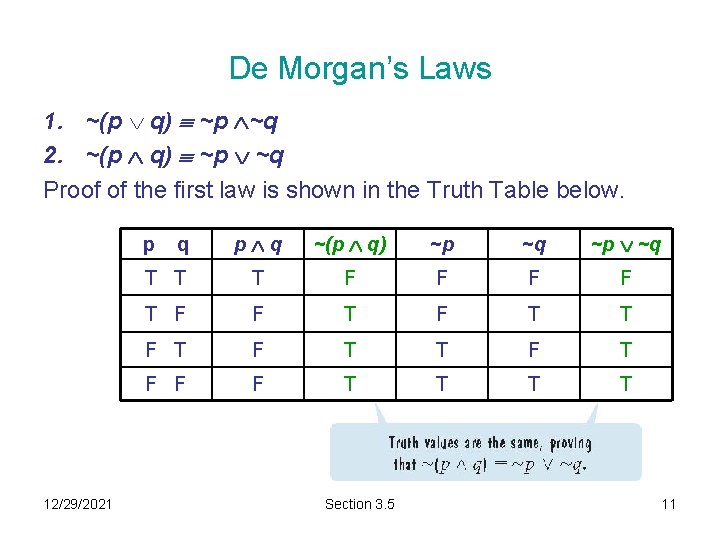
De Morgan’s Laws 1. ~(p q) ~p ~q 2. ~(p q) ~p ~q Proof of the first law is shown in the Truth Table below. p q ~(p q) ~p ~q ~p ~q T T T F F T F T F F F T T p 12/29/2021 q Section 3. 5 11

De Morgan’s Laws and Negations 1. ~(p q) ~p ~q The negation of p q is ~(p q). To negate a conjunction, negate each component statement and change and to or. 2. ~(p q) ~p ~q. The negation of p q is ~p ~q. To negate a disjunction, negate each component statement and change or to and. 12/29/2021 Section 3. 5 12

Example 5 Negating Conjunctions and Disjunctions • Write the negation for each of the following statements: a. All students do laundry on weekends and I do not. b. Some college professors are entertaining lecturers or I’m bored. 12/29/2021 Section 3. 5 13