Section 3 4 Permutations Combinations 1 Permutations A

Section 3. 4 Permutations & Combinations 1

Permutations: A permutation is an ordered arrangement of objects. (without repetition) e. g. # of 4 -digit numbers without repeated digits 10 9 8 7 (using multiplication principle) # of permutations of r distinct objects chosen from n distinct objects. 2

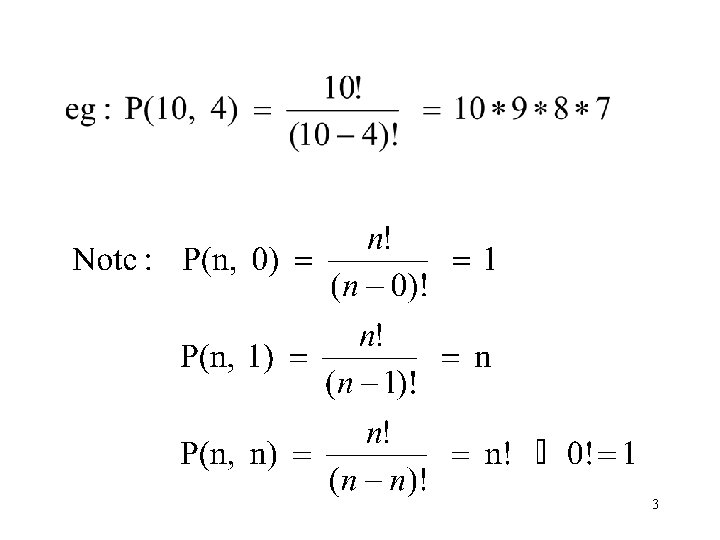
3

e. g. How many 3 -letter words(not necessarily meaningful) can be formed from the word “Compiler” if no letter can be repeated? e. g. How many ways can a president and vice-president be selected from a group of 20 people? 4

Combinations: a combination is an unordered arrangement of objects. (without repetition) 5

e. g. How many 5 -card poker hands can be dealt from a 52 -card deck? (note that the order here doesn’t matter) 6

e. g. A committee of 8 students is to be selected from a class consisting of 19 freshmen and 34 sophomores. a) In how many ways can 3 freshmen and 5 sophomores be selected? b) In how many ways can a committee with c) exactly 1 freshman be selected? 7

c) In how many ways can a committee with d) at most 1 freshman be selected? e) In how many ways can a committee with f) at least 1 freshman be selected? 8

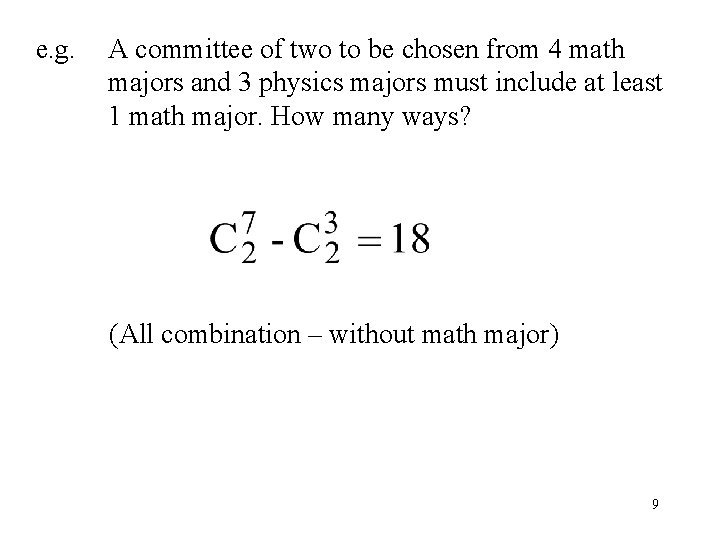
e. g. A committee of two to be chosen from 4 math majors and 3 physics majors must include at least 1 math major. How many ways? (All combination – without math major) 9

Relations: P(n, r) = C(n, r) P(r, r) (Obvious) C(n, r) = C(n, n-r) (Obvious) C(n, r) = C(n-1, r-1) + C(n-1, r) (Why? ) Proof: 10

Consider a 5 -card hand from a 52 -card deck: 1) How many hands consist of all diamonds? 2) How many hands consist of all the same suit? 3) How many hands contain three of a kind? 4) exactly 3 of a kind + exactly 4 of a kind 4) How many hands contain a full house? 5) (3 of a kind with a pair) 11

P(n, r) and C(n, r) assume that each object will only be selected once. (w/o repetition) Now, suppose n objects are available for reuse: (w/repetition) – permutations of r objects out from n objects with repetition is easy: for 1 st object: n choices nr nd 2 object: still n choices arrangements … rth object: n choices 12

– Combinations of r objects out from n objects w/repetition: e. g. a jeweler is designing a pin with 5 stones chosen from diamonds, rubies and emeralds. How many ways can the stones be selected? (n = 3, r = 5) (we want the number of combinations of five objects out of 3 objects with repetition allowed) | | : 1 diamond, 3 rubies, 1 emeralds ||: 5 diamonds this problem is transformed to choosing 2 positions for bars out from 7(or choosing 5 positions for out from 7 ) in general: n objects need (n-1) markers, so Positions r Positions for Objects 13

e. g. How many distinct permutations can be made from the characters in word FLORIDA? all characters are distinct, (no selection here, we want all 7 characters): 7! 14

e. g. How many distinct permutations can be made from the characters in word MISSISSIPPI? It’s not 11! MIS 1 S 2 ISSIPPI = MIS 2 S 1 ISSIPPI, need to eliminate duplicates: 4 S’s occupy 4 positions in the string, but the arrangement among these 4 S’s does not matter, how many permutations of 4 S’s? 4 3 2 1 = 4! Similarly, 4 I’s has 4! undistinguished permutations, 2 P’s has 2! undistinguished permutations, 15