Section 3 4 Measures of Relative Standing and





















- Slides: 24

Section 3 -4 Measures of Relative Standing and Boxplots Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 1

Key Concept This section introduces measures of relative standing, which are numbers showing the location of data values relative to the other values within a data set. They can be used to compare values from different data sets, or to compare values within the same data set. The most important concept is the z score. We will also discuss percentiles and quartiles, as well as a new statistical graph called the boxplot. Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 2

Part 1 Basics of z Scores, Percentiles, Quartiles, and Boxplots Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 3

Z score v z Score (or standardized value) the number of standard deviations that a given value x is above or below the mean Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 4

Measures of Position z Score Sample x – x z= s Population x – µ z= Round z scores to 2 decimal places Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 5

Interpreting Z Scores Whenever a value is less than the mean, its corresponding z score is negative Ordinary values: – 2 ≤ z score ≤ 2 Unusual Values: z score < – 2 or z score > 2 Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 6

Z score example • Let’s work problem 6 on page 127 • Phillip Seymour Hoffman was 38 years of age when he won a Best Actor Oscar for his role in Capote. The Oscar-winning Best Actors have a mean age of 43. 8 years and a standard deviation of 8. 9 years • What is the difference between Hoffman’s age and the mean age? • How many standard deviations is that? • Convert Hoffman’s age to a z score • Is that usual or unusual? Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 7

Percentiles are measures of location. There are 99 percentiles denoted P 1, P 2, . . . P 99, which divide a set of data into 100 groups with about 1% of the values in each group. Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 8

Finding the Percentile of a Data Value Percentile of value x = number of values less than x total number of values Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. • 100 3. 1 - 9

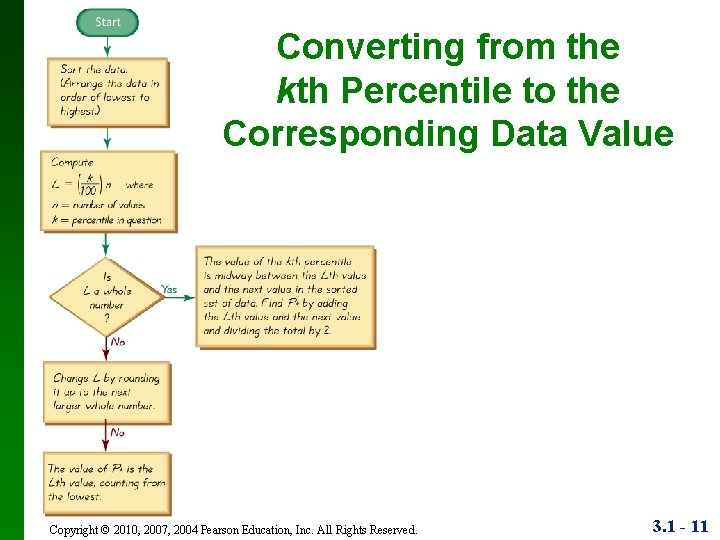
Converting from the kth Percentile to the Corresponding Data Value Notation L= k 100 • n total number of values in the data set k percentile being used L locator that gives the position of a value Pk kth percentile n Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 10

Converting from the kth Percentile to the Corresponding Data Value Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 11

Percentile Problem • Here are combined scores for 24 Super Bowls • 36, 37, 39, 41, 43, 44, 47, 50, 53, 54, 55, 56, 57, 59, 61, 65, 69, 75 • Find the percentile corresponding to 65 points • Find the number that corresponds to the 20 th percentile (P 20) • Find P 80 Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 12

Quartiles Are measures of location, denoted Q 1, Q 2, and Q 3, which divide a set of data into four groups with about 25% of the values in each group. v Q 1 (First Quartile) separates the bottom 25% of sorted values from the top 75%. v Q 2 (Second Quartile) same as the median; separates the bottom 50% of sorted values from the top 50%. v Q 3 (Third Quartile) separates the bottom 75% of sorted values from the top 25%. Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 13

Quartiles Q 1, Q 2, Q 3 divide ranked scores into four equal parts 25% (minimum) 25% 25% Q 1 Q 2 Q 3 (maximum) (median) Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 14

Some Other Statistics v Interquartile Range (or IQR): Q 3 – Q 1 v Semi-interquartile Range: v Midquartile: Q 3 + Q 1 Q 3 – Q 1 2 2 v 10 - 90 Percentile Range: P 90 – P 10 Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 15

5 -Number Summary v For a set of data, the 5 -number summary consists of the minimum value; the first quartile Q 1; the median (or second quartile Q 2); the third quartile, Q 3; and the maximum value. Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 16

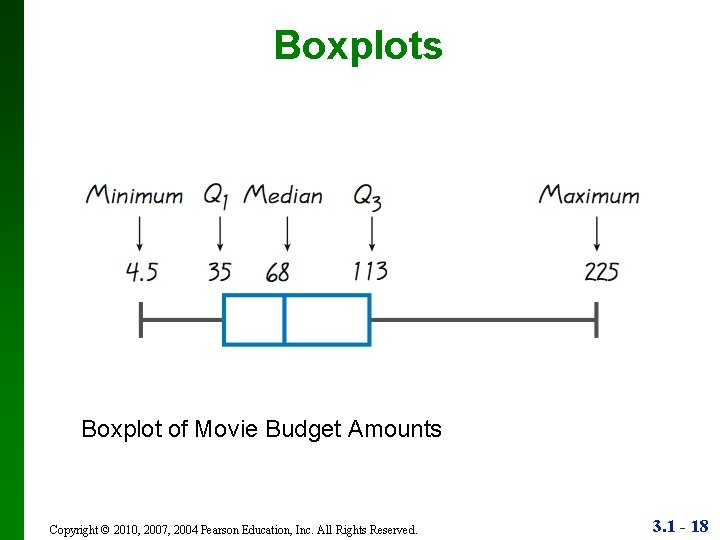
Boxplot v A boxplot (or box-and-whiskerdiagram) is a graph of a data set that consists of a line extending from the minimum value to the maximum value, and a box with lines drawn at the first quartile, Q 1; the median; and the third quartile, Q 3. Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 17

Boxplots Boxplot of Movie Budget Amounts Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 18

Percentile Problem • Here are combined scores for 24 Super Bowls • 36, 37, 39, 41, 43, 44, 47, 50, 53, 54, 55, 56, 57, 59, 61, 65, 69, 75 • Construct a box plot and include a the values of the 5 -number summary. Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 19

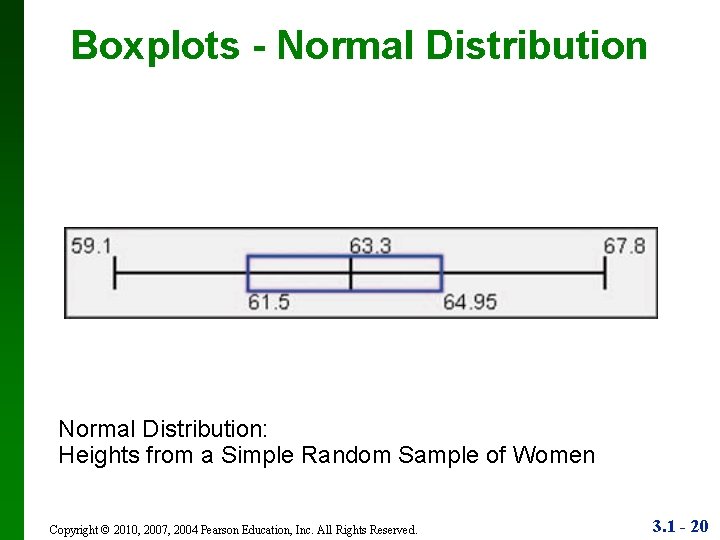
Boxplots - Normal Distribution: Heights from a Simple Random Sample of Women Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 20

Boxplots - Skewed Distribution: Salaries (in thousands of dollars) of NCAA Football Coaches Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 21

Recap In this section we have discussed: v z Scores and unusual values v Percentiles v Quartiles v Converting a percentile to corresponding data values v Other statistics v 5 -number summary Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 22

One Final Example • Scores on the SAT test have a mean of 1518 and a standard deviation of 325. Scores on the ACT test have a mean of 21. 1 and a standard deviation of 4. 8. Which is relatively better: a score of 1190 of the SAT test or a score of 16. 0 on the ACT test? Why? Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 23

Putting It All Together Always consider certain key factors: v Context of the data v Source of the data v Sampling Method v Measures of Center v Measures of Variation v Distribution v Outliers v Changing patterns over time v Conclusions v Practical Implications Copyright © 2010, 2007, 2004 Pearson Education, Inc. All Rights Reserved. 3. 1 - 24