Section 3 3 Using Laws of Logic Using

Section 3. 3 Using Laws of Logic

Using contrapositives The negation of a hypothesis or of a conclusion is formed by denying the original hypothesis or conclusion. Statement Symbol The weather is good. I will go swimming. P q Negation Symbol The weather is not good. I will not go swimming. ~p ~q The inverse of the conditional statement p q is ~p ~q. The contrapositive of the conditional statement p q is ~q ~p.

Examples: Original Statement: p q If Polly says “Hello”, then Paul says “Hello. ” Hypothesis, p Converse: conclusion, q q p If Paul says “Hello’” then Polly says “Hello. ” Inverse: ~p ~q If Polly does not say “Hello’” then Paul does not say “Hello. ” Contrapositive: ~q ~p If Paul does not say “Hello’” then Polly does not say “Hello. ”

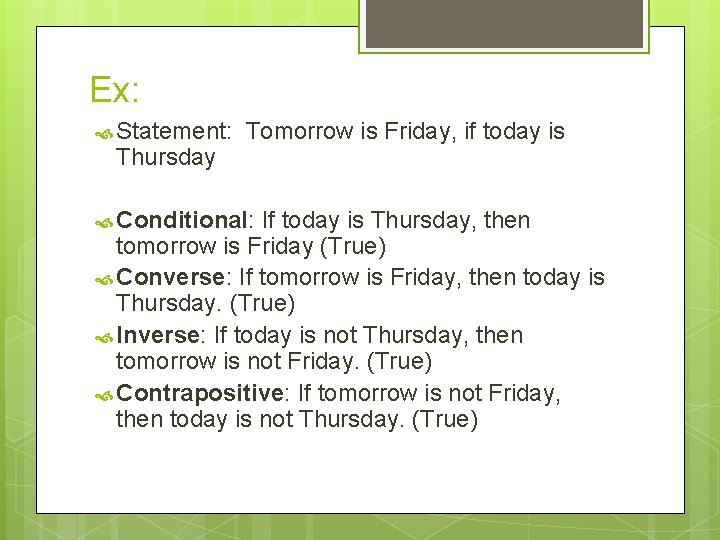
Ex: Statement: Thursday Tomorrow is Friday, if today is Conditional: If today is Thursday, then tomorrow is Friday (True) Converse: If tomorrow is Friday, then today is Thursday. (True) Inverse: If today is not Thursday, then tomorrow is not Friday. (True) Contrapositive: If tomorrow is not Friday, then today is not Thursday. (True)

Ex: Statement: A figure is a parallelogram if it is a square Conditional: If a figure is a square, then it is a parallelogram. (True) Converse: If a figure is a parallelogram, then it is a square. (False) Inverse: If a figure is not a square, then it is not a parallelogram. (False) Contrapositive: If a figure is not a parallelogram, then it is not a square. (True)

Summary Statement If p, then q. Converse If q, then p. Inverse If not p, then not q. Contrapositive If not q, then not p. An important fact to remember about the contrapositive, is that it always has the SAME truth value as the original conditional statement. **If the original statement is TRUE, the contrapositive is TRUE. If the original statement is FALSE, the contrapositive is FALSE. They are said to be logically equivalent.

Laws of Logical Reasoning Law of Syllogism (like transitive property) “If p then q, if q then r therefore if p then r” p q q r Therefore, p r Ex: If today is Tuesday, then I have gym. If I have gym, then I wear my sneakers. Conclusion using law of syllogism: If today is Tuesday, then I wear my sneakers.

Laws cont. Law of Detachment(ordering steps to reach conclusion) p q P is true Therefore, q is true Ex: Given <1 = 50° A) if <1= 50°, then <2= 40° B) if <3= 40°, then <4= 140° C) if <4= 140°, then <5= 140° D) <1 = 50° E) if <2= 40°, then <3= 40° Solution: order of steps D, A, E, B, C Conclusion using law of detachment: <5 = 140°