Section 3 3 Percentiles and BoxandWhisker Plots Stats

Section 3. 3 Percentiles and Box-and-Whisker Plots

Stats Wednesday, November 7 Check – in homework “Empirical Rule & Chebyshev’s Theorem” Worksheets Notes – Section 3. 3 Percentiles 5 -Number Summaries Box – and Whisker Plots Thursday: Quiz – Section 3. 2 Friday: Review for Chapter 3 Test Work on Assignment Monday: Chapter 3 Test

Objectives After this section, you will be able to: Interpret the meaning of percentile scores; Compute the median, quartiles, and five-number summary from raw data; Make a box-and-whisker plot. Interpret the results; Describe how a box-and-whisker plot indicates spread of data about the median.

Percentile For whole numbers P ( where 1 ≤ P ≤ 99), the Pth percentile of a distribution is a value such the _____ of the data fall ____________ it and (100 – P)% of the data fall at or __________. See Figure 3 -3 on pg 103 “A Histogram with the 60 th Percentile”

Guided Exercise You took the English achievement test to obtain college credit in freshman English by exam. If your score is at the 89 th percentile, what percentage of scores are at or below yours? If the scores ranged from 1 to 100 and your raw score is 95, does this necessarily mean that your score is at the 95 th percentile?

Calculating Percentiles There are _____ percentiles. In an ideal situation, the ____ percentiles divide the data into _____ equal parts. 1% Lowest 1% 1 st 1% 2 nd 1% 3 rd 1% 4 th … 5 th 1% 1% 98 th 1% 99 th If the number of data points are not exactly divisible by _______, the percentiles ______________________. Highest

Special Percentiles…. Quartiles divide the data into __________. Quartile 1: Quartile 2: Quartile 3:

How to Compute Quartiles 1. Order the data from smallest to largest; 2. Find the median. This is _____. 3. Find Q 1 = the median of the ___________ of the data (not including Q 2). 4. Find Q 3 = the median of the ___________ of the data (not including Q 2).

Interquartile range IQR = _______________ …tells us the _______ of the middle half of the data.

Example Consumer Reports did a study of ice cream bars. 27 bars with taste ratings of the least “fair” were listed, and cost per bar was included in the report. Just how much will an ice cream bar cost? Bar sizes varied. Cost of Ice Cream Bars (in dollars) 0. 99 1. 07 1. 00 0. 50 0. 37 1. 03 1. 07 0. 97 0. 63 0. 33 0. 50 0. 97 1. 08 0. 47 0. 84 1. 23 0. 25 0. 50 0. 40 0. 33 0. 35 0. 17 0. 38 0. 20 0. 18 0. 16 A. Find the quartiles. B. Find the Interquartile range.

A. Find the Quartiles 1. First, order the data from smallest to largest. Ordered Cost of Ice Cream Bars (in dollars) 0. 16 0. 17 0. 18 0. 20 0. 25 0. 33 0. 35 0. 37 0. 38 0. 40 0. 47 0. 50 0. 63 0. 84 0. 97 0. 99 1. 00 1. 03 1. 07 1. 08 1. 23 2. Find the median. Since there are 27 data values, the median is the 14 th value. median = Q 2 = 0. 50 3. Find Q 1. There are 13 values below the median position. Q 1 is the median of these values. It is the 7 th value. First quartile = Q 1 = 0. 33 4. Find Q 3. There also 13 values about the median. Q 3 is the median of these values. It is the 7 th value from the right end. Third quartile = Q 3 = 1. 00

B. Find the interquartile range IQR = Q 3 – Q 1 = 1. 00 – 0. 33 = 0. 67 This means that the middle half of the data has a cost spread of $0. 67.

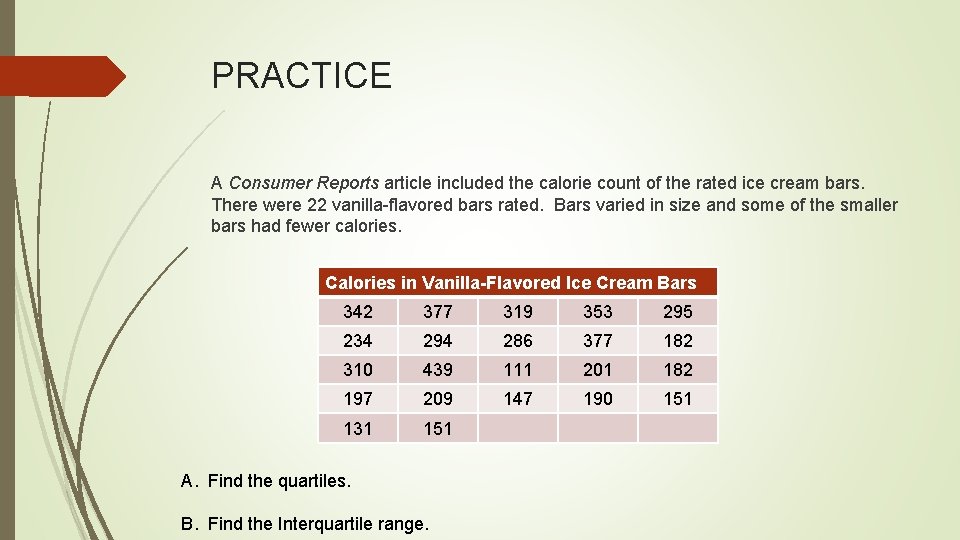
PRACTICE A Consumer Reports article included the calorie count of the rated ice cream bars. There were 22 vanilla-flavored bars rated. Bars varied in size and some of the smaller bars had fewer calories. Calories in Vanilla-Flavored Ice Cream Bars 342 377 319 353 295 234 294 286 377 182 310 439 111 201 182 197 209 147 190 151 131 151 A. Find the quartiles. B. Find the Interquartile range.

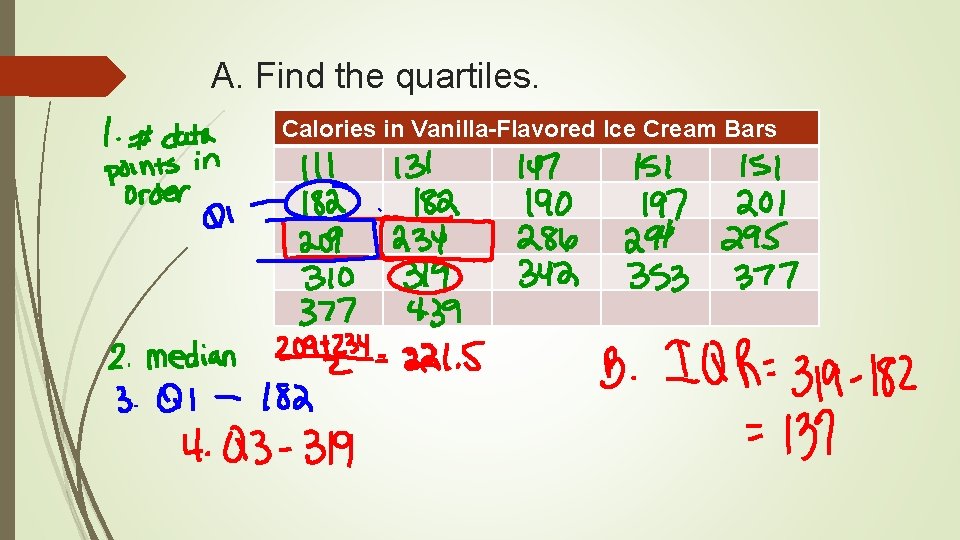
A. Find the quartiles. Calories in Vanilla-Flavored Ice Cream Bars

B. Find the interquartile range

Five-Number Summary 1. 2. We use the 5 -number summary 3. to create a 4. 5. _____________

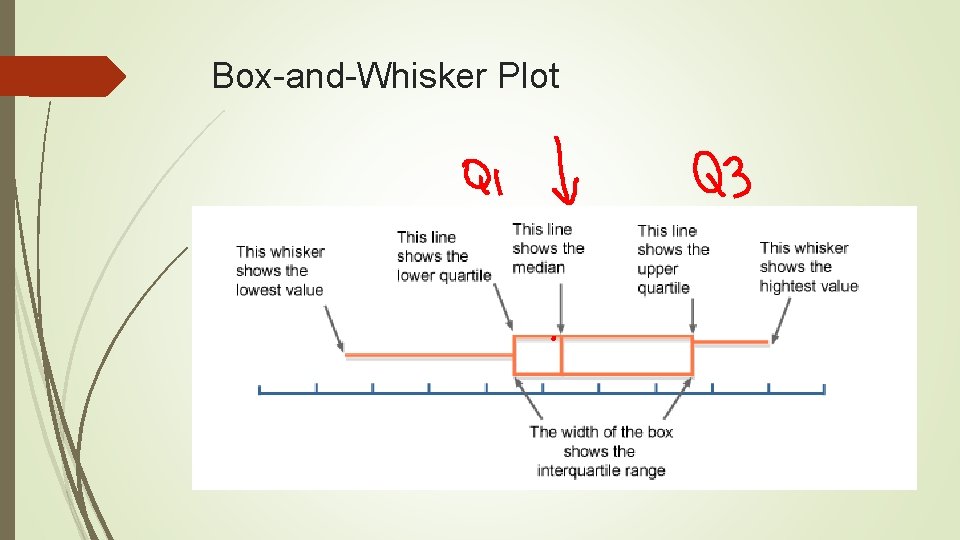
Box-and-Whisker Plot

How to make a box-and-whisker plot 1. Draw a scale to include the lowest and highest data values. 2. Above the scale, draw a box from __________. 3. Include a ____________ through the box at the _________. 4. Draw horizontal lines, called ___________, from Q 1 to the lowest value and from Q 3 to the highest value.

Example Using the data from the last practice problem (calories in ice cream bars), make a boxand-whisker plot. Use the plot to make observations about the distribution of calories. Five-number summary from practice problem: Low value = 111; Q 1 = 182; median = 221. 5; Q 3 = 319; high value = 439

Practice: #5 on pg 109 Homework: A#3. 3 Page 110 #s 6 – 8 Due: ___Thursday, Nov 7_____