Section 3 2 Empirical Rule Chebyshevs Theorem 3

Section 3. 2 Empirical Rule Chebyshev’s Theorem

3 ways to develop a sense for values of standard deviation Range rule of thumb Studied yesterday Empirical (or 68 -95 -99. 7) Rule for Data w/ a Bell-Shaped Distribution Chebyshev’s Theorem

Empirical Rule a. k. a 68 -95 -99. 7 Rule Applies ONLY to Bell-Shaped Distributions!!! The rule states that for data sets having a distribution that is approximately bell-shaped, the following properties apply: o About 68% of all values fall within 1 standard deviation of the mean. o About 95% of all values fall within 2 standard deviations of the mean. o About 99. 7% of all values fall within 3 standard deviations of the mean.

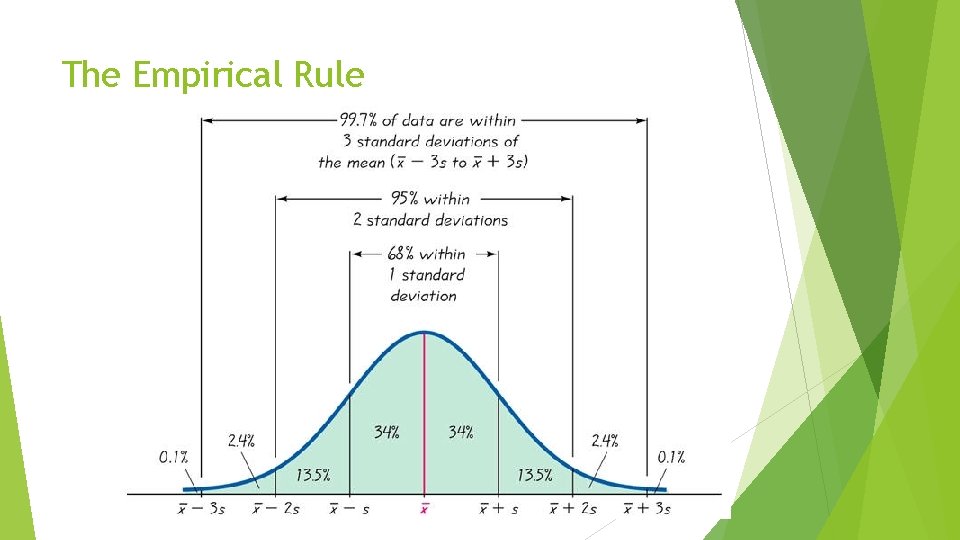
The Empirical Rule

Empirical Rule Example Heights of Men The heights of men have a bell-shaped distribution with a mean of 69. 0 in. and a standard deviation of 2. 8 in. (based on data from the National Health Survey. ) What percentage of men have heights between 60. 6 in. and 77. 4 in. ?

What does “within 3 standard deviations of the mean” mean? ? ? Within 1 standard deviation of the mean - s) and ( + s) Within 2 standard deviations of the mean Between ( - 2 s) and ( + 2 s) Within 3 standard deviations of the mean Between ( - 3 s) and ( + 3 s)

Chebyshev’s Theorem Applies to ANY Data set!!!

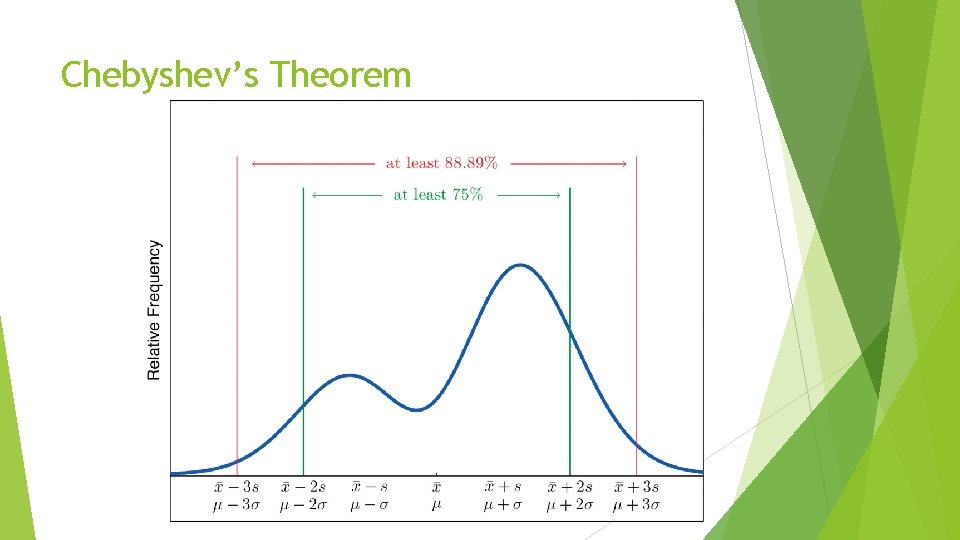
Chebyshev’s Theorem

Chebyshev’s Theorem Example Heights of Men Heights of men have a mean of 69. 0 in. and a standard deviation of 2. 8 in. What can we conclude from Chebyshev’s Theorem?

Chebyshev’s Interval Example The East Coast Independent News periodically runs ads in its own classified section offering a month’s free subscription to those who respond. In this way, management can get a sense about the number of subscribers who read the classified section each day. Over a period of 2 years, careful records have been kept. The mean number of responses per ad is 525 with a standard deviation of s = 30. Determine a Chebyshev Interval about the mean in which at least 89% of the data fall.

Standard Deviation…what do we know? Standard deviation is a measure of variation among scores. Given sample data, you should be able to compute the value of the standard deviation by hand or with a calculator. You should be able to interpret the values of the standard deviations that you compute. You should recognize that for typical data sets, it is unusual for a score to differ from the mean by more than 2 or 3 standard deviations.