Section 3 1 Understanding Linear Trends and Relationships

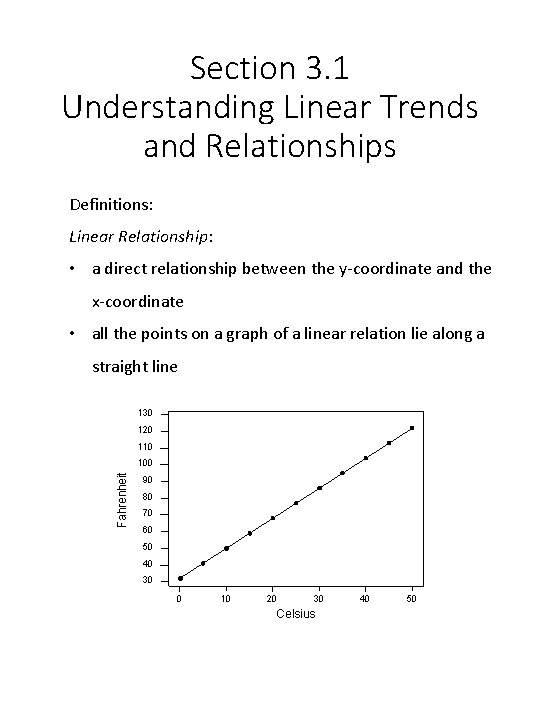
Section 3. 1 Understanding Linear Trends and Relationships Definitions: Linear Relationship: • a direct relationship between the y-coordinate and the x-coordinate • all the points on a graph of a linear relation lie along a straight line

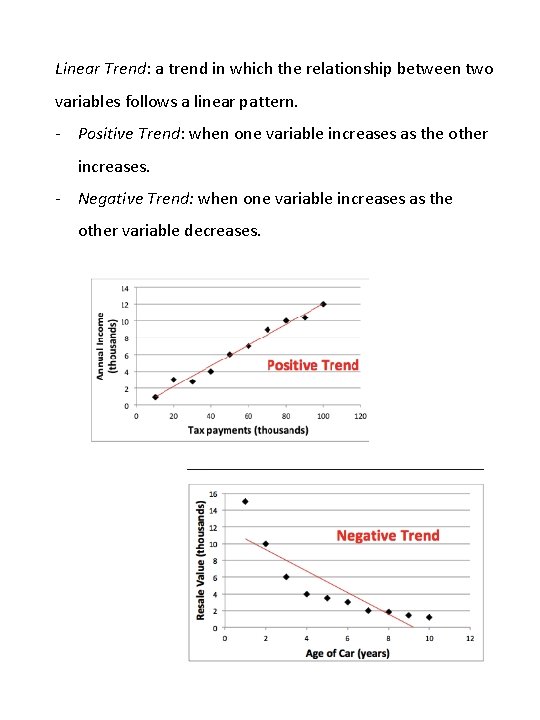
Linear Trend: a trend in which the relationship between two variables follows a linear pattern. - Positive Trend: when one variable increases as the other increases. - Negative Trend: when one variable increases as the other variable decreases.

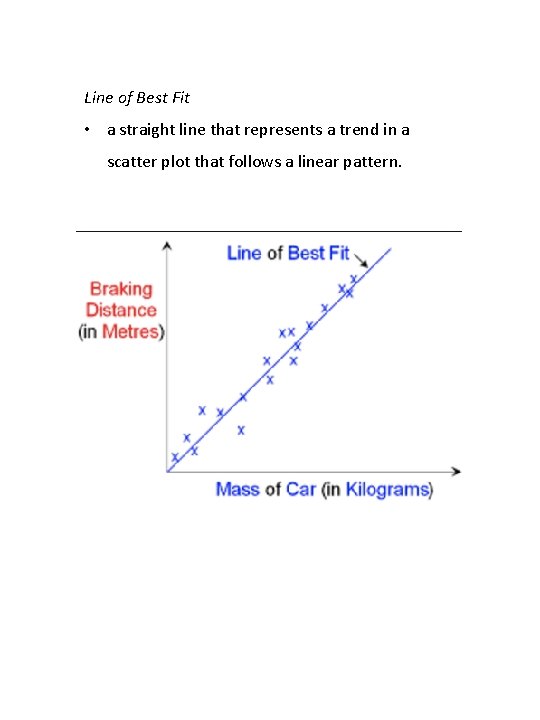
Line of Best Fit • a straight line that represents a trend in a scatter plot that follows a linear pattern.

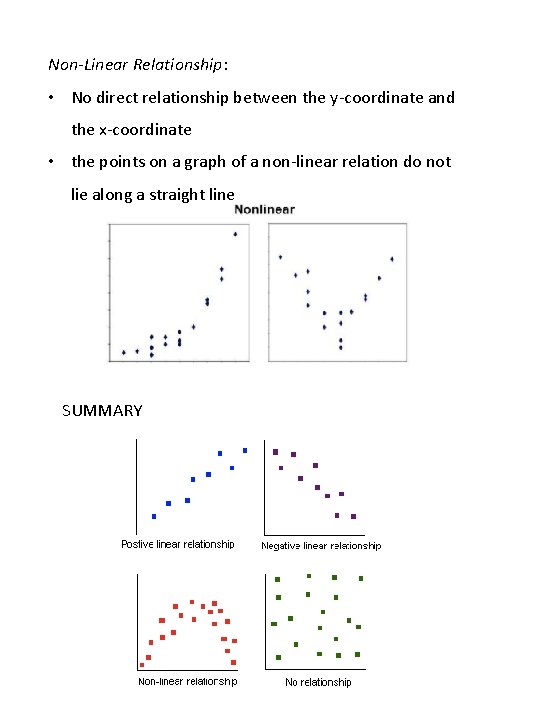
Non-Linear Relationship: • No direct relationship between the y-coordinate and the x-coordinate • the points on a graph of a non-linear relation do not lie along a straight line SUMMARY

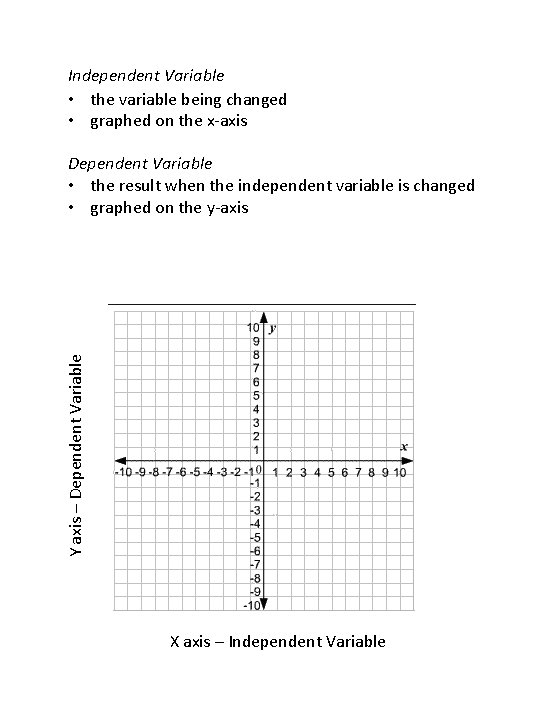
Independent Variable • the variable being changed • graphed on the x-axis Y axis – Dependent Variable • the result when the independent variable is changed • graphed on the y-axis X axis – Independent Variable

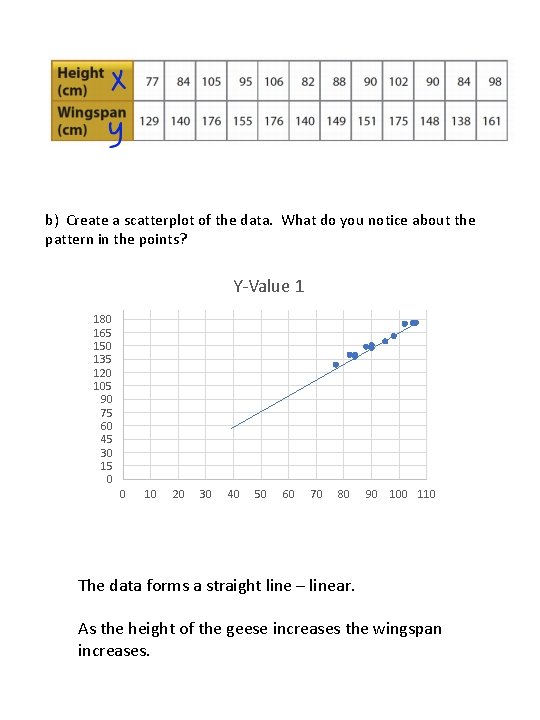
Problem #1 To observe growth or behavior patterns, scientists measure and tag birds and other animals. Mario measures the height and wingspan of 12 geese. He wonders if there is a trend in the relationship between the two variables that will allow him to make a reasonable prediction of the wingspan when he knows the height. a) Describe how to set up the axes of a graph to display the data. - the top row is graphed on the x-axis (independent variable) - the bottom row is graphed on the y-axis (dependent variable)

b) Create a scatterplot of the data. What do you notice about the pattern in the points? Y-Value 1 180 165 150 135 120 105 90 75 60 45 30 15 0 0 10 20 30 40 50 60 70 80 90 100 110 The data forms a straight line – linear. As the height of the geese increases the wingspan increases.

c) Describe the trend in the relationship between the two variables. Is it positive or negative, or is there no trend? - positive trend d) Draw the line of best fit. Describe how well the line represents the trend in the relationship between the variables. - Most of the points are very close to the line of best fit and this shows a strong relationship between the independent and dependent variables. e) Predict the wingspan of a goose that is 100 cm tall. - 165 to 170 cm

Section 3. 1 Comparing Linear and Non-Linear Relationships REMEMBER • A linear relationship is a direct relationship between the y-coordinate and the x-coordinate. All the points on a graph of a linear relation lie along a straight line. • This means the independent and dependent values change at a constant rate. Calculating Rate of Change Distance (km) Cost ($) 0 60 100 80 +100 200 100 +100 300 120 +100 400 140 +20 Independent Variable +100 Dependent Variable +20

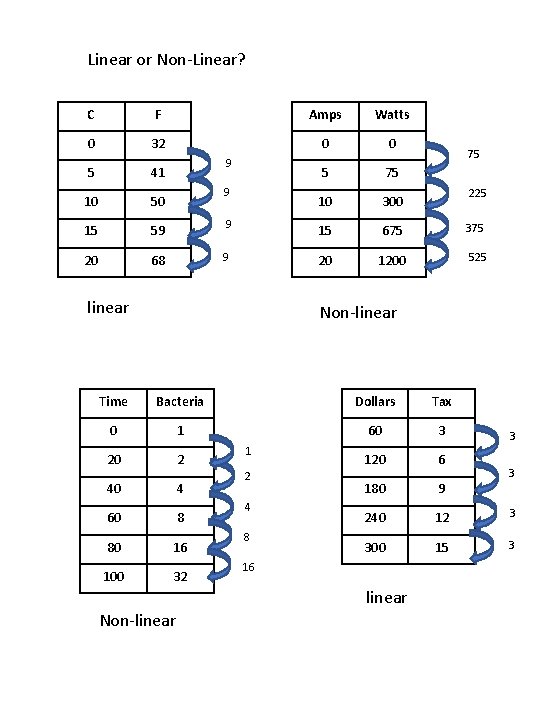
Linear or Non-Linear? C F Amps Watts 0 32 0 0 5 75 10 300 9 75 5 41 10 50 15 59 9 15 675 375 20 68 9 20 1200 525 9 linear 225 Non-linear Time Bacteria Dollars Tax 0 1 60 3 120 6 180 9 240 12 3 300 15 3 20 2 40 4 60 8 80 16 100 32 1 2 4 8 16 linear Non-linear 3 3