Section 3 1 Lines and Angles Perpendicular Lines
- Slides: 23
Section 3. 1 Lines and Angles
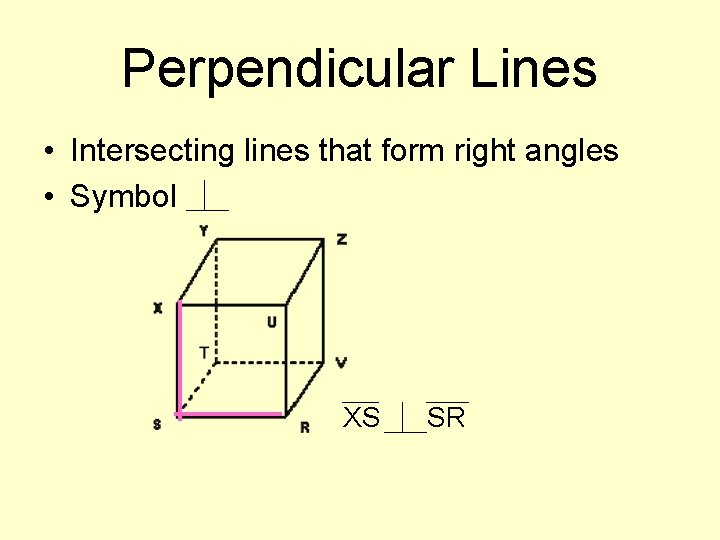
Perpendicular Lines • Intersecting lines that form right angles • Symbol XS SR
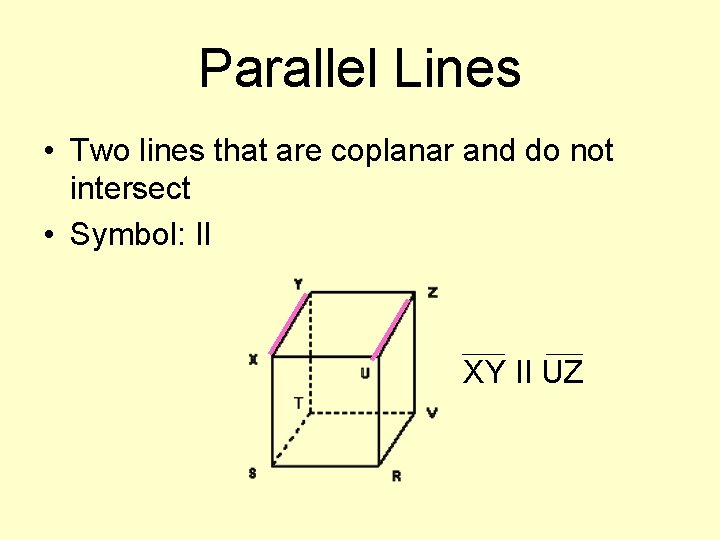
Parallel Lines • Two lines that are coplanar and do not intersect • Symbol: II XY II UZ
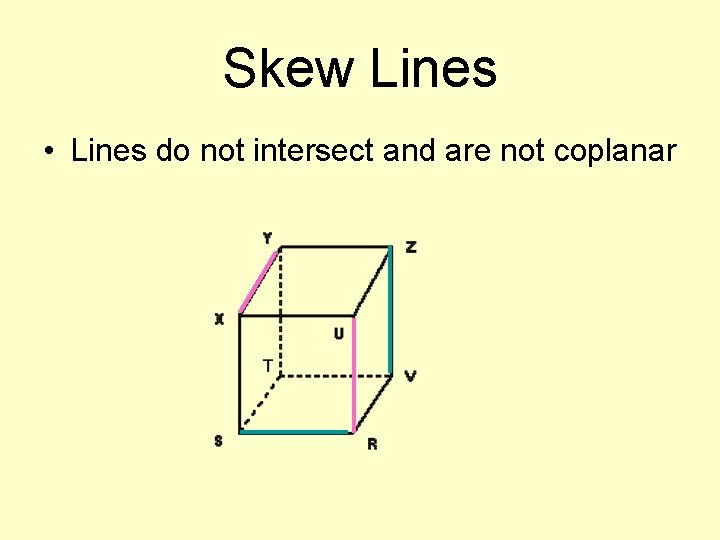
Skew Lines • Lines do not intersect and are not coplanar
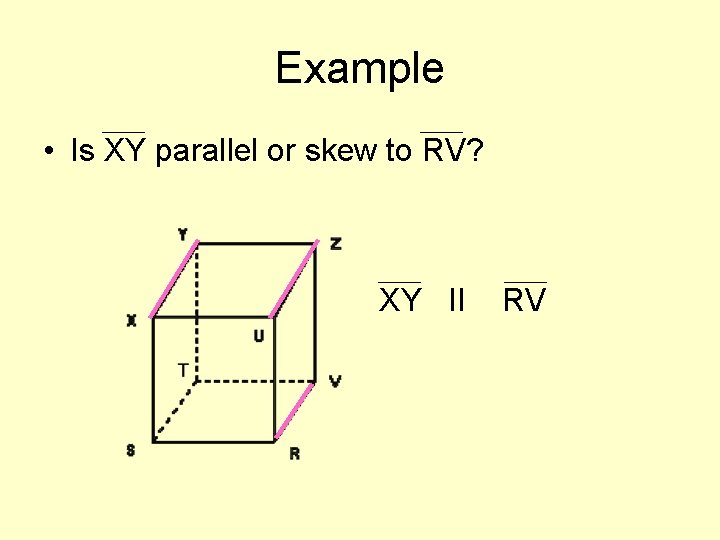
Example • Is XY parallel or skew to RV? XY II RV
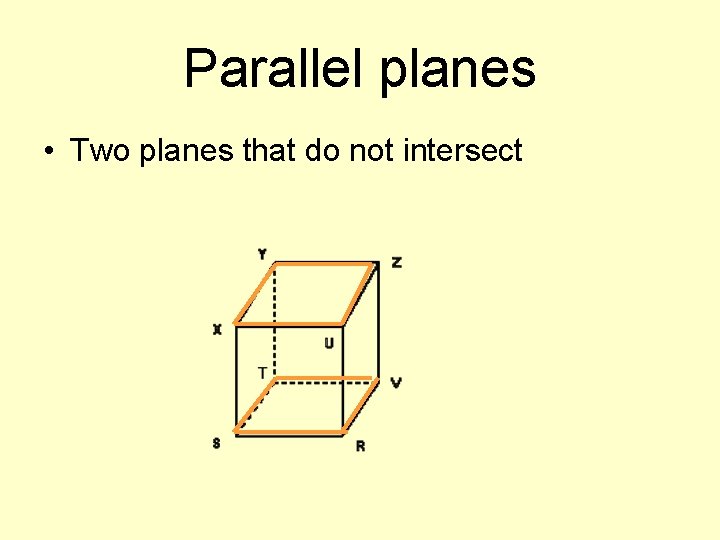
Parallel planes • Two planes that do not intersect
Parallel Postulate • If there is a line and a point not on the line, then there is exactly one line through the point parallel to the given line.
Perpendicular Postulate • If there is a line and a point not on the line, then there is exactly one line through the point perpendicular to the given line.
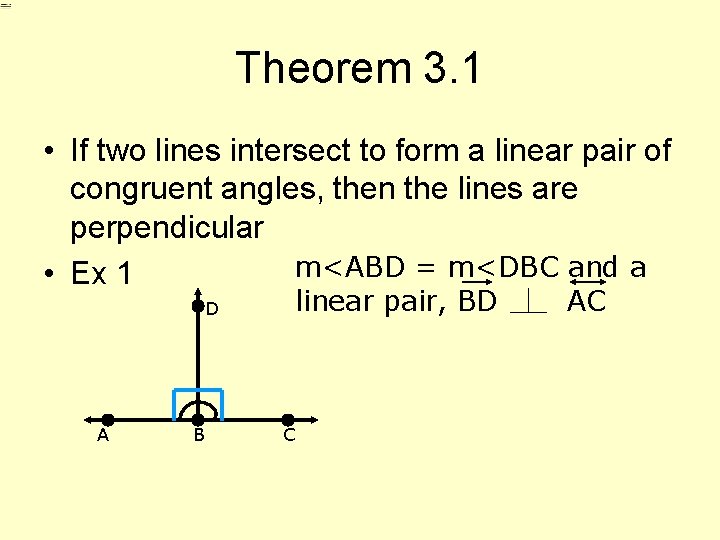
Theorem 3. 1 • If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular m<ABD = m<DBC and a • Ex 1 D A B linear pair, BD C AC
Theorem 3. 2 • If two sides of two adjacent acute angles are perpendicular, then the angles are complementary. • Ex. 2 F J <FGJ is complementary to <JGH G H
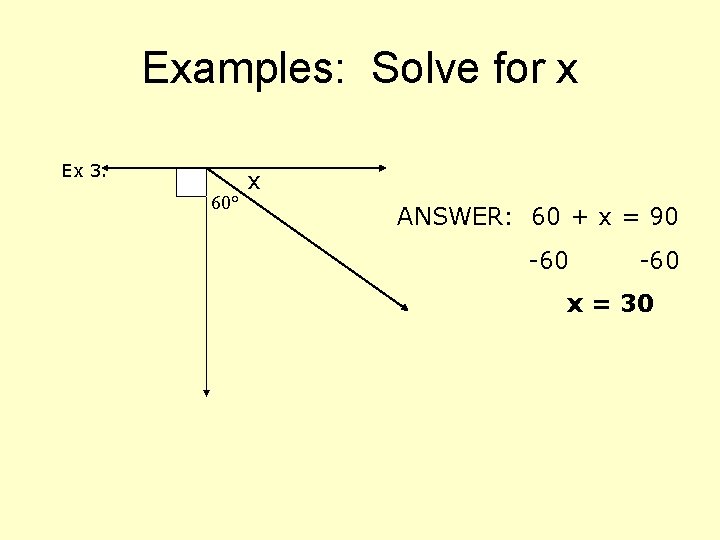
Examples: Solve for x Ex 3. 60° x ANSWER: 60 + x = 90 -60 x = 30
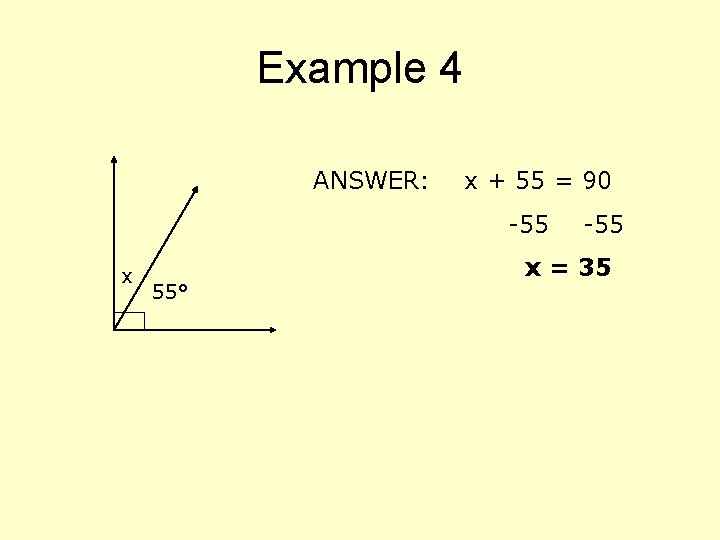
Example 4 ANSWER: x + 55 = 90 -55 x 55° -55 x = 35
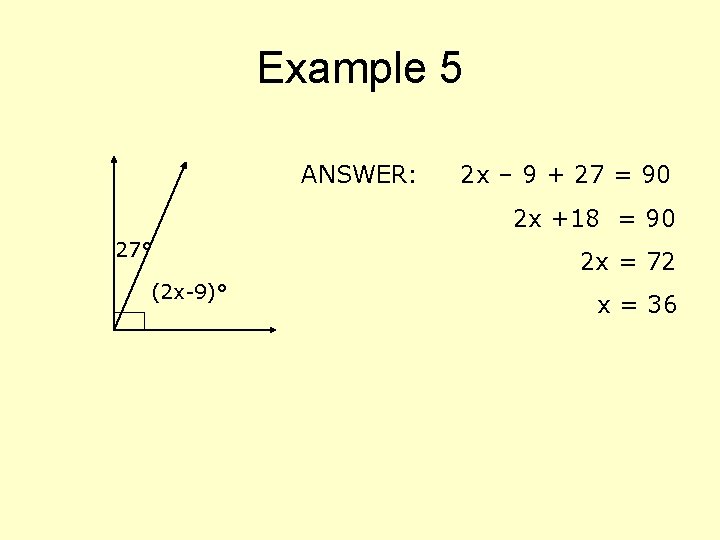
Example 5 ANSWER: 2 x – 9 + 27 = 90 2 x +18 = 90 27° (2 x-9)° 2 x = 72 x = 36
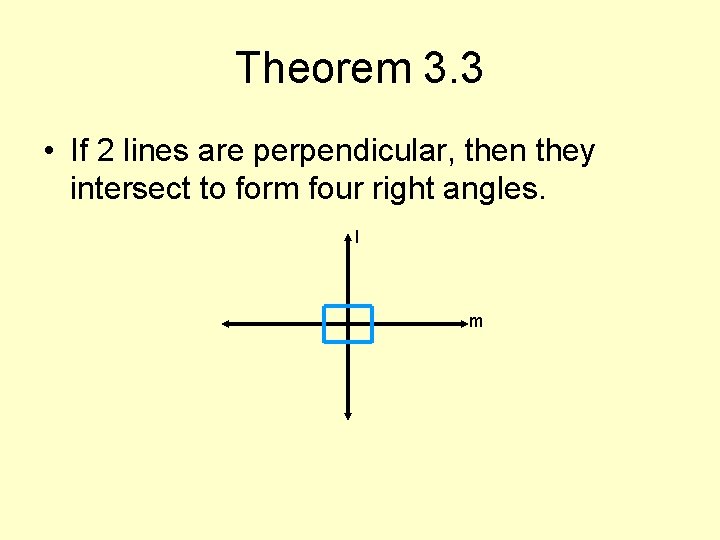
Theorem 3. 3 • If 2 lines are perpendicular, then they intersect to form four right angles. l m
Complete Try it! Problems #1 -8
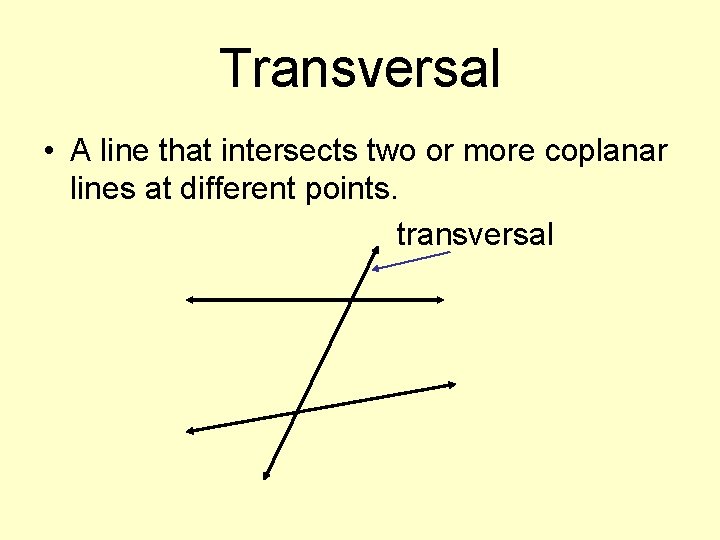
Transversal • A line that intersects two or more coplanar lines at different points. transversal
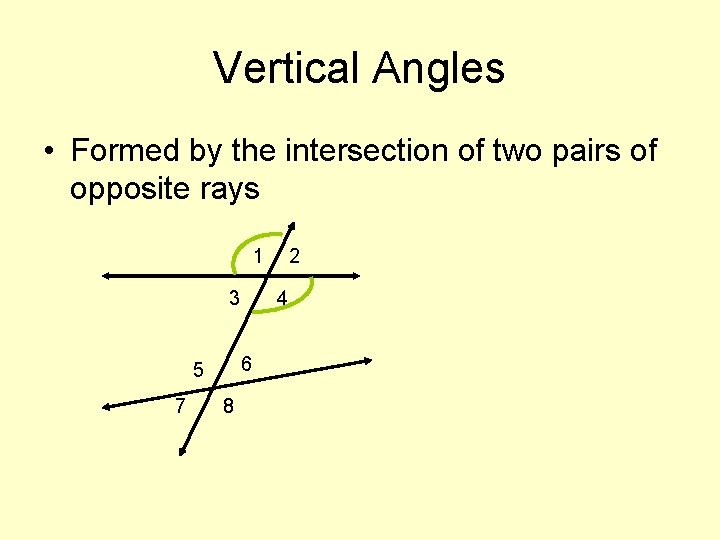
Vertical Angles • Formed by the intersection of two pairs of opposite rays 1 3 7 4 6 5 8 2
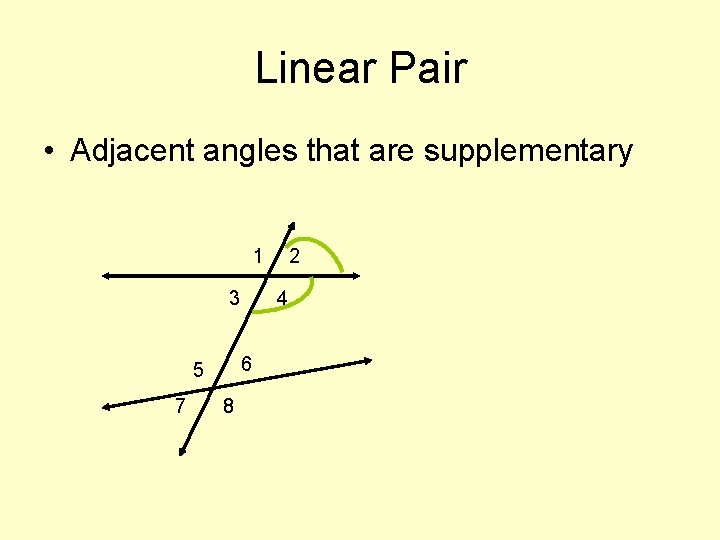
Linear Pair • Adjacent angles that are supplementary 1 3 7 4 6 5 8 2
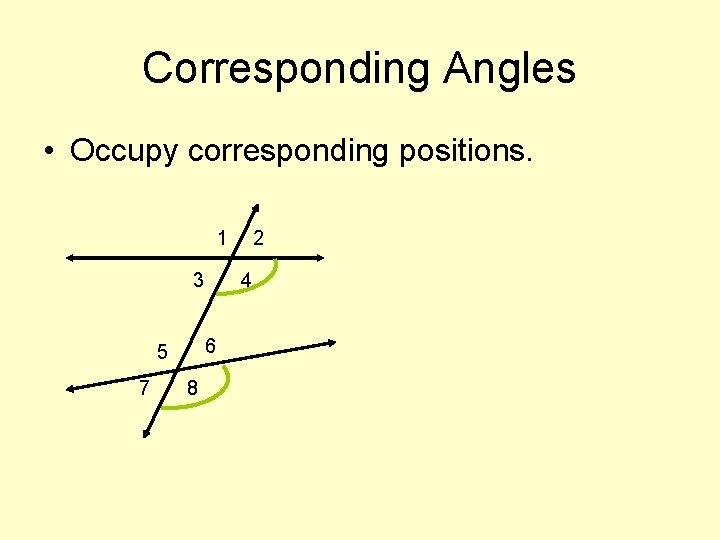
Corresponding Angles • Occupy corresponding positions. 1 3 7 4 6 5 8 2
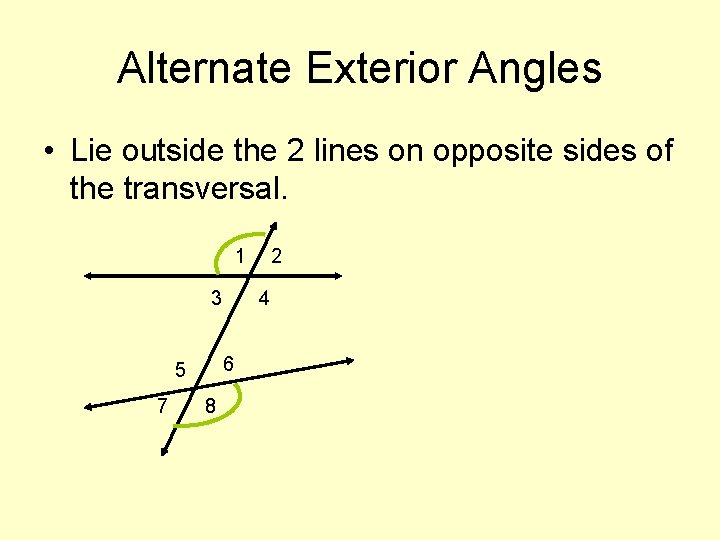
Alternate Exterior Angles • Lie outside the 2 lines on opposite sides of the transversal. 1 3 7 4 6 5 8 2
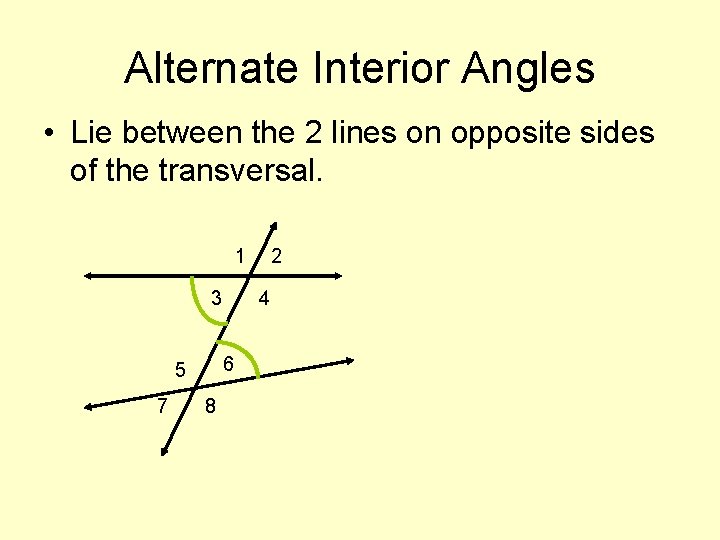
Alternate Interior Angles • Lie between the 2 lines on opposite sides of the transversal. 1 3 7 4 6 5 8 2
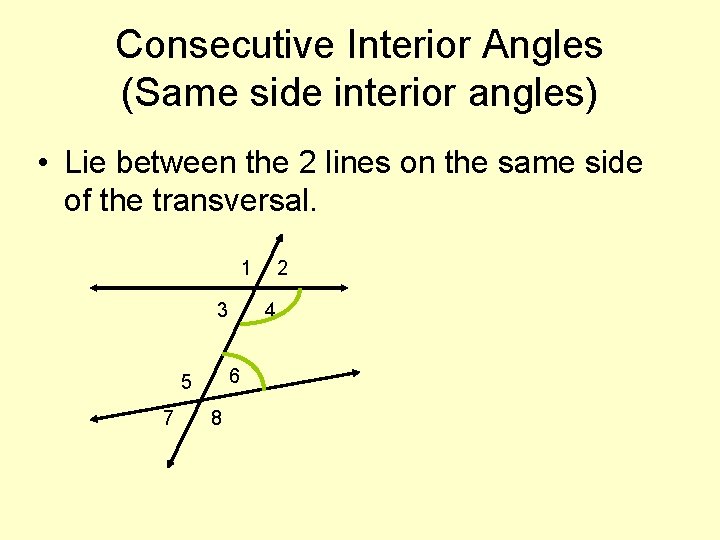
Consecutive Interior Angles (Same side interior angles) • Lie between the 2 lines on the same side of the transversal. 1 3 7 4 6 5 8 2
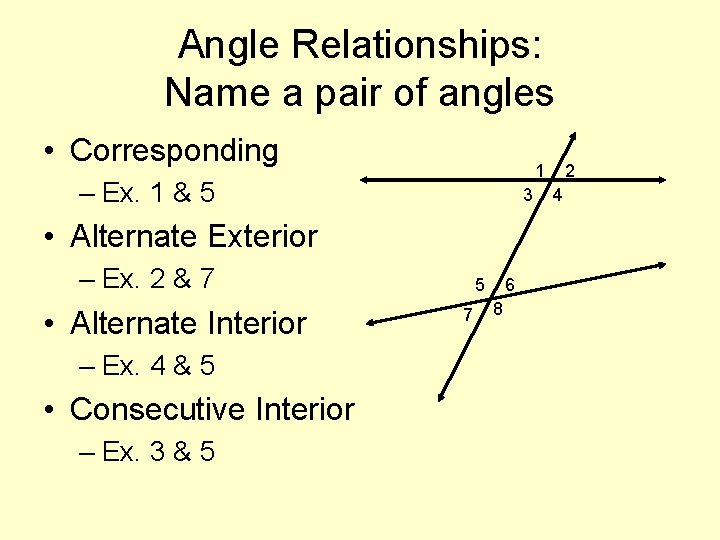
Angle Relationships: Name a pair of angles • Corresponding 1 – Ex. 1 & 5 3 • Alternate Exterior – Ex. 2 & 7 • Alternate Interior – Ex. 4 & 5 • Consecutive Interior – Ex. 3 & 5 5 7 6 8 2 4
Property of vertically opposite angles
What are skew lines in geometry
3-2 properties of parallel lines part 1 answers
Section 3-2 angles and parallel lines
Parallel lines and transversals assignment
Module 15 angles and segments in circles answer key
G.v. black's classification
Answer key unit 3 parallel and perpendicular lines
Proofs involving parallel lines
Opposite reciprocal slope
Parallel and perpendicular slopes
Parallel and perpendicular lines slope intercept form
Slopes of parallel and perpendicular lines assignment
Lesson 8 parallel and perpendicular lines
Chapter 3 review parallel and perpendicular lines
Write equations of parallel and perpendicular lines
Chapter 3 review parallel and perpendicular lines
Chapter 3 parallel and perpendicular lines
Chapter 3 parallel and perpendicular lines answers
Lesson 2-4 slopes of parallel and perpendicular lines
E.6 equations of parallel and perpendicular lines
4-4 parallel and perpendicular lines
Perpendicular
3 sets of parallel lines
