Section 3 1 Exploring Symmetry Objectives Identify the

Section 3. 1 Exploring Symmetry

Objectives • Identify the image and pre-image points and the axis of symmetry of a set of ordered pairs. • Determine the relationship of coordinates of points reflected over the y-axis, the x-axis, the origin, and the line y = x.

y-axis symmetry x-axis symmetry origin symmetry

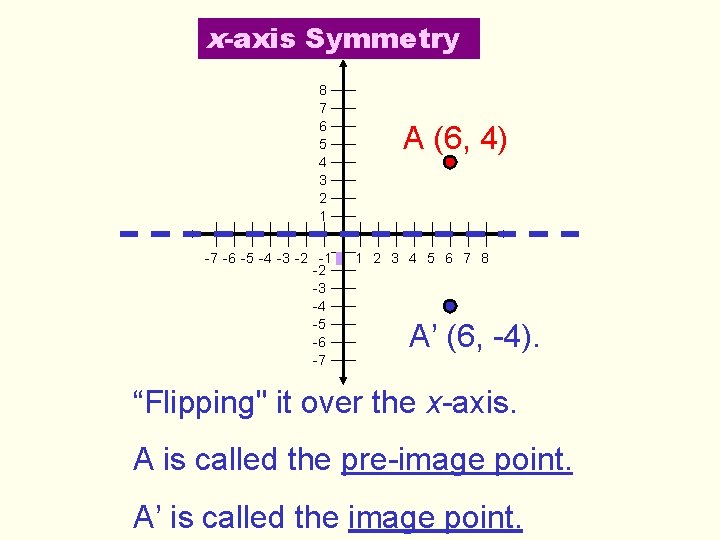
x-axis Symmetry 8 7 6 5 4 3 2 1 A (6, 4) -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 -2 -3 -4 -5 -6 -7 A’ (6, -4). “Flipping" it over the x-axis. A is called the pre-image point. A’ is called the image point.

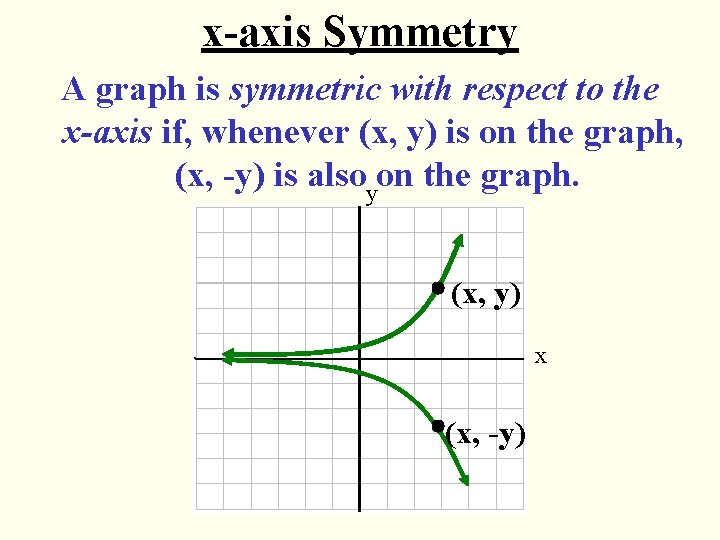
x-axis Symmetry A graph is symmetric with respect to the x-axis if, whenever (x, y) is on the graph, (x, -y) is alsoyon the graph. (x, y) x (x, -y)

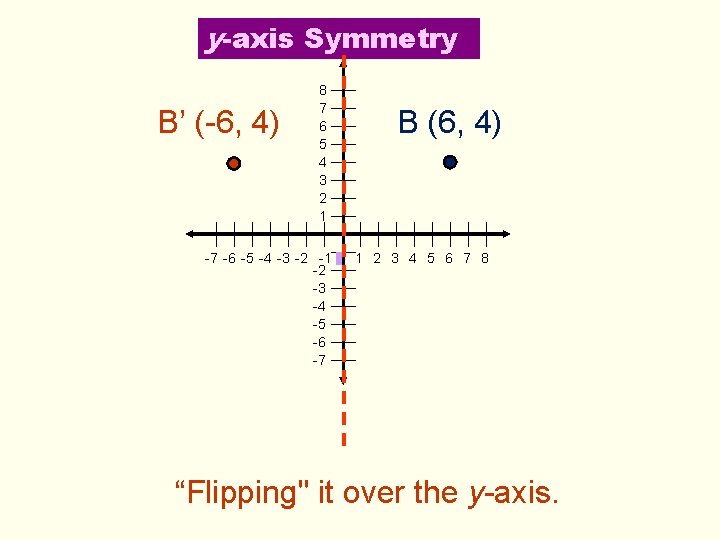
y-axis Symmetry B’ (-6, 4) 8 7 6 5 4 3 2 1 B (6, 4) -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 -2 -3 -4 -5 -6 -7 “Flipping" it over the y-axis.

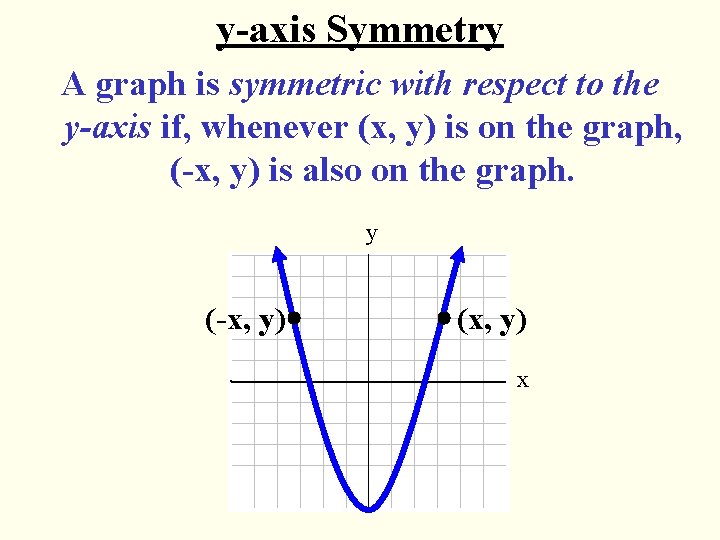
y-axis Symmetry A graph is symmetric with respect to the y-axis if, whenever (x, y) is on the graph, (-x, y) is also on the graph. y (-x, y) (x, y) x

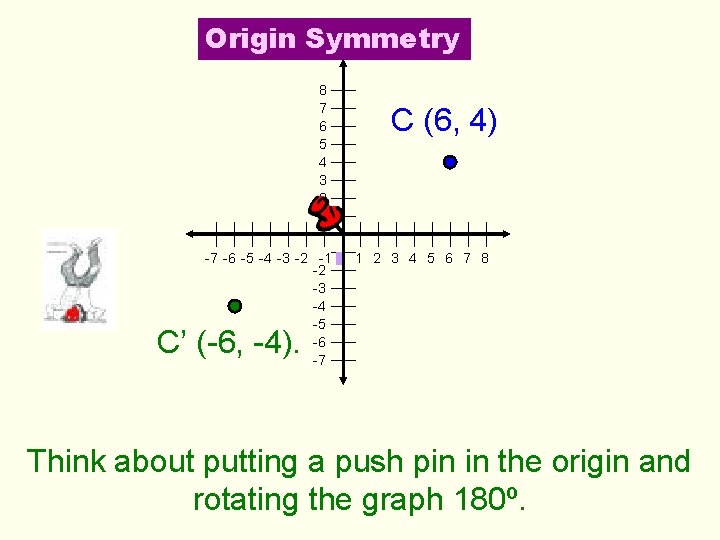
Origin Symmetry 8 7 6 5 4 3 2 1 C (6, 4) -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 -2 -3 -4 -5 -6 -7 C’ (-6, -4). Think about putting a push pin in the origin and rotating the graph 180º.

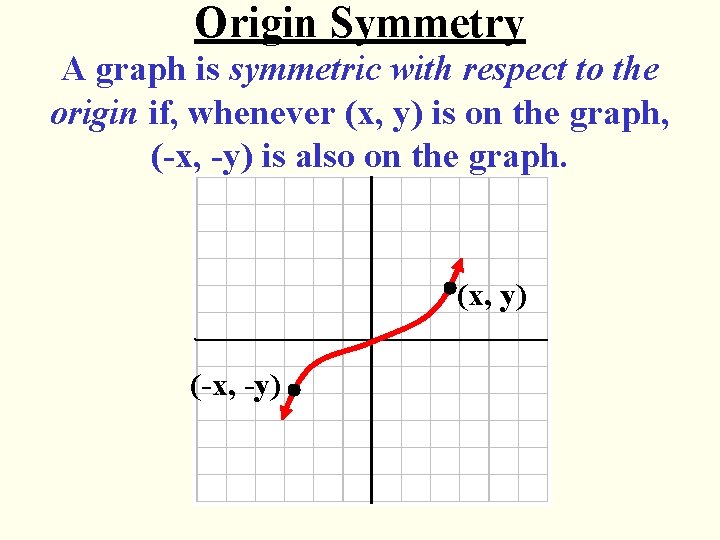
Origin Symmetry A graph is symmetric with respect to the origin if, whenever (x, y) is on the graph, (-x, -y) is also on the graph. (x, y) (-x, -y)

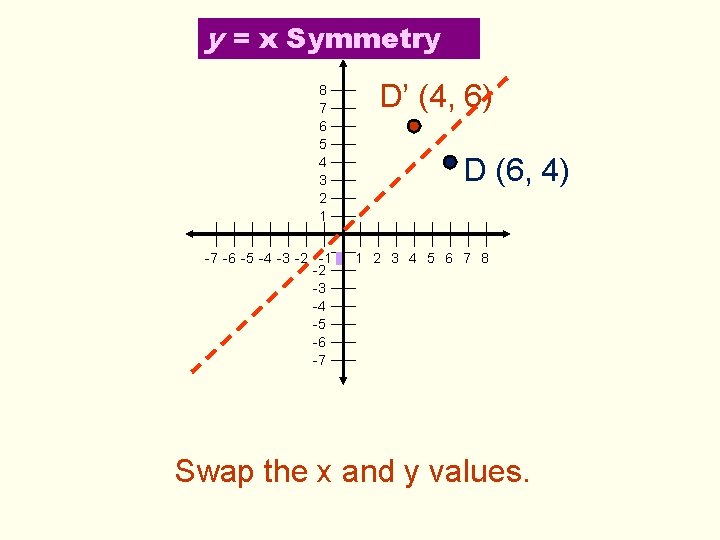
y = x Symmetry 8 7 6 5 4 3 2 1 D’ (4, 6) D (6, 4) -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 -2 -3 -4 -5 -6 -7 Swap the x and y values.

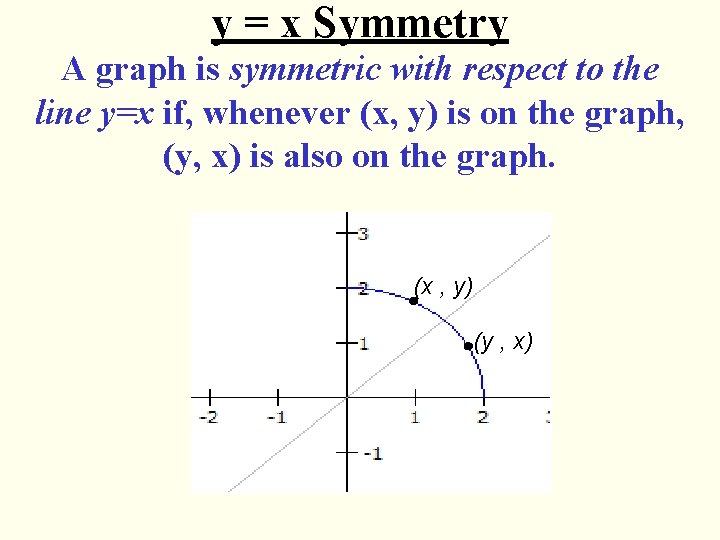
y = x Symmetry A graph is symmetric with respect to the line y=x if, whenever (x, y) is on the graph, (y, x) is also on the graph. (x , y) (y , x)

Extension: Checking the symmetry of graphs…

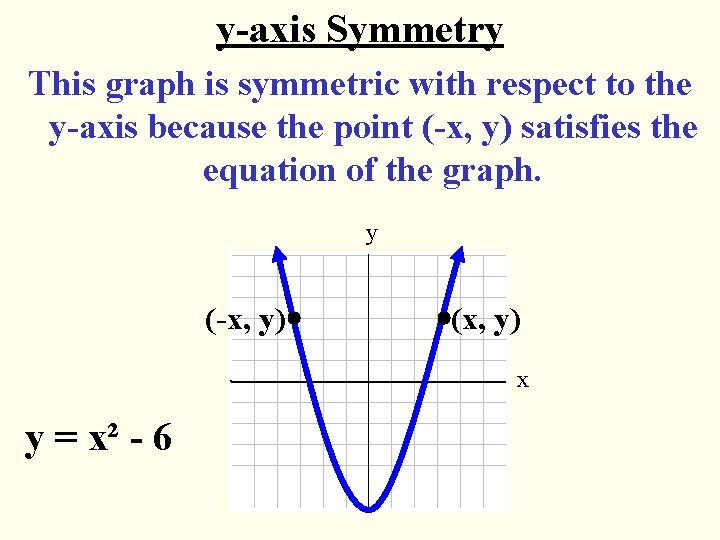
y-axis Symmetry This graph is symmetric with respect to the y-axis because the point (-x, y) satisfies the equation of the graph. y (-x, y) (x, y) x y = x² - 6

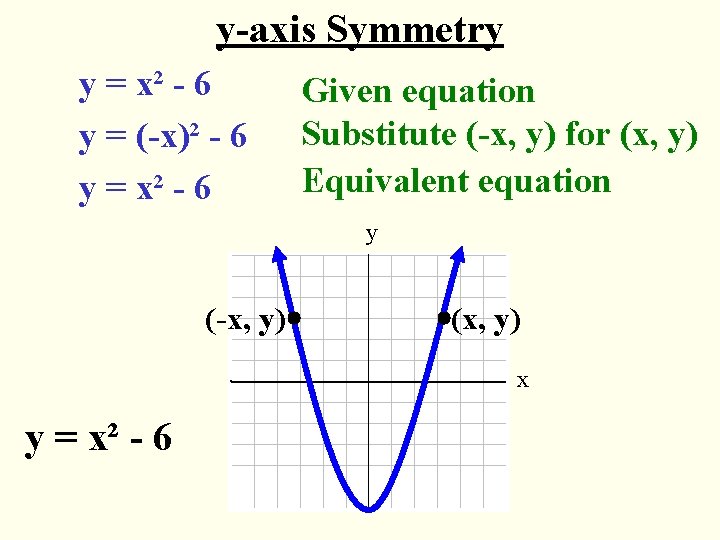
y-axis Symmetry y = x² - 6 y = (-x)² - 6 y = x² - 6 Given equation Substitute (-x, y) for (x, y) Equivalent equation y (-x, y) (x, y) x y = x² - 6

Tests for Symmetry Given an equation, test whether the graph has symmetry by doing the following: Replace y with –y. After simplifying, you x-axis get the original equation back y-axis Replace x with –x. After simplifying, you get the original equation back Replace x with –x and y with -y. After Origin simplifying, you get the original equation back. Swap the x and the y. After simplifying, y = x you get the original equation back

Test for symmetry: So graph has x -axis symmetry Since a negative squared is positive x-axis Replace y by –y. After simplifying, you get the original equation back.

Test for symmetry: NO! Not the same! DOES NOT have y-axis symmetry ? y-axis Replace x by –x. After simplifying, you get the original equation back.

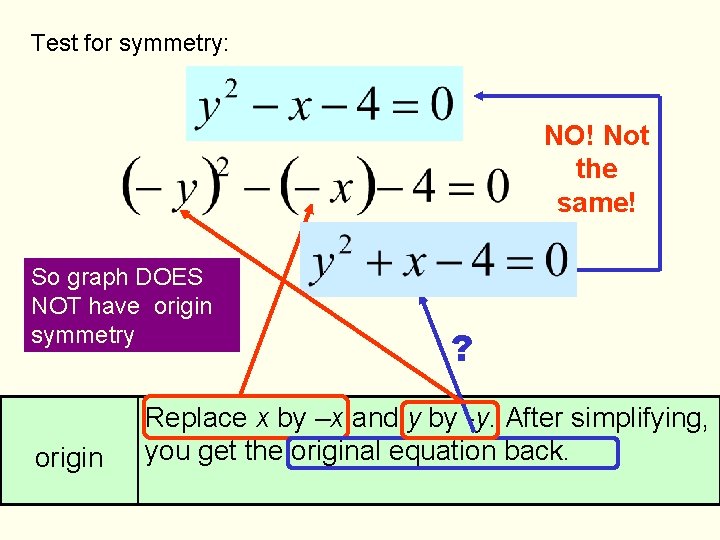
Test for symmetry: NO! Not the same! So graph DOES NOT have origin symmetry origin ? Replace x by –x and y by -y. After simplifying, you get the original equation back.

Test for symmetry: NO! Not the same! So graph DOES NOT have symmetry with respect to y=x ? Swap the x and the y. After simplifying, you get the original equation back.

Classwork: • Section 3. 1 Symmetry Worksheet

Homework: Section 3. 1 Practice and Apply Worksheet