Section 2 Radioactive Decay Unstable nuclei can break

Section 2: Radioactive Decay Unstable nuclei can break apart spontaneously, changing the identity of atoms. K What I Know W What I Want to Find Out L What I Learned

• 12(B) Describe radioactive decay process in terms of balanced nuclear equations. • 2(H) Organize, analyze, evaluate, make inferences, and predict trends from data. • 2(I) Communicate valid conclusions supported by the data through methods such as lab reports, labeled drawings, graphs, journals, summaries, oral reports, and technology–based reports. • 12(A) Describe the characteristics of alpha, beta, and gamma radiation. Copyright © Mc. Graw-Hill Education Radioactive Decay

Essential Questions • Why are certain nuclei radioactive? • How are nuclear equations balanced? • How can you use radioactive decay rates to analyze samples of radioisotopes? Copyright © Mc. Graw-Hill Education Radioactive Decay

Vocabulary Review New • radioactivity • • • Copyright © Mc. Graw-Hill Education transmutation nucleon strong nuclear force band of stability positron emission positron electron capture radioactive decay series half-life radiochemical dating Radioactive Decay

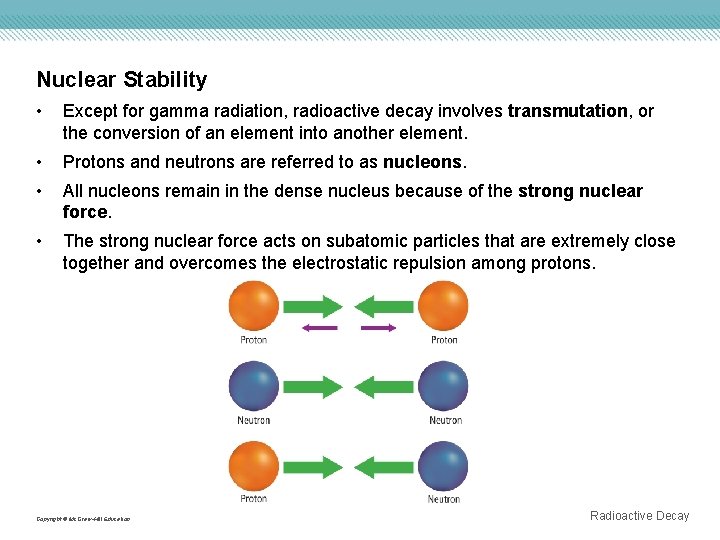
Nuclear Stability • Except for gamma radiation, radioactive decay involves transmutation, or the conversion of an element into another element. • Protons and neutrons are referred to as nucleons. • All nucleons remain in the dense nucleus because of the strong nuclear force. • The strong nuclear force acts on subatomic particles that are extremely close together and overcomes the electrostatic repulsion among protons. Copyright © Mc. Graw-Hill Education Radioactive Decay

Nuclear Stability • As atomic number increases, more and more neutrons are needed to produce a strong nuclear force that is sufficient to balance the electrostatic repulsion between protons. • Neutron to proton ratio increases gradually to about 1. 5: 1. Copyright © Mc. Graw-Hill Education Radioactive Decay

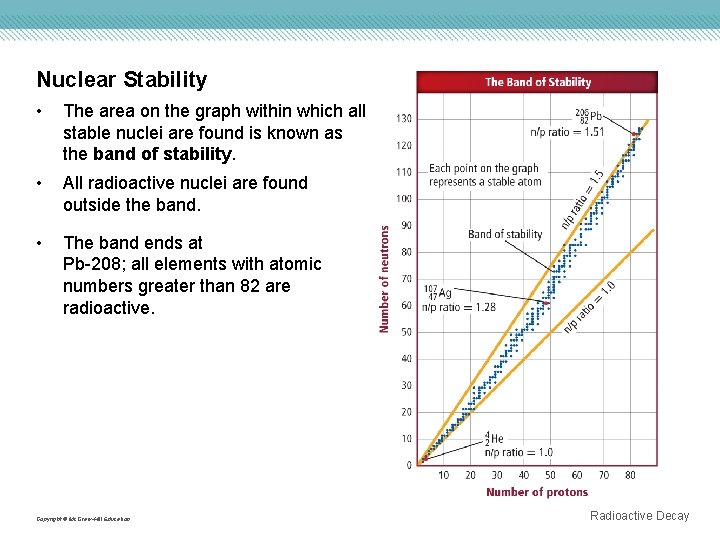
Nuclear Stability • The area on the graph within which all stable nuclei are found is known as the band of stability. • All radioactive nuclei are found outside the band. • The band ends at Pb-208; all elements with atomic numbers greater than 82 are radioactive. Copyright © Mc. Graw-Hill Education Radioactive Decay

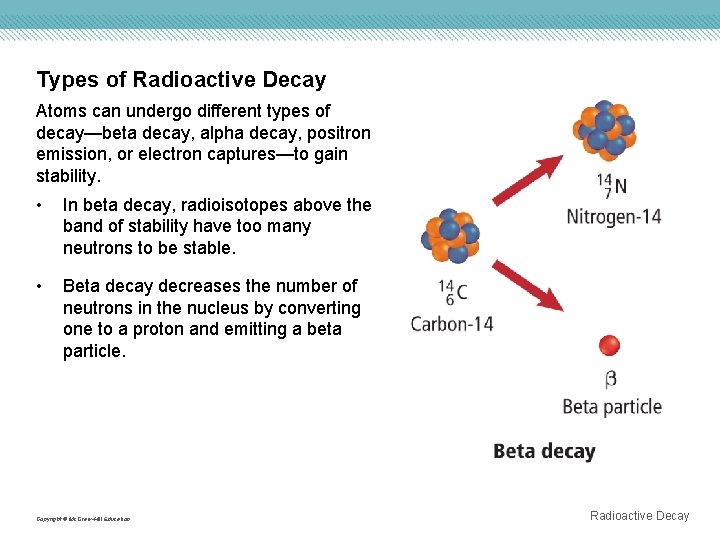
Types of Radioactive Decay Atoms can undergo different types of decay—beta decay, alpha decay, positron emission, or electron captures—to gain stability. • In beta decay, radioisotopes above the band of stability have too many neutrons to be stable. • Beta decay decreases the number of neutrons in the nucleus by converting one to a proton and emitting a beta particle. Copyright © Mc. Graw-Hill Education Radioactive Decay

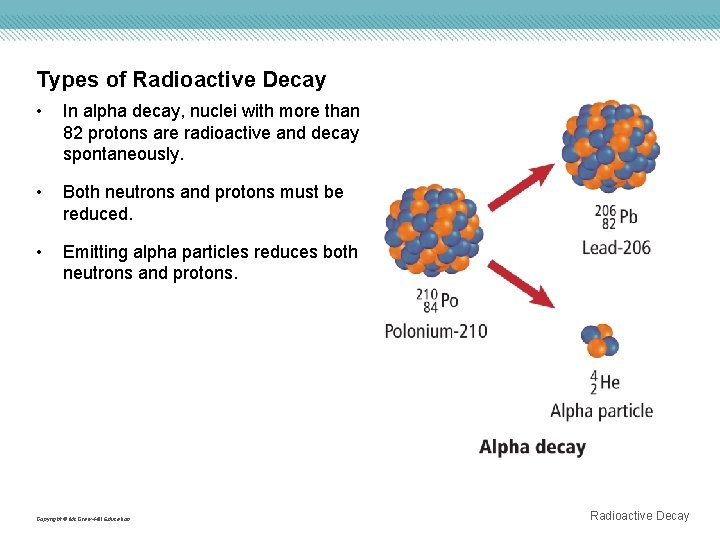
Types of Radioactive Decay • In alpha decay, nuclei with more than 82 protons are radioactive and decay spontaneously. • Both neutrons and protons must be reduced. • Emitting alpha particles reduces both neutrons and protons. Copyright © Mc. Graw-Hill Education Radioactive Decay

Types of Radioactive Decay Nuclei with low neutron to proton ratios have two common decay processes. • A positron is a particle with the same mass as an electron but opposite charge. • Positron emission is a radioactive decay process that involves the emission of a positron from the nucleus. • During positron emission, a proton in the nucleus is converted to a neutron and a positron, and the positron is then emitted. • Electron capture occurs when the nucleus of an atom draws in a surrounding electron and combines with a proton to form a neutron. Copyright © Mc. Graw-Hill Education Radioactive Decay

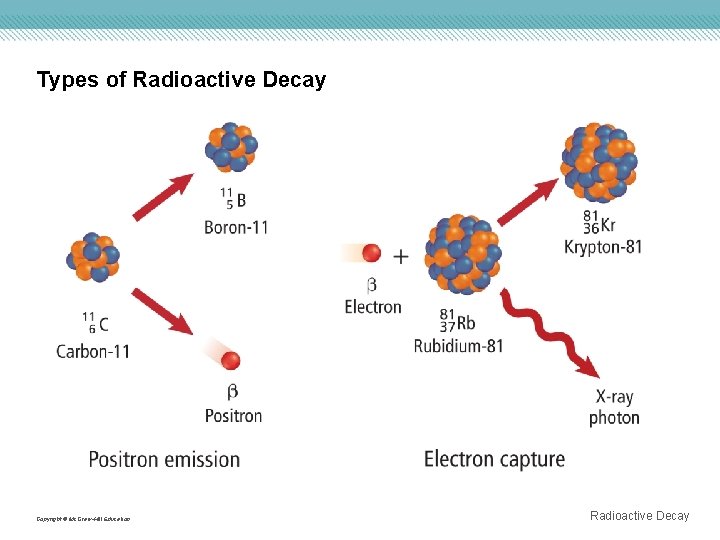
Types of Radioactive Decay Copyright © Mc. Graw-Hill Education Radioactive Decay

Writing and Balancing Nuclear Equations Nuclear reactions are expressed by balanced nuclear equations. • In balanced nuclear equations, mass numbers and charges are conserved. Ex. A plutonium-238 atom undergoes alpha decay, write a balanced equation for this decay. Copyright © Mc. Graw-Hill Education Radioactive Decay

BALANCING A NUCLEAR EQUATION UNKNOWN mass number of the product A = ? atomic number of the product Z = ? reaction product X = ? Response ANALYZE THE PROBLEM You are given that a plutonium atom undergoes alpha decay and forms an unknown product. Plutonium-238 is the initial reactant, while the alpha particle is one of the products of the reaction. KNOWN Copyright © Mc. Graw-Hill Education EVALUATE THE ANSWER The correct formula for an alpha particle is used. The sums of the superscripts and subscripts on each side of the equation are equal. Therefore, the charge and the mass number are conserved. The nuclear equation is balanced. Radioactive Decay

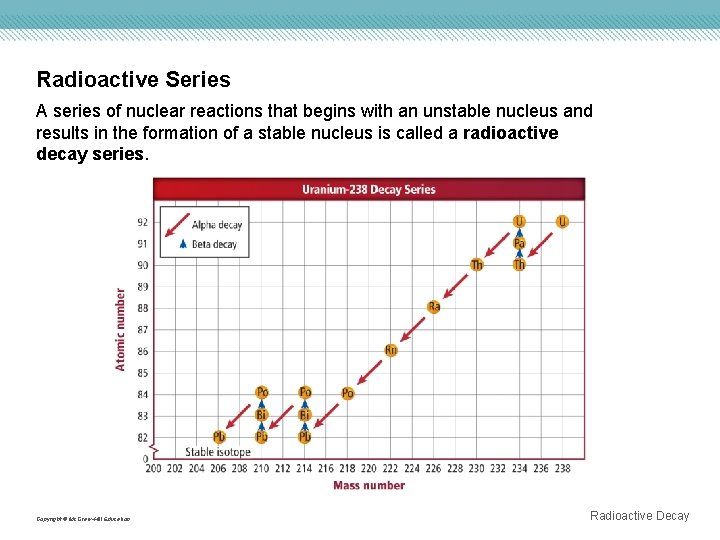
Radioactive Series A series of nuclear reactions that begins with an unstable nucleus and results in the formation of a stable nucleus is called a radioactive decay series. Copyright © Mc. Graw-Hill Education Radioactive Decay

Radioactive Decay Rates A half-life is the time required for one-half of a radioisotope to decay into its products. • Radioactive decay rates are measured in half-lives. N is the remaining amount. N 0 is the initial amount. n is the number of half-lives that have passed. t is the elapsed time and T is the duration of the half-life. Copyright © Mc. Graw-Hill Education Radioactive Decay

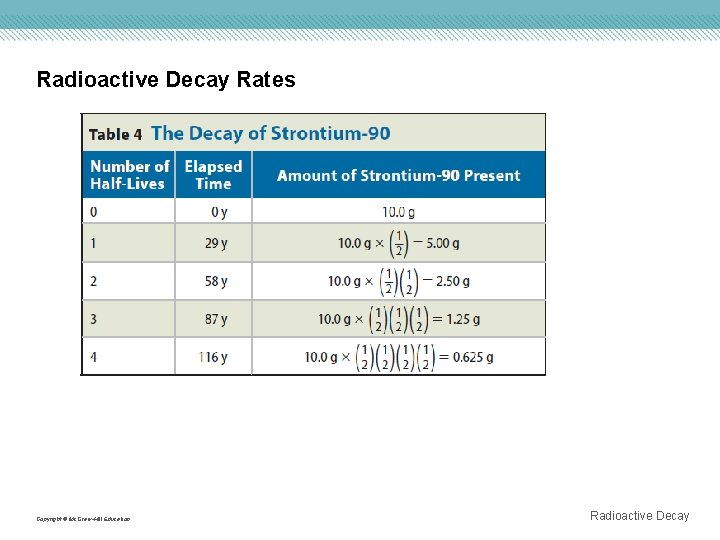
Radioactive Decay Rates Copyright © Mc. Graw-Hill Education Radioactive Decay

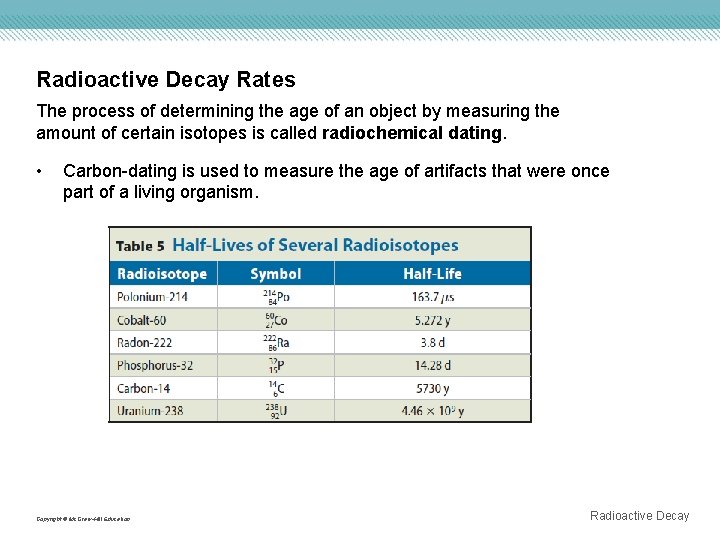
Radioactive Decay Rates The process of determining the age of an object by measuring the amount of certain isotopes is called radiochemical dating. • Carbon-dating is used to measure the age of artifacts that were once part of a living organism. Copyright © Mc. Graw-Hill Education Radioactive Decay

CALCULATING THE AMOUNT OF REMAINING ISOTOPE Use with Example Problem 2. Problem Krypton-85 is used in indicator lights of appliances. The half-life of krypton-85 is 11 y. How much of a 2. 000 -mg sample remains after 33 y? KNOWN Initial amount = 2. 000 mg Elapsed time (t) = 33 y Copyright © Mc. Graw-Hill Education Response ANALYZE THE PROBLEM You are given a known mass of a radioisotope with a known half-life. You must first determine the number of half-lives that passed during the 33 -year period. Then, use the exponential decay equation to calculate the amount of the sample remaining. UNKNOWN Amount remaining = ? mg Half-life (T ) = 11 y Radioactive Decay

CALCULATING THE AMOUNT OF REMAINING ISOTOPE Copyright © Mc. Graw-Hill Education Radioactive Decay

Review Essential Questions • Why are certain nuclei radioactive? • How are nuclear equations balanced? • How can you use radioactive decay rates to analyze samples of radioisotopes? Vocabulary • transmutation • nucleon • strong nuclear force • band of stability Copyright © Mc. Graw-Hill Education • • positron emission positron electron capture radioactive decay series • half-life • radiochemical dating Radioactive Decay