SECTION 2 QUANTUM THEORY AND THE ATOM CHAPTER

SECTION 2: QUANTUM THEORY AND THE ATOM CHAPTER 9: ELECTRONS IN ATOMS AND THE PERIODIC TABLE

Learning Goals • Compare the Bohr and quantum mechanical models of the atom. • Explain the impact of de Broglie’s wave particle duality and the Heisenberg uncertainty principle on the current view of electrons in atoms. • Identify the relationships among a hydrogen atom’s energy levels, sublevels, and atomic orbitals.

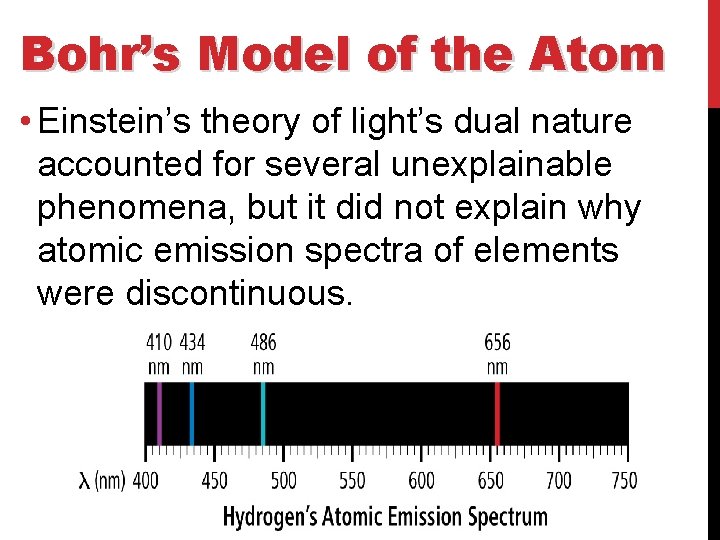
Bohr’s Model of the Atom • Einstein’s theory of light’s dual nature accounted for several unexplainable phenomena, but it did not explain why atomic emission spectra of elements were discontinuous.

Bohr’s Model of the Atom • In 1913, Niels Bohr, a Danish physicist working in Rutherford’s laboratory, proposed a quantum model for the hydrogen atom that seemed to answer this question. • This model correctly predicted the frequency lines in hydrogen’s atomic emission spectrum.

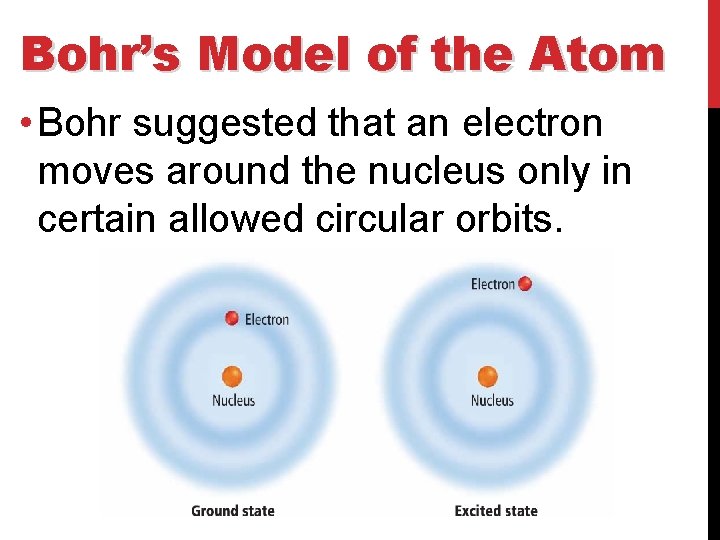
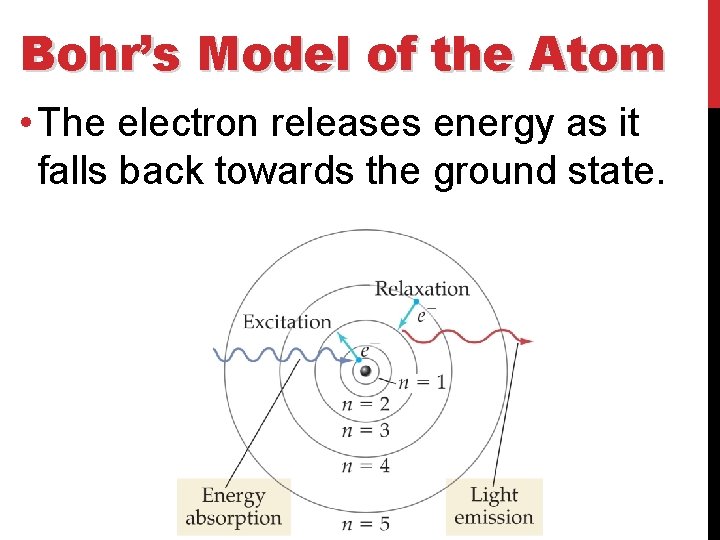
Bohr’s Model of the Atom • The lowest allowable energy state of an atom is called its ground state. • When an atom gains energy, it is in an excited state.

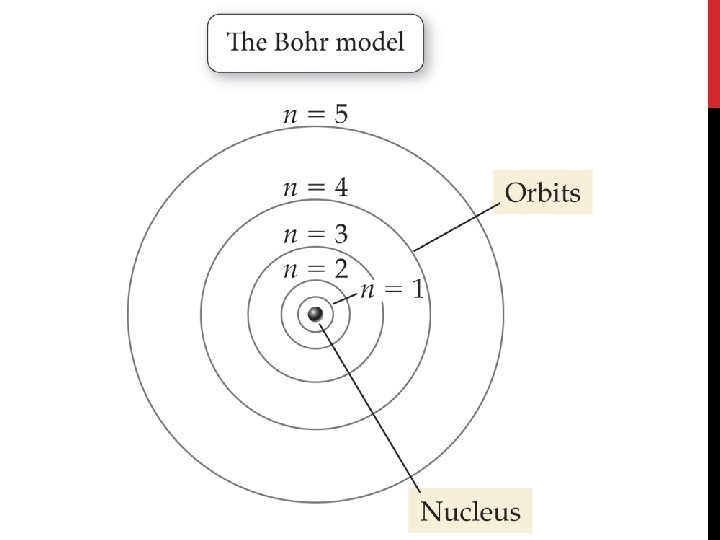
Bohr’s Model of the Atom • Bohr suggested that an electron moves around the nucleus only in certain allowed circular orbits.

Bohr’s Model of the Atom • Each orbit was given a number, called the quantum number. • Bohr orbits are like steps of a ladder, each at a specific distance from the nucleus and each at a specific energy.

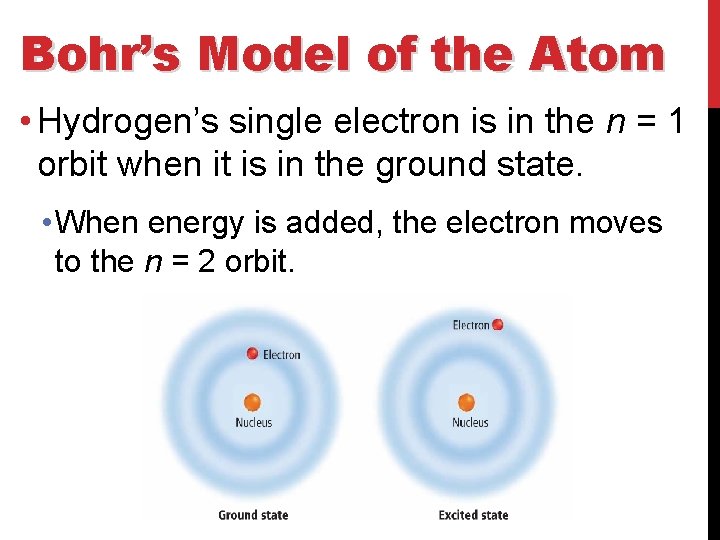
Bohr’s Model of the Atom • Hydrogen’s single electron is in the n = 1 orbit when it is in the ground state. • When energy is added, the electron moves to the n = 2 orbit.

Bohr’s Model of the Atom • The electron releases energy as it falls back towards the ground state.

Bohr’s Model of the Atom • Bohr’s model explained the hydrogen’s spectral lines, but failed to explain any other element’s lines. • For this and other reasons, the Bohr model was replaced with a more sophisticated model called the quantum-mechanical or wavemechanical model.

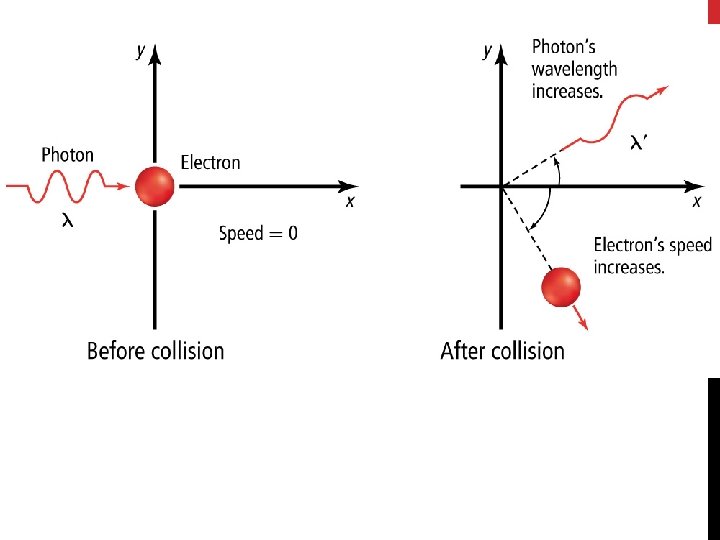
Quantum Mechanical Model • Louis de Broglie (1892– 1987) hypothesized that particles, including electrons, could also have wavelike behaviors. • Electrons do not behave like particles flying through space. • We cannot, in general, describe their exact paths.

Quantum Mechanical Model • Heisenberg showed it is impossible to take any measurement of an object without disturbing it. • The Heisenberg uncertainty principle states that it is fundamentally impossible to know precisely both the velocity and position of a particle at the same time.

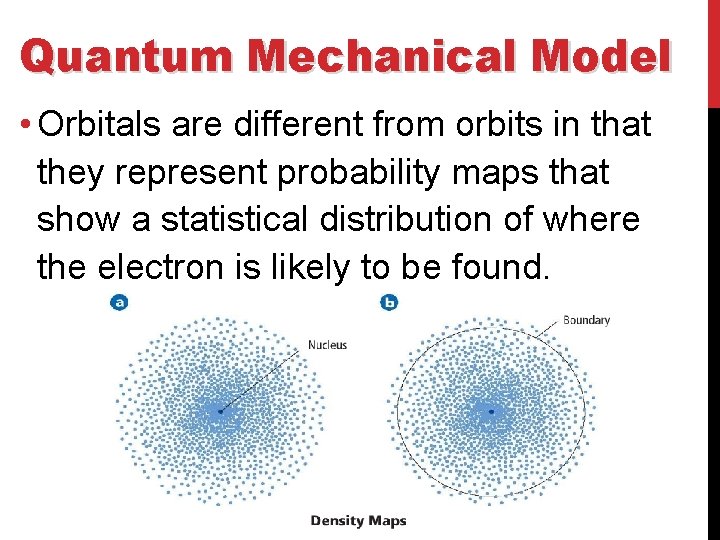
Quantum Mechanical Model • The only quantity that can be known is the probability for an electron to occupy a certain region around the nucleus.

Quantum Mechanical Model • Schrödinger treated electrons as waves in a model called the quantum mechanical model of the atom. • Schrödinger’s equation applied equally well to elements other than hydrogen (unlike Bohr’s model).

Quantum Mechanical Model • The quantum mechanical model makes no attempt to predict the path of an electron around the nucleus. • Bohr orbits were replaced with quantum -mechanical orbitals.

Quantum Mechanical Model • Orbitals are different from orbits in that they represent probability maps that show a statistical distribution of where the electron is likely to be found.

Quantum Mechanical Model • In the quantum-mechanical model, a number and a letter specify an orbital. • The lowest-energy orbital is called the 1 s orbital. • It is specified by the number 1 and the letter s.

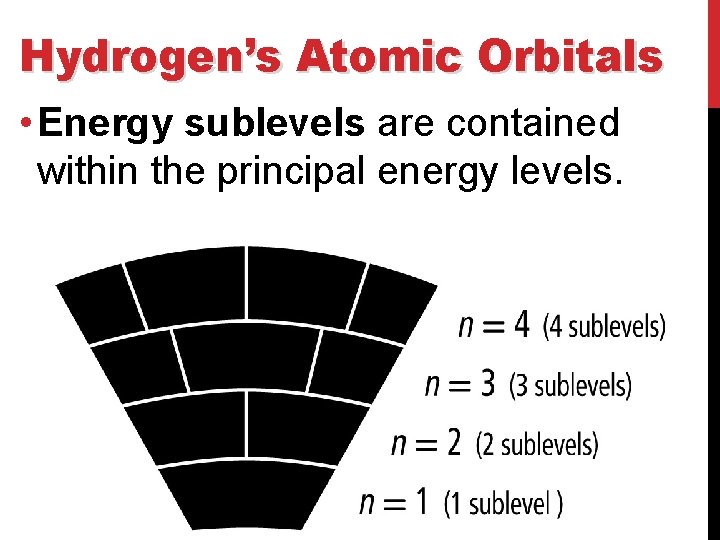
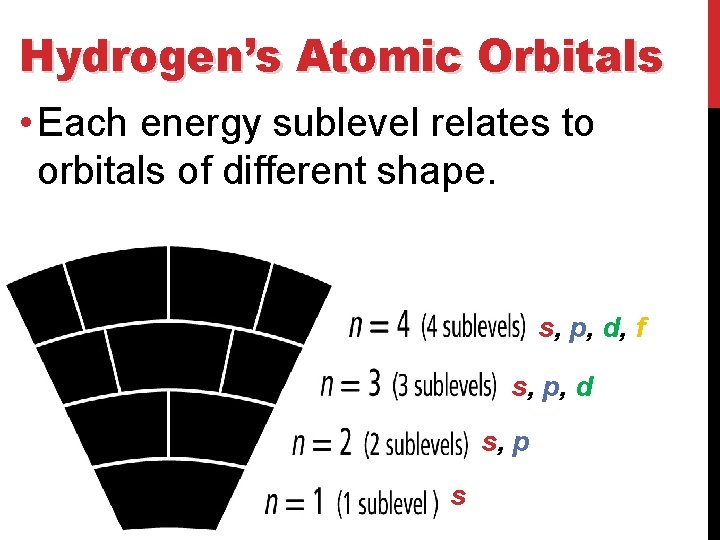
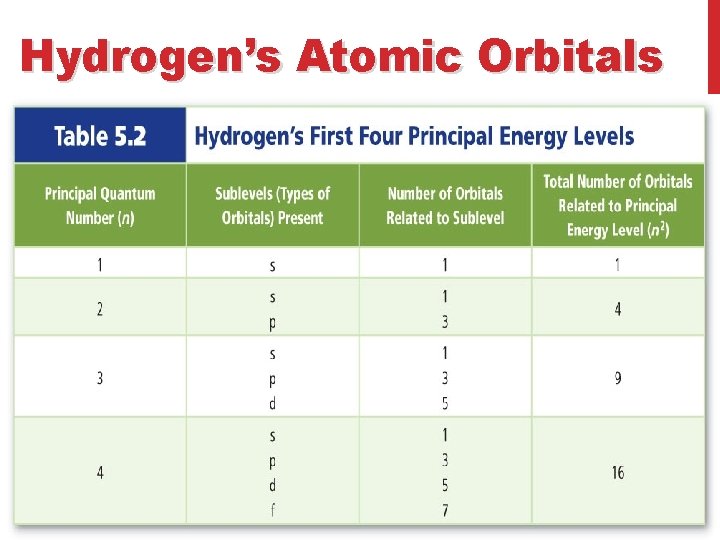
Hydrogen’s Atomic Orbitals • The number is called the Principal quantum number (n) and it indicates the relative size and energy of atomic orbitals. • n specifies the atom’s major energy levels, called the principal energy levels.

Hydrogen’s Atomic Orbitals • Energy sublevels are contained within the principal energy levels.

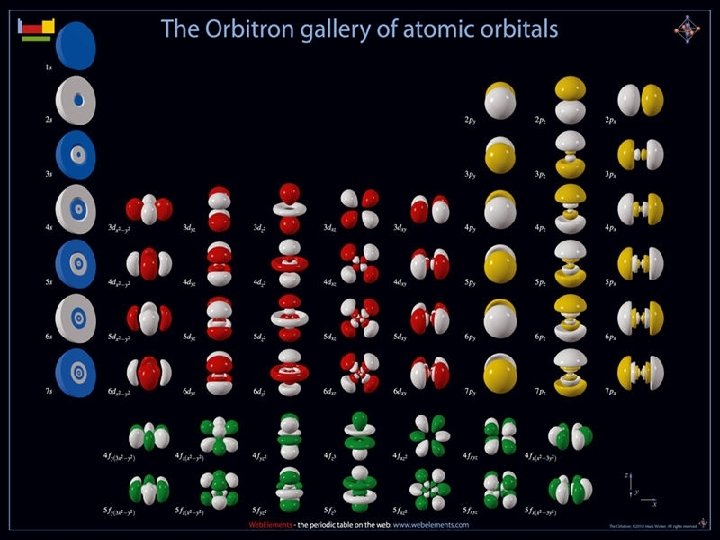
Hydrogen’s Atomic Orbitals • Each energy sublevel relates to orbitals of different shape. s, p, d, f s, p, d s, p s

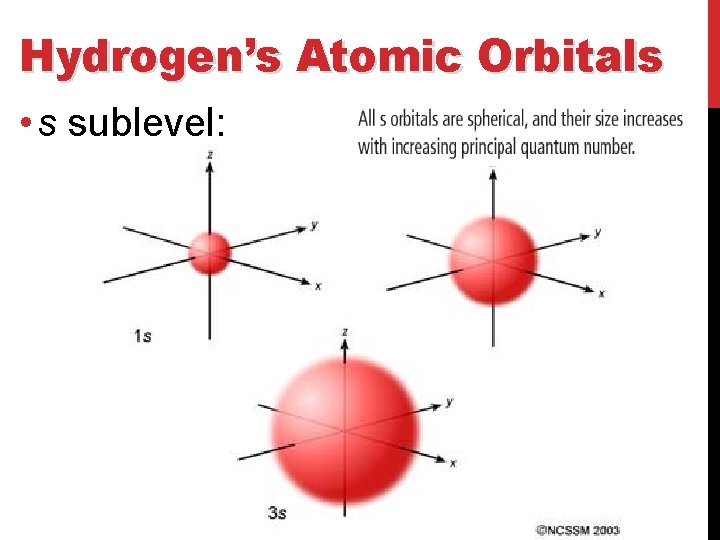
Hydrogen’s Atomic Orbitals • s sublevel:

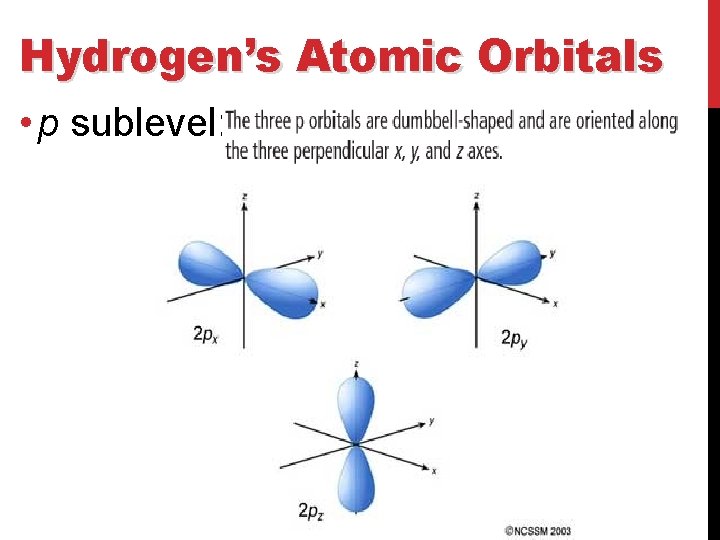
Hydrogen’s Atomic Orbitals • p sublevel:

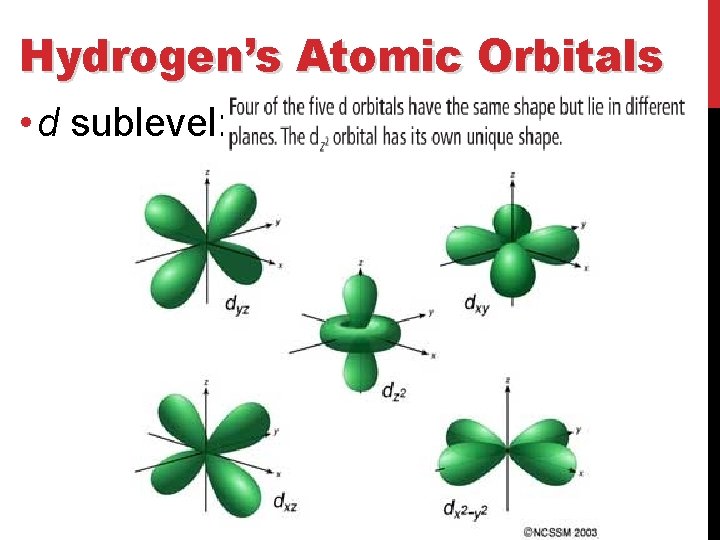
Hydrogen’s Atomic Orbitals • d sublevel:

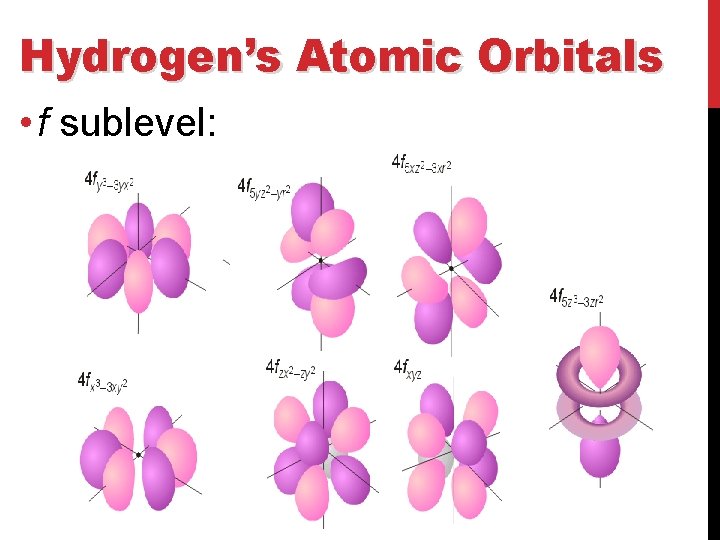
Hydrogen’s Atomic Orbitals • f sublevel:

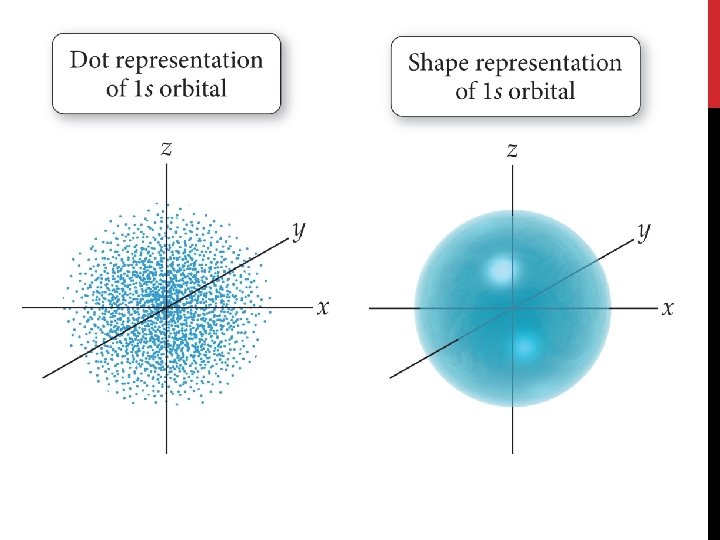
Hydrogen’s Atomic Orbitals • Orbitals are sometimes represented by dots, where the dot density is proportional to the probability of finding the electron. • The dot density for the 1 s orbital is greatest near the nucleus and decreases farther away from the nucleus. • The electron is more likely to be found close to the nucleus than far away from it.

Hydrogen’s Atomic Orbitals

Hydrogen’s Atomic Orbitals • At any given time, hydrogen’s electron can occupy just one orbital. • When hydrogen is in the ground state, the electron occupies the 1 s orbital. • When the atom gains a quantum of energy, the electron is excited to one of the unoccupied orbitals.