Section 2 5 The Normal Distribution Shape of

Section 2. 5 The Normal Distribution

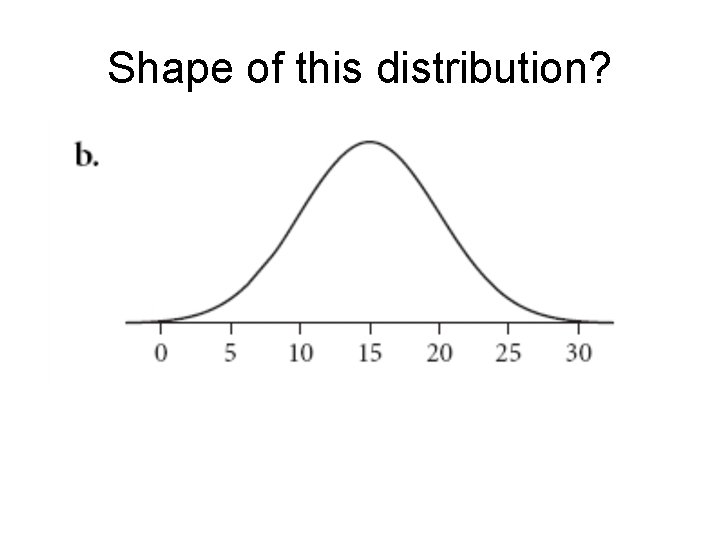
Shape of this distribution?

Normal Distribution If you have a set of data plotted, how do you know you have an approximately normal distribution?

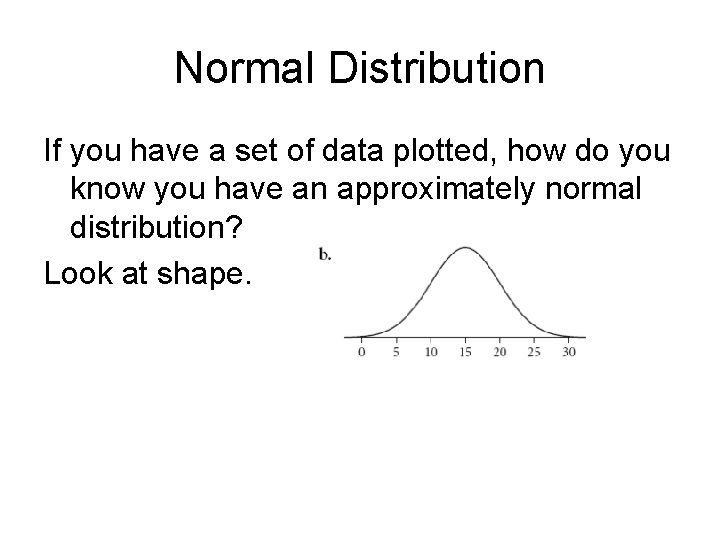
Normal Distribution If you have a set of data plotted, how do you know you have an approximately normal distribution? Look at shape.

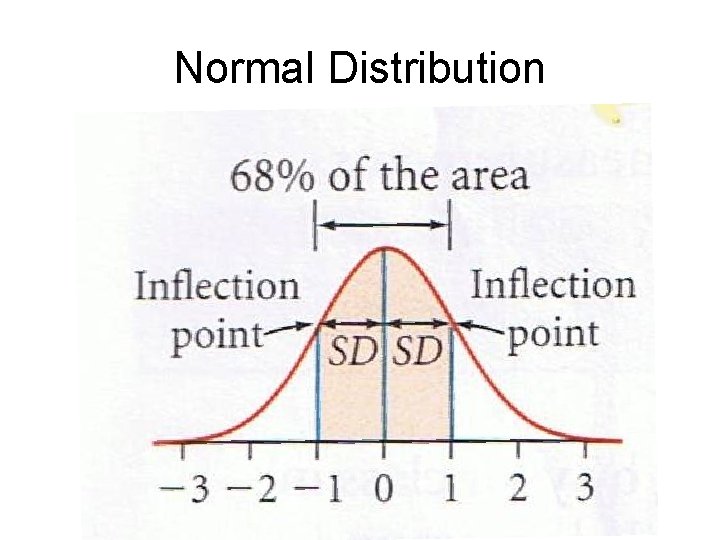
Normal Distribution If you have a set of data plotted, how do you know you have an approximately normal distribution? Look at shape. Should be: (1) bell-shaped curve or mound-shaped (2) most of values in the center (3) fairly symmetric about the center

Normal Distribution If you know the distribution is normal, what other information do you need to know everything else about the distribution?

Normal Distribution If you know the distribution is normal, what other information do you need to know everything else about the distribution? The mean (center) and standard deviation (spread)

Normal Distribution Skewed distributions come in many different shapes, but there is only one normal shape.

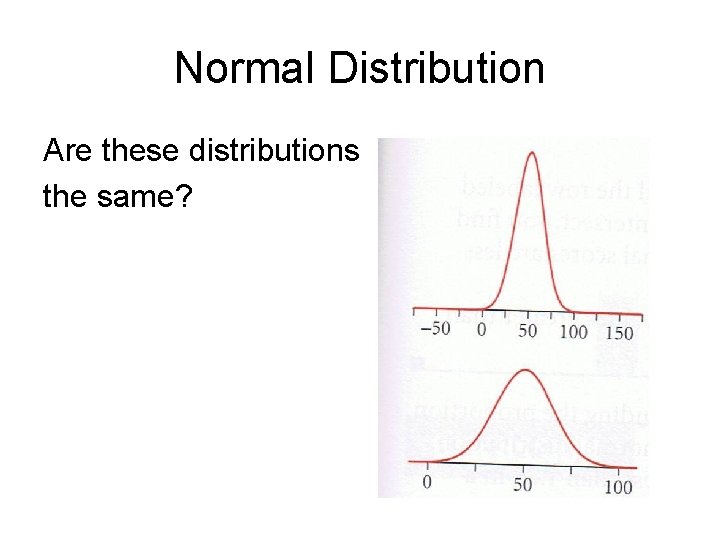
Normal Distribution Are these distributions the same?

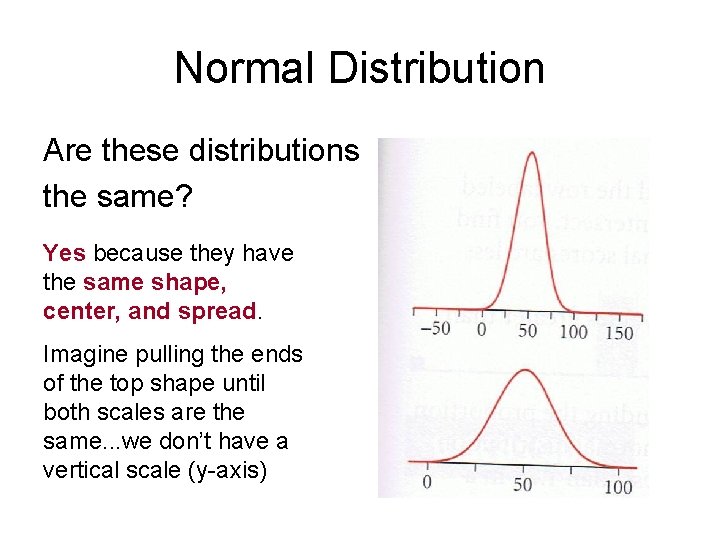
Normal Distribution Are these distributions the same? Yes because they have the same shape, center, and spread. Imagine pulling the ends of the top shape until both scales are the same. . . we don’t have a vertical scale (y-axis)

Normal Distribution

Standard Normal Distribution Standard normal distribution: normal distribution with mean 0 and standard deviation 1 Variable along x-axis is called a z-score

Standard Normal Distribution Negative z-score indicates an individual data element is less than the mean Positive z-score indicates an individual data element is greater than the mean

Standard Normal Distribution So, the sign of the z-score tells us whether we are above or below the mean. The absolute value of the z-score tells us what?

Standard Normal Distribution So, the sign of the z-score tells us whether we are above or below the mean. The absolute value tells us how many standard deviations we are away from the mean.

Standard Normal Distribution Any normal distribution can be converted into a standard normal distribution. How do you do this conversion?

Standard Normal Distribution Any normal distribution can be converted into a standard normal distribution. How do you do this conversion? Use re-centering and re-scaling… Recall: – re-center is adding/subtracting by c and – re-scale is multiplying/dividing by d

Standard Normal Distribution First, re-center all the values of the normal distribution by subtracting the mean from the value of each data element x–x [or x - mean] This gives a distribution with mean = 0

Standard Normal Distribution Second, you re-scale by dividing all the recentered values by the standard deviation. This gives a distribution with mean = 0 and standard deviation = 1.

Z-Score The standard units, or z-score, is the number of standard deviations that a given x-value lies above or below the mean.

Calculating Z-Score The distribution of SAT I math scores for a class was roughly normal with mean 610 and standard deviation 69. What is the z-score for a student who got 560 on the math SAT?

Percentage Under Curve Turn to page 824 in your book or look inside the back cover at Table A.

Find the percentage of values less than z = -3. 87. Think of -3. 87 as -3. 8 and 0. 07 In Table A, find where the row -3. 8 intersects with the column. 07 What value do you see?

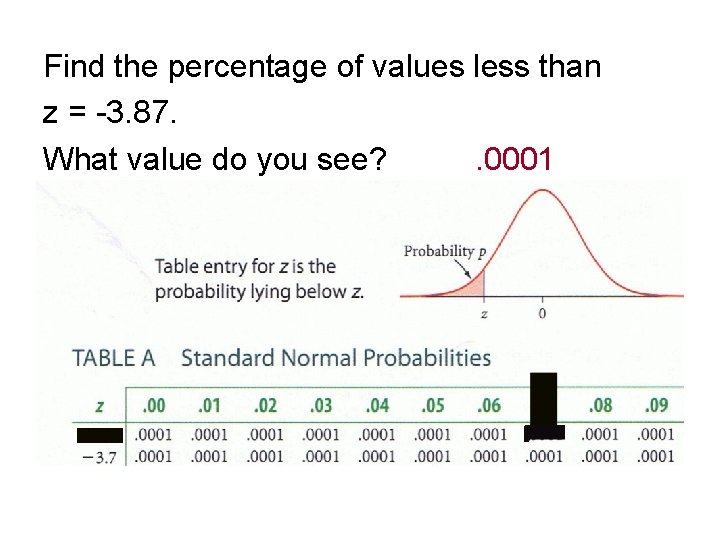
Find the percentage of values less than z = -3. 87. What value do you see? . 0001

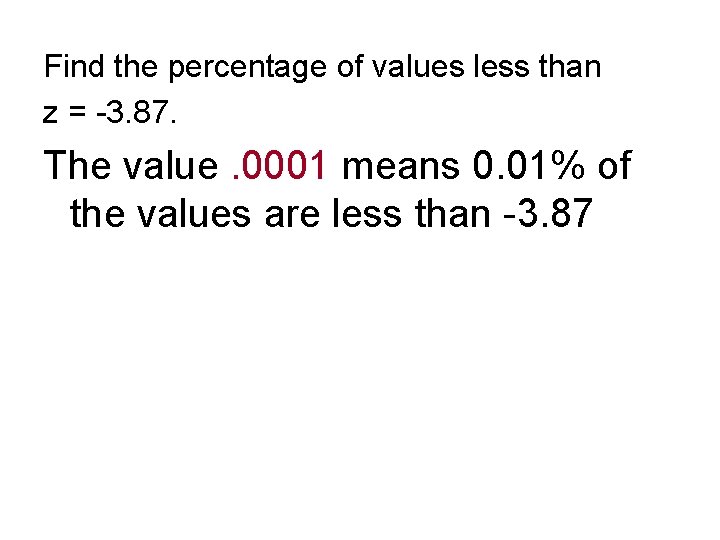
Find the percentage of values less than z = -3. 87. The value. 0001 means 0. 01% of the values are less than -3. 87

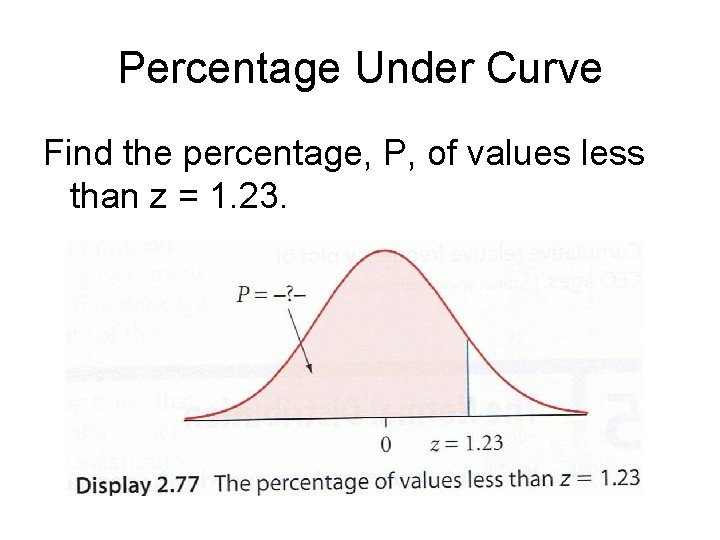
Percentage Under Curve Find the percentage, P, of values less than z = 1. 23.

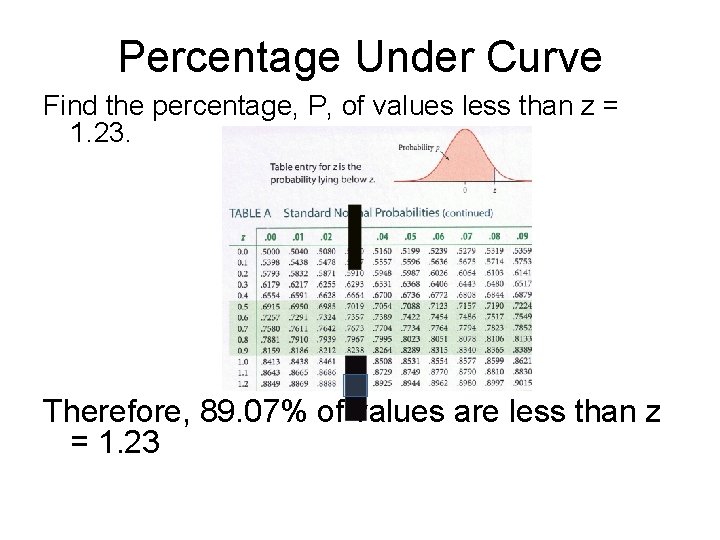
Percentage Under Curve Find the percentage, P, of values less than z = 1. 23. Therefore, 89. 07% of values are less than z = 1. 23

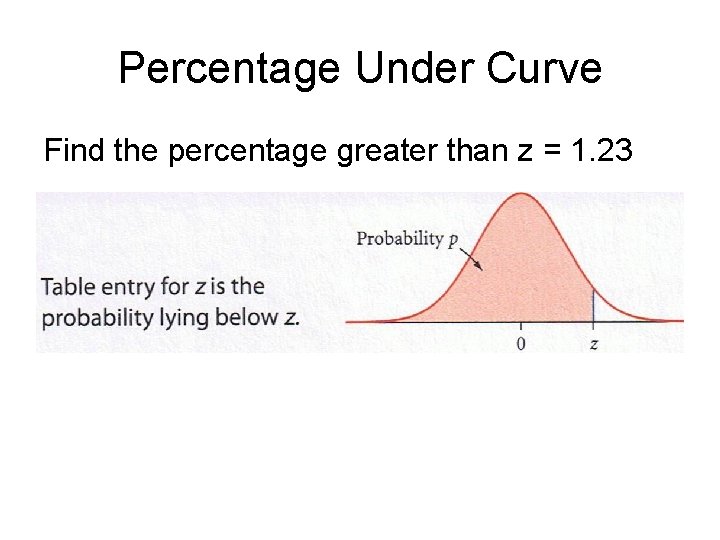
Percentage Under Curve Find the percentage greater than z = 1. 23

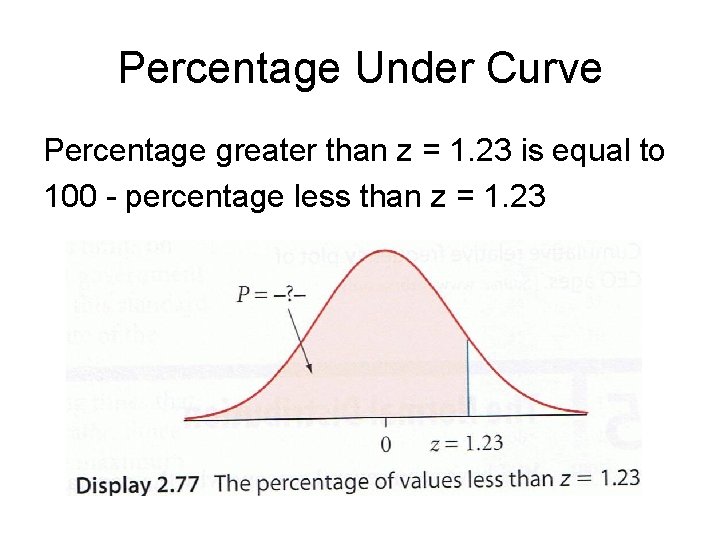
Percentage Under Curve Percentage greater than z = 1. 23 is equal to 100 - percentage less than z = 1. 23

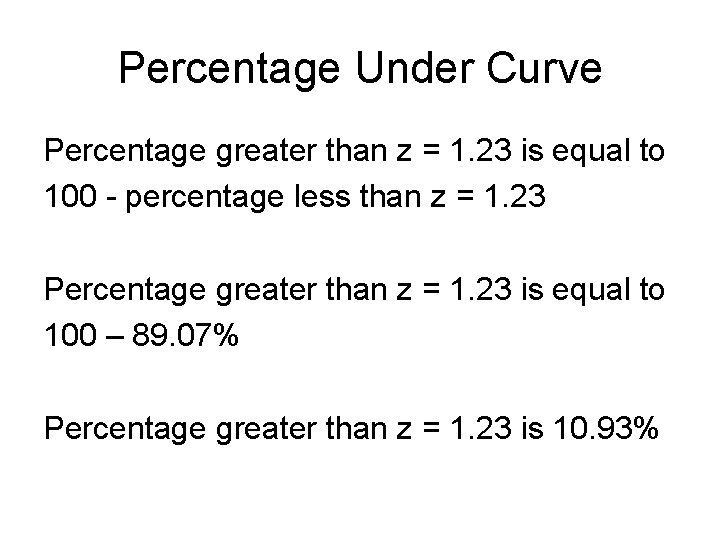
Percentage Under Curve Percentage greater than z = 1. 23 is equal to 100 - percentage less than z = 1. 23 Percentage greater than z = 1. 23 is equal to 100 – 89. 07% Percentage greater than z = 1. 23 is 10. 93%

Use Calculator Instead of using Table A, we can use a graphing calculator. We’ll use normalcdf

Syntax for normalcdf(left bound, right bound, mean, sx)

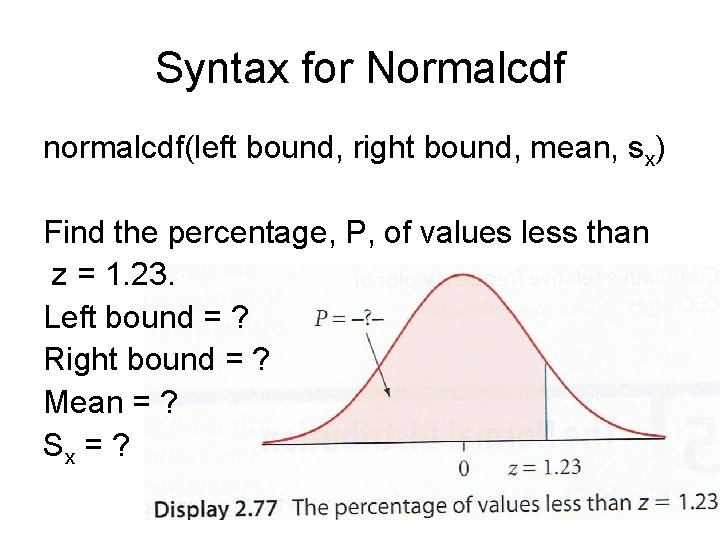
Syntax for Normalcdf normalcdf(left bound, right bound, mean, sx) Find the percentage, P, of values less than z = 1. 23. Left bound = ? Right bound = ? Mean = ? Sx = ?

Syntax for Normalcdf normalcdf(left bound, right bound, mean, sx) Find the percentage, P, of values less than z = 1. 23. Left bound = negative infinity Right bound = Mean = Sx =

Syntax for Normalcdf normalcdf(left bound, right bound, mean, sx) Find the percentage, P, of values less than z = 1. 23. Left bound = -1 EE 99 (use EE button, not E twice) Right bound = Mean = Sx =

Syntax for Normalcdf normalcdf(left bound, right bound, mean, sx) Find the percentage, P, of values less than z = 1. 23. Left bound = -1 EE 99 Right bound = 1. 23 Mean = Sx =

Syntax for Normalcdf normalcdf(left bound, right bound, mean, sx) Find the percentage, P, of values less than z = 1. 23. Left bound = -1 EE 99 Right bound = 1. 23 Mean = 0 Sx =

Syntax for Normalcdf normalcdf(left bound, right bound, mean, sx) Find the percentage, P, of values less than z = 1. 23. Left bound = -1 EE 99 Right bound = 1. 23 Mean = 0 Sx = 1

normalcdf 2 nd Distr Arrow down to 2: normalcdf(-1 EE 99, 1. 23) Enter What is your answer? , press enter

normalcdf 2 nd Distr Arrow down to 2: normalcdf(-1 E 99, 1. 23) Enter , press enter What is your answer? . 8906513833 Round to. 8907 so our answer is 89. 07%

normalcdf What percentage of values is greater than 1. 23? Left bound = ? Right bound = ? Mean = ? Sx = ?

normalcdf What percentage of values is greater than 1. 23? Left bound = 1. 23 Right bound = 1 EE 99 Mean = Sx =

normalcdf What percentage of values is greater than 1. 23? Left bound = 1. 23 Right bound = 1 EE 99 Mean = 0 Sx =

normalcdf What percentage of values is greater than 1. 23? Left bound = 1. 23 Right bound = 1 EE 99 Mean = 0 Sx = 1

normalcdf What percentage of values is greater than 1. 23? Left bound = 1. 23 Right bound = 1 EE 99 Mean = 0 Sx = 1 normalcdf(1. 23, 1 EE 99, 0, 1) =. 1093486167 Answer is 10. 93%

What percentage of values is greater than -1. 23 and less than 1. 23? Left bound = ? Right bound = ? Mean = ? Sx = ?

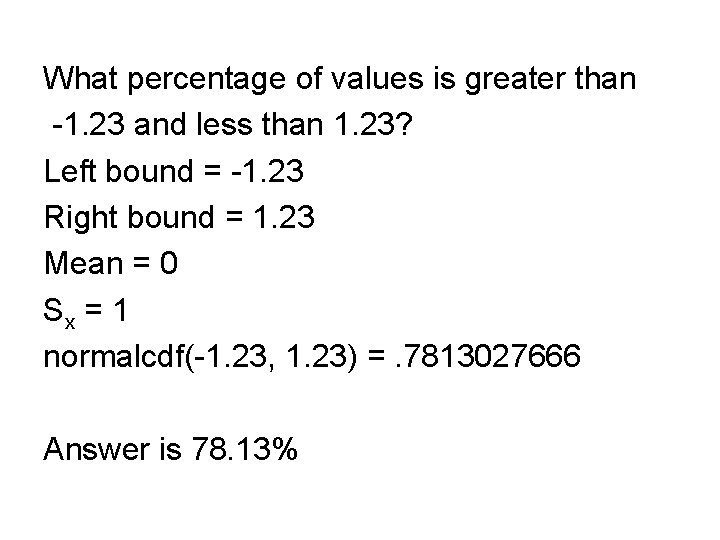
What percentage of values is greater than -1. 23 and less than 1. 23? Left bound = -1. 23 Right bound = 1. 23 Mean = 0 Sx = 1 normalcdf(-1. 23, 1. 23) =. 7813027666 Answer is 78. 13%

Page 92, P 32

Page 92, P 32 a. 1. 29% b. 4. 75% c. 34. 46% d. 78. 81%

Page 93, P 34

Page 93, P 34 a. 0. 8557 or 85. 57% b. 0. 9974 or 99. 74%

Questions?