Section 2 5 Day 2 The Normal Distribution

Section 2. 5 Day 2 The Normal Distribution

normalcdf What percentage of values is greater than 1. 23? Left bound = ? Right bound = ? Mean = ? Sx = ?

normalcdf What percentage of values is greater than 1. 23? Left bound = 1. 23 Right bound = 1 EE 99 Mean = 0 Sx = 1

normalcdf What percentage of values is greater than 1. 23? Left bound = 1. 23 Right bound = 1 EE 99 Mean = 0 Sx = 1 normalcdf(1. 23, 1 EE 99, 0, 1) =. 1093486167 Answer is 10. 93%

Verify that 68% of the values lie within 1 standard deviation of the mean for a normal distribution.

Verify that 68% of the values lie within 1 standard deviation of the mean for a normal distribution. Left bound = -1 Right bound = 1 Mean = 0 Sx = 1

Verify that 68% of the values lie within 1 standard deviation of the mean for a normal distribution. Left bound = -1 Right bound = 1 Mean = 0 Sx = 1 normalcdf(-1, 1) =. 6826894809 Answer is 68. 27%

Finding a Z-Score Find the z-score that has 87% of the values below it in a standard normal distribution.

Finding a Z-Score Find the z-score that has 87% of the values below it in a standard normal distribution. Use inv. Norm

Finding a Z-Score Find the z-score that has 87% of the values below it in a standard normal distribution. Use inv. Norm Syntax: inv. Norm(area, mean, sx)

Finding a Z-Score 2 nd DISTR Arrow down to 3: inv. Norm Enter Inv. Norm( inv. Norm(area, mean, sx) Find the z-score that has 87% of the values below it in a standard normal distribution.

Finding a Z-Score Find the z-score that has 87% of the values below it in a standard normal distribution. inv. Norm(. 87, 0, 1) = 1. 126391128 z = 1. 13

Finding a Z-Score Find the z-score that has 87% of the values below it in a standard normal distribution. inv. Norm(. 87, 0, 1) = 1. 126391128 z = 1. 13 inv. Norm(87, 0, 1) ERR: Syntax

Find Value When Z-Score Known The distribution of SAT I math scores for a class was roughly normal with mean 610 and standard deviation 69. What was a student’s score if her z-score was 1. 6?

Find Value When Z-Score Known The distribution of SAT I math scores for a class was roughly normal with mean 610 and standard deviation 69. What was a student’s score if her z-score was 1. 6? To “unstandardize”, think in reverse.

Find Value When Z-Score Known Which variable do we need to find?

Find Value When Z-Score Known Which variable do we need to find? x = mean + z(SD)

Find Value When Z-Score Known x = mean + z(SD) The distribution of SAT I math scores for a class was roughly normal with mean 610 and standard deviation 69. What was a student’s score if her z-score was 1. 6?

Find Value When Z-Score Known x = mean + z(SD) The distribution of SAT I math scores for a class was roughly normal with mean 610 and standard deviation 69. What was a student’s score if her z-score was 1. 6? x = 610 + (1. 6)(69) = 720. 4

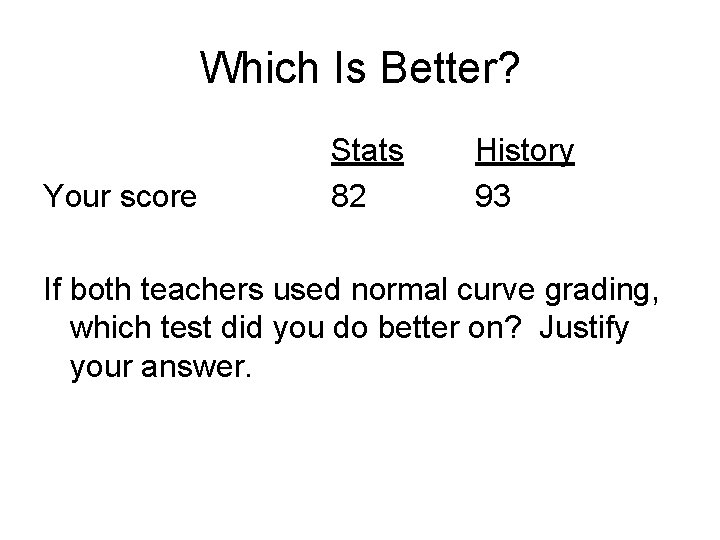
Which Is Better? Your score Stats 82 History 93 If both teachers used normal curve grading, which test did you do better on? Justify your answer.

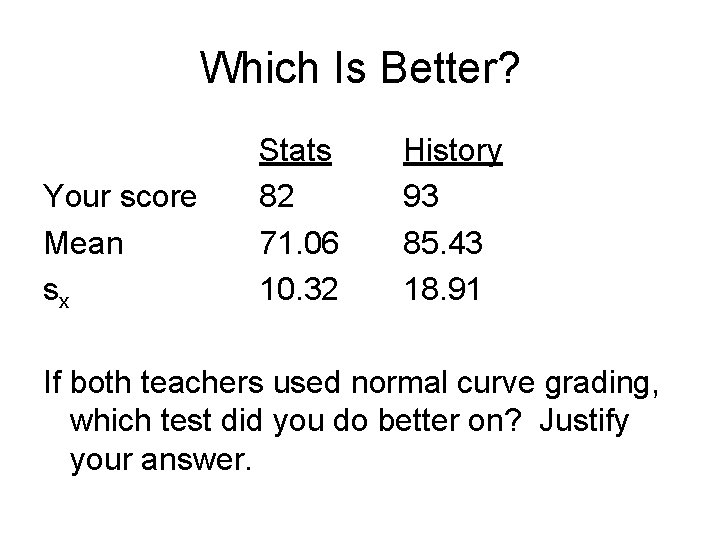
Which Is Better? Your score Mean sx Stats 82 71. 06 10. 32 History 93 85. 43 18. 91 If both teachers used normal curve grading, which test did you do better on? Justify your answer.

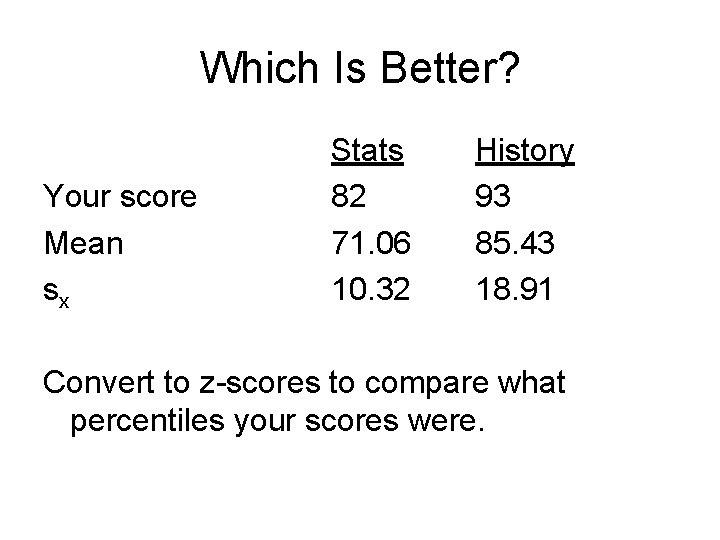
Which Is Better? Your score Mean sx Stats 82 71. 06 10. 32 History 93 85. 43 18. 91 Convert to z-scores to compare what percentiles your scores were.

zs = z. H = Relatively speaking, you did much better on the stats test.

zs = z. H = What percentile were you in for each test? normalcdf(-1 EE 99, z-score)

zs = 86 th percentile z. H = 66 th percentile What percentile were you in for each test? normalcdf(-1 EE 99, z-score)

For groups of similar individuals, heights often are approximately normal. For example, the heights of 18 -to-24 -year-old males in the U. S. are approximately normal, with mean 70. 1 in. and standard deviation 2. 7 in. What percentage of these males are more than 74 in. tall?

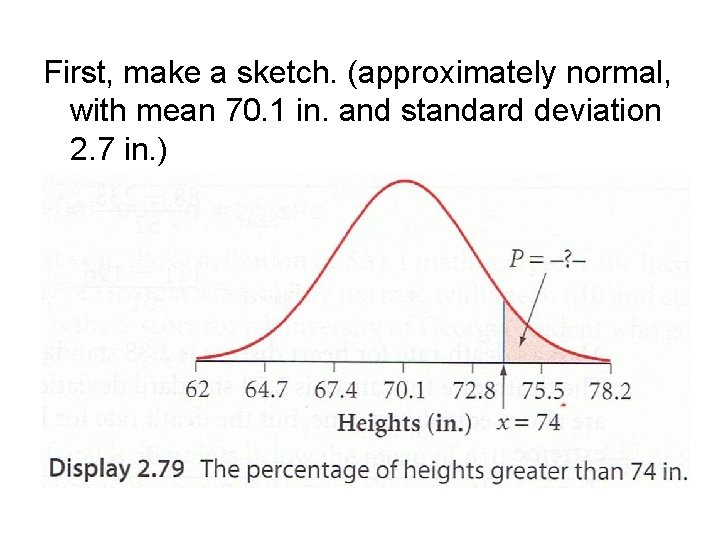
First, make a sketch. (approximately normal, with mean 70. 1 in. and standard deviation 2. 7 in. )

(approximately normal, with mean 70. 1 in. and standard deviation 2. 7 in. ) What percentage of these males are more than 74 in. tall? normalcdf(74, 1 EE 99, 70. 1, 2. 7) = 0. 0743070404 7. 43% of these males are more than 74 in. tall

For groups of similar individuals, heights often are approximately normal. For example, the heights of 18 -to-24 -year-old males in the U. S. are approximately normal, with mean 70. 1 in. and standard deviation 2. 7 in. What percentage of these males are between 72 and 74 in. tall?

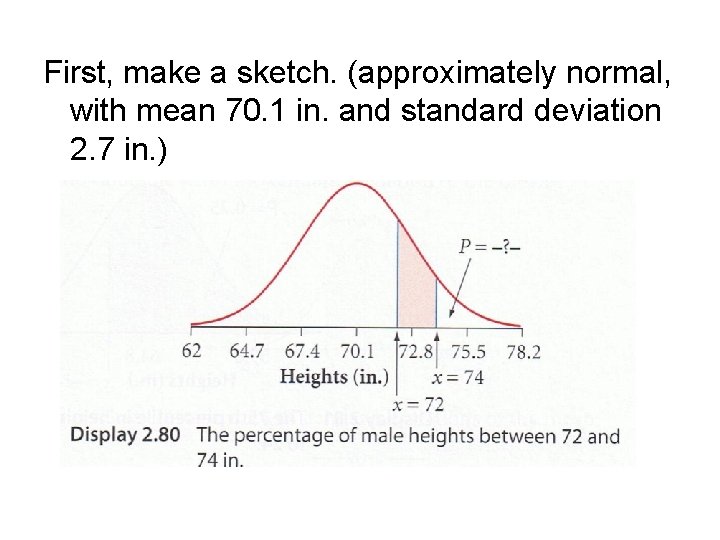
First, make a sketch. (approximately normal, with mean 70. 1 in. and standard deviation 2. 7 in. )

16. 65% of these males are between 72 and 74 in. tall.

The heights of females in the U. S. who are between the ages of 18 and 24 are approximately normally distributed, with mean 64. 8 in. and standard deviation 2. 5 in. What height separates the shortest 75% from the tallest 25%?

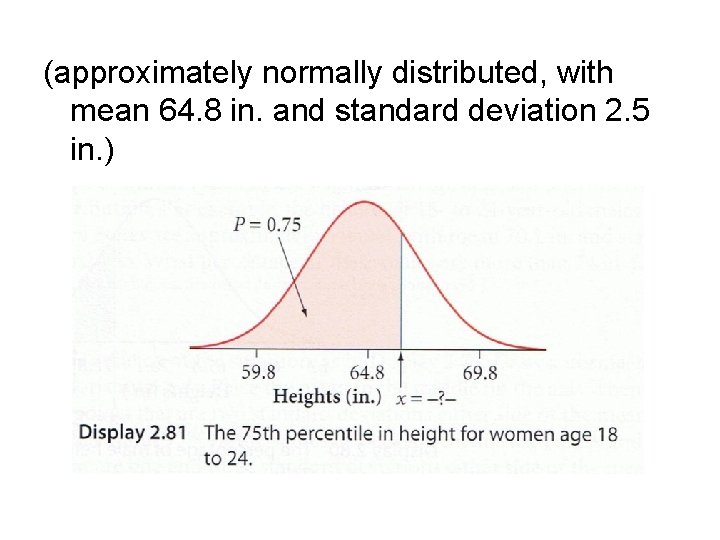
(approximately normally distributed, with mean 64. 8 in. and standard deviation 2. 5 in. )

(approximately normally distributed, with mean 64. 8 in. and standard deviation 2. 5 in. ) What height is the 75 th percentile? x = mean + z(SD)

(approximately normally distributed, with mean 64. 8 in. and standard deviation 2. 5 in. ) What height is the 75 th percentile? x = mean + z(SD) x = 64. 8 + [inv. Norm(. 75)](2. 5)

(approximately normally distributed, with mean 64. 8 in. and standard deviation 2. 5 in. ) What height is the 75 th percentile? x = mean + z(SD) x = 64. 8 + [inv. Norm(. 75)](2. 5) x = 66. 48 in.

(approximately normally distributed, with mean 64. 8 in. and standard deviation 2. 5 in. ) What height is the 75 th percentile? x = mean + z(SD) x = 64. 8 + [inv. Norm(. 75)](2. 5) x = 66. 48 in. Invnorm(. 75, 64. 8, 2. 5)

Question Age of cars. The cars in Clunkerville have a mean age of 12 years and a standard deviation of 8 years. What percentage of cars are more than 4 years old?

Question You can not use the normal distribution to solve this problem because the distribution of the ages of cars is not approximately normal. In fact, it is strongly skewed right.

Question In fact, it is strongly skewed right. The ages can not go below 0 and there is only 1. 5 standard deviations below the mean. So, there must be quite a few ages far out in the upper tail of the distribution.

Page 94, E 64

E 64

E 64 or use inv. Norm(. 8, 511, 112)

Page 93, P 36 a

P 36

Page 93, P 36 c

P 36

Questions?