Section 2 4 Working with Summary Statistics Standard

Section 2. 4 Working with Summary Statistics

Standard Deviation Differences from the mean, x – x, are called deviations. Remember that subtraction means “distance away from. ” So a deviation is the distance a data value “is away from” the mean. The deviation can be positive or negative.

Standard Deviation Differences from the mean, x – x, are called deviations. The Mean is balance point of distribution so the set of deviations from the mean will always sum to zero. ∑(x – x ) = 0 Why? Answer: Half of data values are above the mean (positive

Standard Deviation Formula for standard deviation, s, is: Why are the deviations squared before adding together? Answer: If we square the deviations, then we always get positive numbers to add together…otherwise all the positive and negative deviations would cancel each other out. Why do we divide by “n-1”? Answer: To find the average (mean) of the deviations. . . and we don’t include the mean value as one of the data values. Why do we take the square root? Answer: This “undoes” the squaring of the deviations so that we don’t get the “square of the average of all the deviations” but rather the “average of all the deviations”. . . which is called the variance.

Standard Deviation Formula for standard deviation, s, is: Dividing by n - 1 also gives a slightly larger value than dividing by n. This is useful because otherwise the standard deviation of the sample would tend to be smaller than the standard deviation of the population the sample came from.

Computing Standard Deviation

Computing Standard Deviation Use 1 -Var Stats. Symbol for standard deviation is sx

Summary from Frequency Table [shows percentages (f=frequency) rather than full values]

Summary from Frequency Table

Summary from Frequency Table Enter “values” in List 1 Enter “frequency” in List 2

L 1 L 2

Summary from Frequency Table “STAT”, “CALC”, “ 1: 1 -Var Stats”

Summary from Frequency Table “STAT”, “CALC”, “ 1: 1 -Var Stats” 1 -Var Stats L 1, L 2 Enter

Summary from Frequency Table “STAT”, “CALC”, “ 1: 1 -Var Stats” 1 -Var Stats L 1, L 2 Enter x=4 s = 3. 65

Important Note When homework says to use the formulas to compute something, you may use your calculator instead.

Page 71, P 24 Answer a, b, and c. Use calculator for b and c.

Page 71, P 24 a. Skewed right, or toward the larger values. There is a wall at 0 because no family can have fewer than zero children.

Page 71, P 24 b. median is 3

Page 71, P 24 b. median is 3 c. mean is 3. 24; standard deviation is 1. 89 Construct a boxplot to determine if there any outliers.

Modified Boxplot from Frequency Table

Find Mean & Median A) 1, 2, 3, 4, . . . , 97, 98 B) 1, 2, 3, 4, . . . , 97, 98, 99

Find Mean & Median A) 1, 2, 3, 4, . . . , 97, 98 mean = median’s position = B) 1, 2, 3, 4, . . . , 97, 98, 99

Find Mean & Median B) 1, 2, 3, 4, . . . , 97, 98, 99 mean = 50; median = 50

In a set of data, will the mean and median always be the same? Explain.

In a set of data, will the mean and median always be the same? Explain. To show something is not always true, find a ________.

In a set of data, will the mean and median always be the same? Explain. To show something is not always true, find a counter example.

In a set of data, will the mean and median always be the same? Explain. data: 1, 49, 50 mean = 33. 3; median = 49

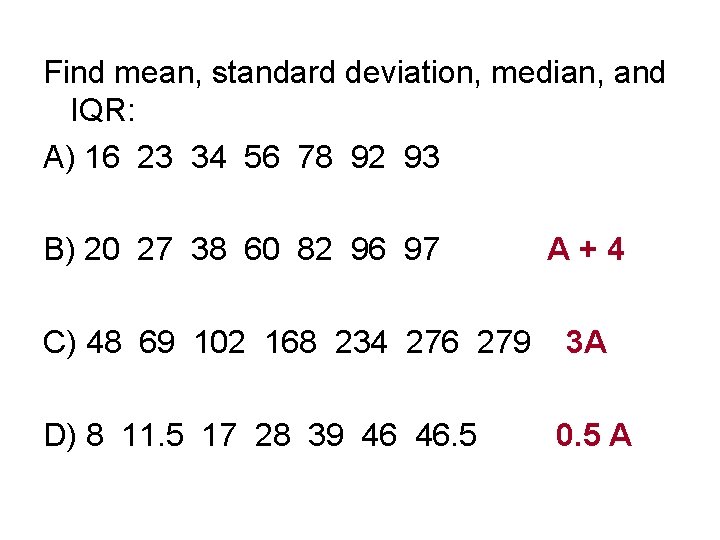
Find mean, standard deviation, median, and IQR: A) 16 23 34 56 78 92 93 B) 20 27 38 60 82 96 97 C) 48 69 102 168 234 276 279 D) 8 11. 5 17 28 39 46 46. 5

Find mean, standard deviation, median, and IQR: A) 16 23 34 56 78 92 93 B) 20 27 38 60 82 96 97 C) 48 69 102 168 234 276 279 D) 8 11. 5 17 28 39 46 46. 5 A+4

Find mean, standard deviation, median, and IQR: A) 16 23 34 56 78 92 93 B) 20 27 38 60 82 96 97 C) 48 69 102 168 234 276 279 D) 8 11. 5 17 28 39 46 46. 5 A+4 3 A

Find mean, standard deviation, median, and IQR: A) 16 23 34 56 78 92 93 B) 20 27 38 60 82 96 97 C) 48 69 102 168 234 276 279 D) 8 11. 5 17 28 39 46 46. 5 A+4 3 A 0. 5 A

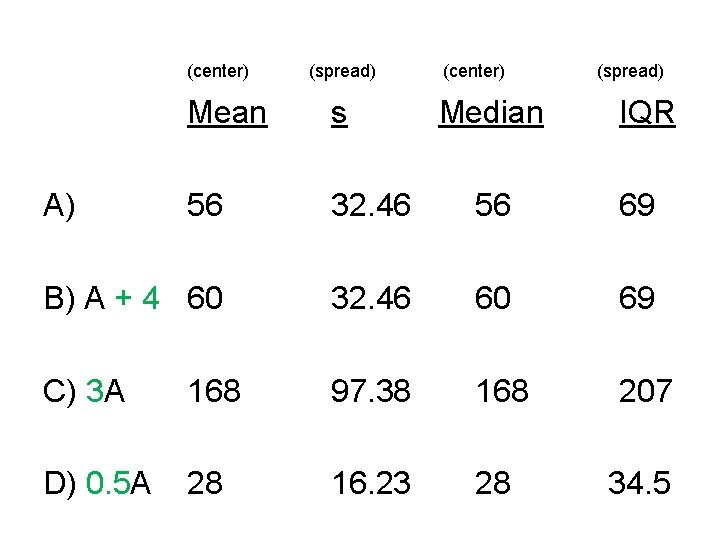
(center) (spread) (center) Mean s 56 32. 46 56 69 B) A + 4 60 32. 46 60 69 C) 3 A 168 97. 38 168 207 D) 0. 5 A 28 16. 23 28 34. 5 A) Median (spread) IQR

Re-centering Adding the same number c to each value in data set does not change the shape or spread.

Re-centering Adding the same number c to each value in data set does not change the shape or spread. Re-centering will slide the whole distribution by the amount c. Think “translation. ” Mean and median change by c. Spread stays the same.

Re-scaling Multiplying each value by the same positive number d does not change the basic shape but stretches or shrinks the distribution. Think “dilation”

Re-scaling Multiplying each value by the same positive number d does not change the basic shape but stretches or shrinks the distribution. Center (mean or median) is multiplied by d. Spread (s or IQR) is multiplied by d.

Influence of Outliers A summary statistic is resistant to outliers if the summary statistic is not changed very much when an outlier is removed from the set of data.

Influence of Outliers If the summary statistic tends to be affected by the removal of outliers, it is sensitive to outliers.

Influence of Outliers Which summary statistics are resistant to outliers? Which summary statistics are sensitive to outliers?

Influence of Outliers Which summary statistics are resistant to outliers? Median and quartiles because these depend on position of values, not the actual numeric values Which summary statistics are sensitive to outliers?

Influence of Outliers Which summary statistics are resistant to outliers? Median and quartiles Which summary statistics are sensitive to outliers? Mean and standard deviation because these depend on the actual numeric values

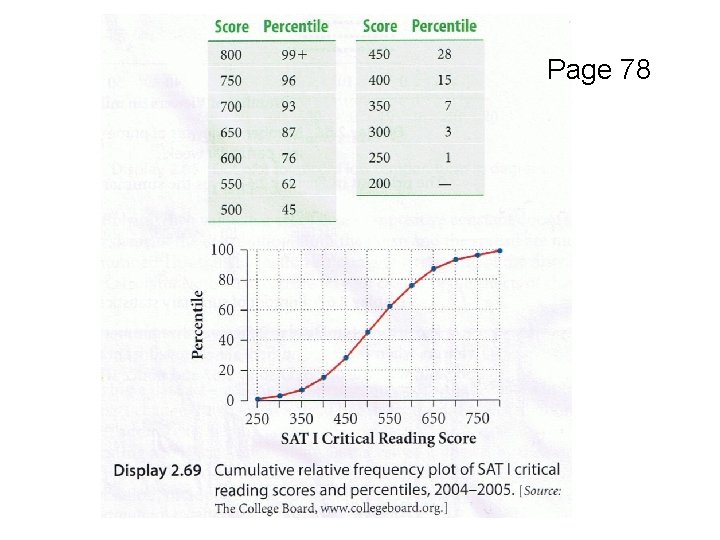
Percentiles and Cumulative Relative Frequency Plots Percentiles measure position within a data set.

Percentiles and Cumulative Relative Frequency Plots Percentiles measure position within a data set. Q 1 is 25 th percentile - - the value that separates the lowest 25% of the ordered values from the rest Median is 50 th percentile Q 3 is the 75 th percentile

Percentiles and Cumulative Relative Frequency Plots In general, a value is at the kth percentile if k% of all values are less than or equal to it.

Page 78

Suppose you have a set of univariate data (data that involves a single variable per case). The data consists of the weights of the students in a class. What are the cases? What is the variable?

Suppose you have a set of univariate data (data that involves a single variable per case). The data consists of the weights of the students in a class. What are the cases? Individual students What is the variable?

Suppose you have a set of univariate data (data that involves a single variable per case). The data consists of the weights of the students in a class. What are the cases? Individual students What is the variable? The weight for each student

The data consists of the weights of the students in a class. List all the measures you know to describe the data set.

List all the measures you know to describe the data set. x, sx, median, Q 1, Q 3, min, max, range, IQR, mode, and outliers Now categorize these measures in terms of describing shape, center, or spread.

List all the measures you know to describe the data set. x, sx, median, Q 1, Q 3, min, max, range, IQR, mode, and outliers Now categorize these measures in terms of describing shape, center, or spread. None of these describe the shape.

How do you describe the shape?

How do you describe the shape? Uniform distribution, normal distribution, skewed left, skewed right Bimodal Recall: 1. plot → 2. shape → 3. center → 4. spread

Plot this data into stem-and-leaf plot: 23, 125, 8, 23, 50 Determine: shape, center, spread

Plot this data into stem-and-leaf plot: 23, 125, 8, 23, 50 0 2 5 12 8 3 3 0 5 5 0 represents 50 Shape: skewed right, median=23, Q 1=15. 5, Q 3=67. 5, IQR=52, outlier=125

Questions?