Section 2 3 Venn Diagrams and Set Operations



























- Slides: 31

Section 2. 3 Venn Diagrams and Set Operations Copyright 2013, 2010, 2007, Pearson, Education, Inc.

What You Will Learn Venn diagrams 2. 3 -2 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Venn Diagrams A Venn diagram is a useful technique for illustrating set relationships. • Named for John Venn. • Venn invented and used them to illustrate ideas in his text on symbolic logic. • 2. 3 -3 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Venn Diagrams A rectangle usually represents the universal set, U. • The items inside the rectangle may be divided into subsets of U and are represented by circles. • The circle labeled A represents set A. • 2. 3 -4 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Disjoint Sets Two sets which have no elements in common are said to be disjoint. • The intersection of disjoint sets is the empty set. • There are no elements in common since there is no overlapping area between the two circles. • 2. 3 -5 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

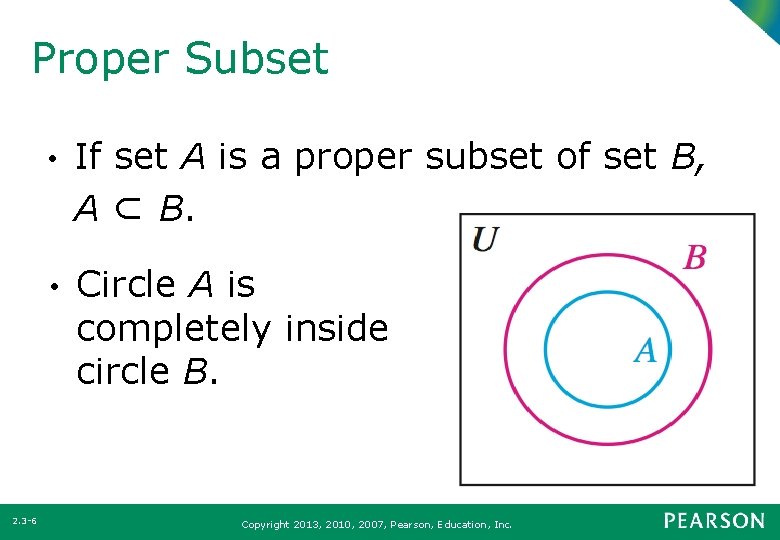
Proper Subset 2. 3 -6 • If set A is a proper subset of set B, A ⊂ B. • Circle A is completely inside circle B. Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Equal Sets If set A contains exactly the same elements as set B, A = B. • Both sets are drawn as one circle. • 2. 3 -7 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

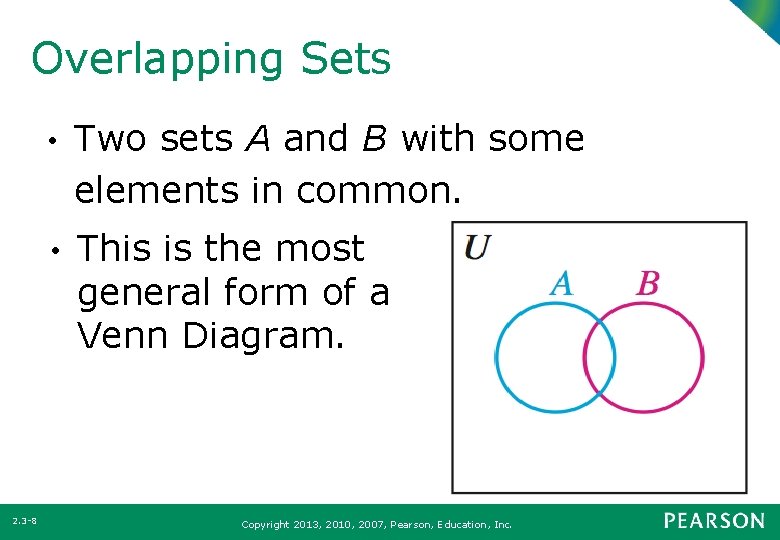
Overlapping Sets 2. 3 -8 • Two sets A and B with some elements in common. • This is the most general form of a Venn Diagram. Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Case 1: Disjoint Sets A and B, are disjoint, they have no elements in common. • Region II is empty. • 2. 3 -9 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Case 2: Subsets 2. 3 -10 • When A ⊆ B, every element of set A is also an element of set B. • Region I is empty. • If B ⊆ A, however, then region III is empty. Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Case 3: Equal Sets When set A = set B, all elements of set A are elements of set B and all elements of set B are elements of set A. • Regions I and III are empty. • 2. 3 -11 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Case 4: Overlapping Sets When sets A and B have elements in common, those elements are in region II. • Elements that belong to set A but not to set B are in region I. • Elements that belong to set B but not to set A are in region III. • 2. 3 -12 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

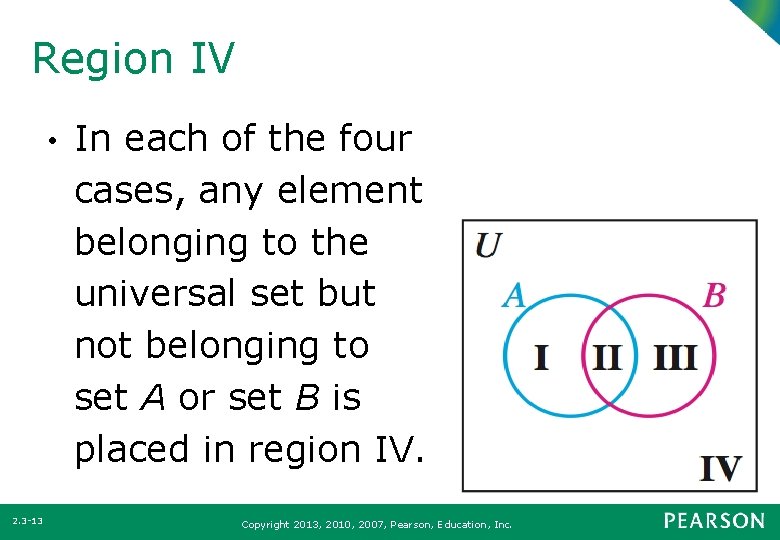
Region IV • 2. 3 -13 In each of the four cases, any element belonging to the universal set but not belonging to set A or set B is placed in region IV. Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Complement of a Set • 2. 3 -14 The complement of set A, symbolized A´, is the set of all elements in the universal set that are not in set A. Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 1: A set and Its Complement Given U = {1, 2, 3, 4, 5, 6, 7, 8} and A = { 1, 3, 4} Find A and illustrate the relationship among sets U, A, and A´ in a Venn diagram. 2. 3 -15 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 1: A set and Its Complement Solution U = {1, 2, 3, 4, 5, 6, 7, 8} and A = { 1, 3, 4} All of the elements in U that are not in set A are 2, 5, 6, 7, 8. Thus, A´ = {2, 5, 6, 7, 8}. 2. 3 -16 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

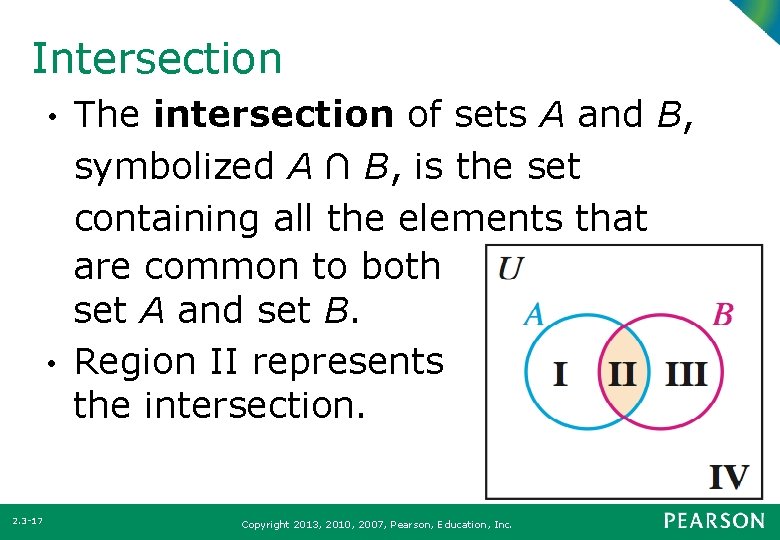
Intersection The intersection of sets A and B, symbolized A ∩ B, is the set containing all the elements that are common to both set A and set B. • Region II represents the intersection. • 2. 3 -17 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 3: Intersection of Sets Given U = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10} A = { 1, 2, 3, 8} B = {1, 3, 6, 7, 8} C={} Find a) A ⋂ B c) A´⋂ B 2. 3 -18 b) A ⋂ C d) (A ⋂ B)´ Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 3: Intersection of Sets Solution U = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10} A = { 1, 2, 3, 8} B = {1, 3, 6, 7, 8} C={} a) A⋂B = {1, 2, 3, 8} ⋂ {1, 3, 6, 7, 8} The elements common to both set A and B are 1, 3, and 8. 2. 3 -19 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 3: Intersection of Sets Solution U = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10} A = { 1, 2, 3, 8} B = {1, 3, 6, 7, 8} C={} b) A ⋂ C = {1, 2, 3, 8} ⋂ { } There are no elements common to both set A and C. 2. 3 -20 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 3: Intersection of Sets Solution U = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10} A = { 1, 2, 3, 8} B = {1, 3, 6, 7, 8} c) A´ ⋂ B First determine A´ A´ = {4, 5, 6, 7, 9, 10} A´ ⋂ B = {4, 5, 6, 7, 9, 10} ⋂ {1, 3, 6, 7, 8} = {6, 7} 2. 3 -21 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 3: Intersection of Sets Solution U = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10} A = { 1, 2, 3, 8} B = {1, 3, 6, 7, 8} d) (A ⋂ B)´ First determine A ⋂ B = {1, 3, 8} (A ⋂ B)´= {1, 3, 8}´ = {2, 4, 5, 6, 7, 9, 10} 2. 3 -22 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Try This: Use the information to find the solutions U = {a, b, c, d, e, f, g, h} A = { a, d, h} B = {b, c, d, e} 2. 3 -23 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Union • The union of sets A and B, symbolized A ⋃ B, is the set containing all the elements that are members of set A or of set B (or of both sets). • Regions I, II, and III represents the union. 2. 3 -24 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 5: The Union of Sets Given U = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10} A = { 1, 2, 4, 6} B = {1, 3, 6, 7, 9} C={} Find a) A ⋃ B c) A´⋃ B 2. 3 -25 b) A ⋃ C d) (A ⋃ B)´ Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 5: The Union of Sets Solution U = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10} A = {1, 2, 4, 6} B = {1, 3, 6, 7, 9} C={} a) A ⋃ B = {1, 2, 4, 6}⋃{1, 3, 6, 7, 9} = {1, 2, 3, 4, 6, 7, 9} 2. 3 -26 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 5: The Union of Sets Solution U = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10} A = {1, 2, 4, 6} B = {1, 3, 6, 7, 9} C={} b) A ⋃ C = {1, 2, 4, 6} ⋃ { } = {1, 2, 4, 6} Note that A ⋃ C = A. 2. 3 -27 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 5: The Union of Sets Solution U = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10} A = {1, 2, 4, 6} B = {1, 3, 6, 7, 9} c) A´ ⋃ B First determine A´ A´ = {3, 5, 7, 8, 9, 10} A´ ⋃ B = {3, 5, 7, 8, 9, 10} ⋃ {1, 3, 6, 7, 9} = {1, 3, 5, 6, 7, 8, 9, 10} 2. 3 -28 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 5: The Union of Sets Solution U = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10} A = {1, 2, 4, 6} B = {1, 3, 6, 7, 9} d) (A ⋃ B)´ First determine A ⋃ B = {1, 2, 3, 4, 6, 7, 9} (A ⋃ B)´= {1, 2, 3, 4, 6, 7, 9}´ = {5, 8, 10} 2. 3 -29 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Try This: Use the information to find the solutions U = {a, b, c, d, e, f, g, h} A = { a, d, h} B = {b, c, d, e} 2. 3 -30 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Homework p. 64 # 9 – 69 (x 3) Ch. 2. 1 – 2. 2 Quiz next class 2. 3 -31 Copyright 2013, 2010, 2007, Pearson, Education, Inc.