SECTION 2 3 Quadratic Functions DEFINITION A quadratic

SECTION 2. 3 Quadratic Functions

DEFINITION A quadratic function is a function of the form f(x) = ax 2 + bx + c Where a, b, and c are real numbers with a ≠ 0 The domain of a quadratic function is (-∞, ∞)

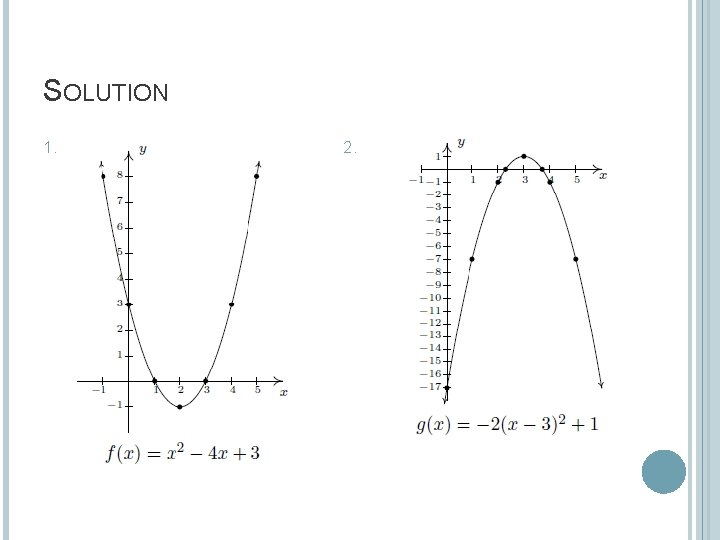
EXAMPLE Graph each of the following quadratic functions. Find the zeros of each function and the x- and yintercepts of each graph, if any exist. From the graph, determine the domain and range of each function, list the intervals on which the function is increasing, decreasing, or constant and find the relative and absolute extrema, if they exist 1. 2. f(x) = x 2 - 4 x + 3 g(x) = -2(x – 3)2 + 1

SOLUTION 1. 2.

GRAPHS OF QUADRATIC EQUATIONS 1. 2. 3. 4. The graph of y = ax 2 + bx + c where a, b, and c are real numbers with a ≠ 0 is called a parabola The coefficient of x 2, a, positive, the parabola opens upwards negative, it opens downwards The point at which the relative minimum (a > 0) or relative maximum (a < 0) occurs is called the vertex of the parabola The parabolas are symmetric about the dashed vertical line which contains its vertex (axis of symmetry)

VERTEX FORMULAS FOR QUADRATIC FUNCTIONS Suppose a, b, c, h, and k are real numbers with a ≠ 0 If f(x) = a(x - h)2 + k (standard form), the vertex of the graph of y = f(x) is the point (h, k) If f(x) = ax 2 + bx + c (general form), the vertex of the graph of y = f(x) is the point Example: Find the vertex of the graphs 1. 2. f(x) = x 2 - 4 x + 3 g(x) = -2(x – 3)2 + 1

QUADRATIC FORMULA If a, b, c are real numbers with a ≠ 0, then the solutions to ax 2 + bx + c = 0 are

EXAMPLE The profit function for a product is defined by the equation Profit = Revenue-Cost, or P(x) = R(x) - C(x) The weekly revenue, in dollars, made by selling x Porta. Boy Game Systems is given by R(x) = -1. 5 x 2 + 250 x The cost, in dollars, to produce x Porta. Boy Game Systems is given as C(x) = 80 x + 150, x ≥ 0 Determine the weekly profit function, P(x) Graph y = P(x). Include the x- and y-intercepts as well as the vertex and axis of symmetry Interpret the zeros of P Interpret the vertex of the graph of y = P(x) Recall the weekly price-demand equation for Porta. Boys is: p(x) = -1. 5 x+250, where p(x) is the price per Porta. Boy, in dollars, and x is the weekly sales. What should the price per system be in order to maximize profit?

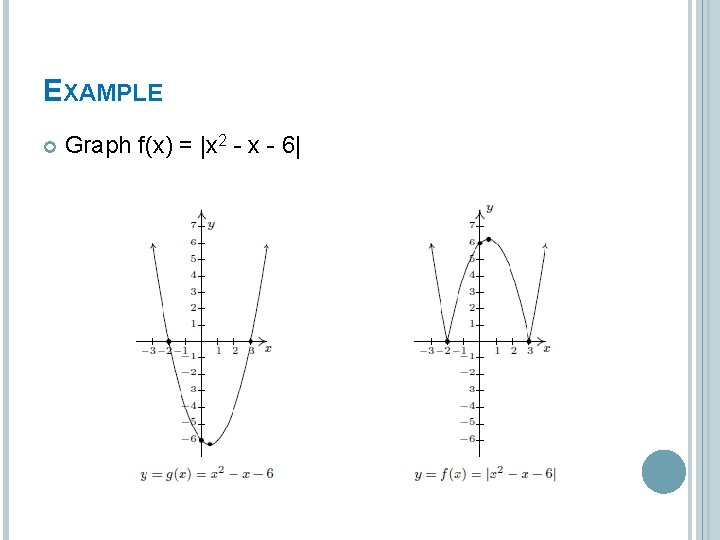
EXAMPLE Graph f(x) = |x 2 - x - 6|