SECTION 2 2 Graphs of Equations OBJECTIVES 1

SECTION 2. 2 Graphs of Equations OBJECTIVES 1 Sketch a graph by plotting points. 2 Find the intercepts of a graph. 3 Find the symmetries in a graph. 4 Find the equation of a circle. Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Definition s An ordered pair (a, b) is said to satisfy an equation with variables a and b if, when a is substituted for x and b is substituted for y in the equation, the resulting statement is true. An ordered pair that satisfies an equation is called a solution of the equation. Frequently, the numerical values of the variable y can be determined by assigning appropriate values to the variable x. For this reason, y is sometimes referred to as the dependent variable and x as the independent variable. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 2

GRAPH OF AN EQUATION The graph of an equation in two variables, such as x and y, is the set of all ordered pairs (a, b) in the coordinate plane that satisfy the equation. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 3
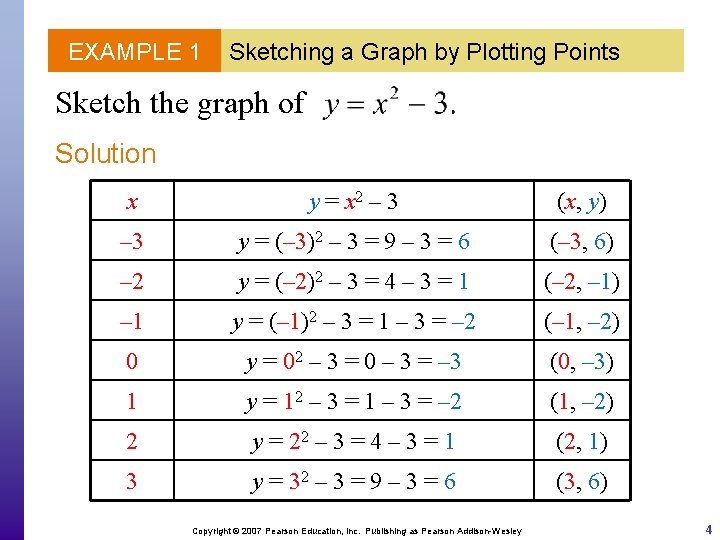
EXAMPLE 1 Sketching a Graph by Plotting Points Sketch the graph of Solution x y = x 2 – 3 (x, y) – 3 y = (– 3)2 – 3 = 9 – 3 = 6 (– 3, 6) – 2 y = (– 2)2 – 3 = 4 – 3 = 1 (– 2, – 1) – 1 y = (– 1)2 – 3 = 1 – 3 = – 2 (– 1, – 2) 0 y = 02 – 3 = 0 – 3 = – 3 (0, – 3) 1 y = 12 – 3 = 1 – 3 = – 2 (1, – 2) 2 y = 22 – 3 = 4 – 3 = 1 (2, 1) 3 y = 32 – 3 = 9 – 3 = 6 (3, 6) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 4
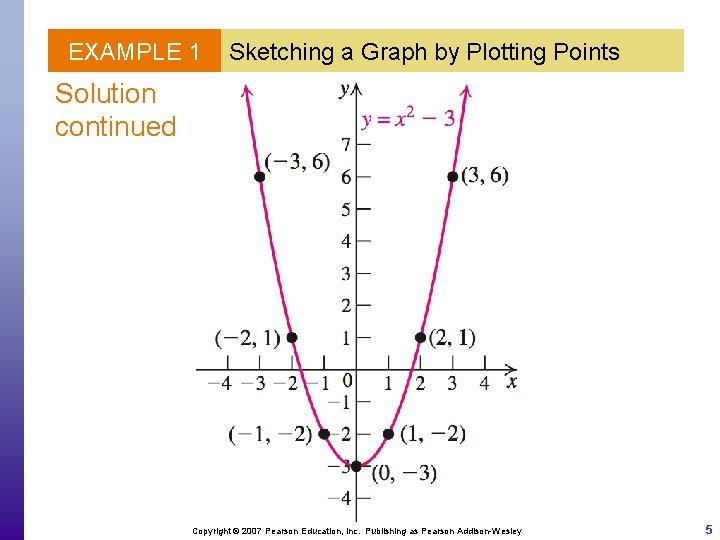
EXAMPLE 1 Sketching a Graph by Plotting Points Solution continued Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 5

SKETCHING A GRAPH BY PLOTTING POINTS Step 1. Make a representative table of solutions of the equation. Step 2. Plot the solutions as ordered pairs in the Cartesian coordinate plane. Step 3. Connect the solutions in Step 2 by a smooth curve. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 6

Definition s The points where a graph intersects (crosses or touches) the coordinate axes are of special interest in many problems. Since all points on the x-axis have a y-coordinate of 0, any point where a graph intersects the x-axis has the form (a, 0). The number a is called an x-intercept of the graph. Similarly, any point where a graph intersects the y-axis has the form (0, b), and the number b is called a y-intercept of the graph. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 7

PROCEDURE FOR FINDING THE INTERCEPTS OF A GRAPH Step 1 To find the x-intercepts of an equation, set y = 0 in the equation and solve for x. Step 2 To find the y-intercepts of an equation, set x = 0 in the equation and solve for y. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 8

EXAMPLE 2 Finding Intercepts Find the x- and y-intercepts of the graph of the equation y = x 2 – x – 2. Solution Step 1 To find the x-intercepts, set y = 0, solve for x. The x-intercepts are – 1 and 2. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 9

EXAMPLE 2 Finding Intercepts Solution continued Step 2 To find the y-intercepts, set x = 0, solve for y. The y-intercept is – 2. This is the graph of the equation y = x 2 – x – 2. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 10

Definition s A useful tool for sketching the graph of an equation is the concept of symmetry, which means that one portion of the graph is a mirror image of another portion. The mirror line is usually called the axis of symmetry or line of symmetry. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 11
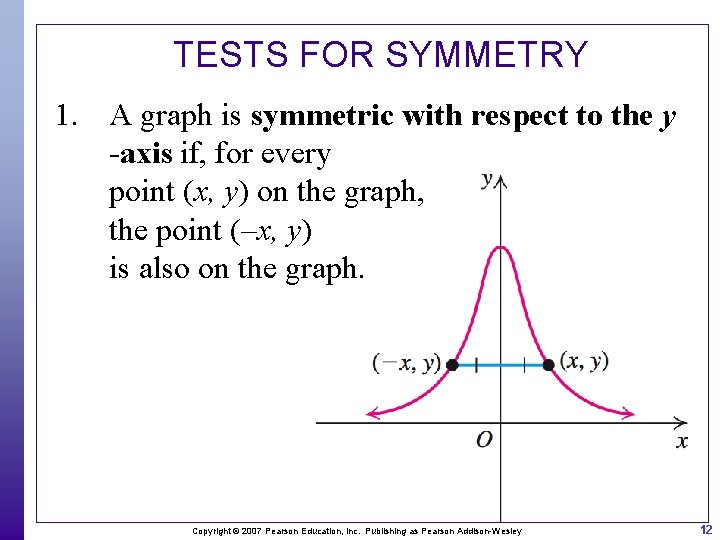
TESTS FOR SYMMETRY 1. A graph is symmetric with respect to the y -axis if, for every point (x, y) on the graph, the point (–x, y) is also on the graph. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 12

TESTS FOR SYMMETRY 2. A graph is symmetric with respect to the x -axis if, for every point (x, y) on the graph, the point (x, –y) is also on the graph. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13

TESTS FOR SYMMETRY 3. A graph is symmetric with respect to the origin if, for every point (x, y) on the graph, the point (–x, –y) is also on the graph. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 14

EXAMPLE 3 Checking for Symmetry Determine whether the graph of the equation is symmetric with respect to the y-axis. Solution Replace x with –x in the original equation. When we replace x with –x in the equation, we obtain the original equation. The graph is symmetric with respect to the y-axis. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 15

EXAMPLE 4 Checking for Symmetry Show that the graph of is symmetric with respect to the x-axis. Solution Replace y with –y in the original equation. When we replace y with –y in the equation, we obtain the original equation. The graph is symmetric with respect to the x-axis. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 16

EXAMPLE 5 Checking for Symmetry with Respect to the Origin Show that the graph of is symmetric with respect to the origin, but not with respect to either axis. Solution Replace x with –x and y with –y. Replacing x with –x and y with –y in the equation, we obtain the original equation. The graph is symmetric with respect to the origin. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 17

EXAMPLE 5 Checking for Symmetry with Respect to the Origin Solution continued The graph of y 5 = x 3 is not symmetric with respect to the y-axis because the point (1, 1) is on the graph, but the point (– 1, 1) is not on the graph. Similarly, the graph of y 5 = x 3 is not symmetric with respect to the x-axis since the point (1, 1) is on the graph, but the point (1, – 1) is not on the graph. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 18

EXAMPLE 6 Sketching a Graph by Using Intercepts and Symmetry Initially, there are 400 deer on Dooms island. The number y of deer on the island after t years is described by the equation a. Sketch the graph of the equation b. Adjust the graph in part (a) to account for only the physical aspects of the problem. c. When does the population of deer become extinct on Dooms? Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 19

EXAMPLE 6 Sketching a Graph by Using Intercepts and Symmetry Solution continued a. Find all intercepts. Set t = 0. y-intercept is 400. Set y = 0. The t-intercepts are – 10 and 10. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 20

EXAMPLE 6 Sketching a Graph by Using Intercepts and Symmetry Solution continued Check for symmetry (t replaces x). Symmetry in the t-axis: replace y with –y (0, – 400) is a solution of but not of The graph is not symmetric in the t-axis. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 21

EXAMPLE 6 Sketching a Graph by Using Intercepts and Symmetry Solution continued Symmetry in the y-axis: replace t with –t This is the original equation. Thus, (–t, y) also satisfies the equation and the graph is symmetric in the y-axis. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 22

EXAMPLE 6 Sketching a Graph by Using Intercepts and Symmetry Solution continued Symmetry in the origin: replace t with –t and y with –y (0, 400) is a solution but (– 0, – 400) is not a solution, the graph is not symmetric with respect to the origin. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 23
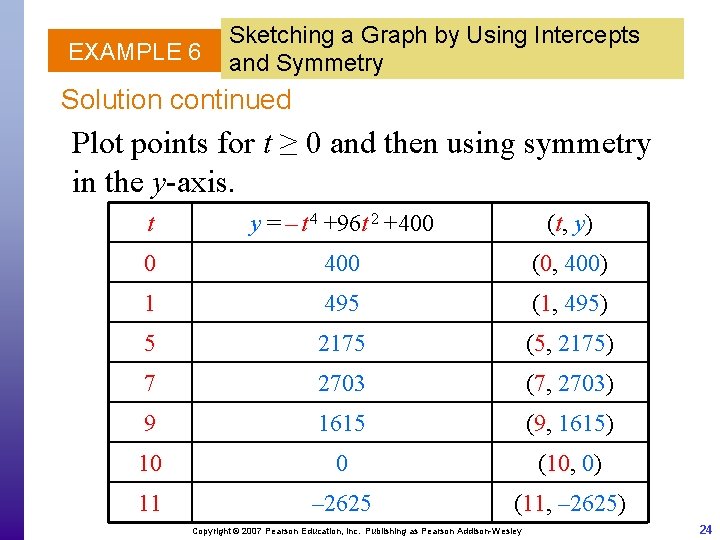
EXAMPLE 6 Sketching a Graph by Using Intercepts and Symmetry Solution continued Plot points for t ≥ 0 and then using symmetry in the y-axis. t y = – t 4 +96 t 2 +400 (t, y) 0 400 (0, 400) 1 495 (1, 495) 5 2175 (5, 2175) 7 2703 (7, 2703) 9 1615 (9, 1615) 10 0 (10, 0) 11 – 2625 (11, – 2625) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 24
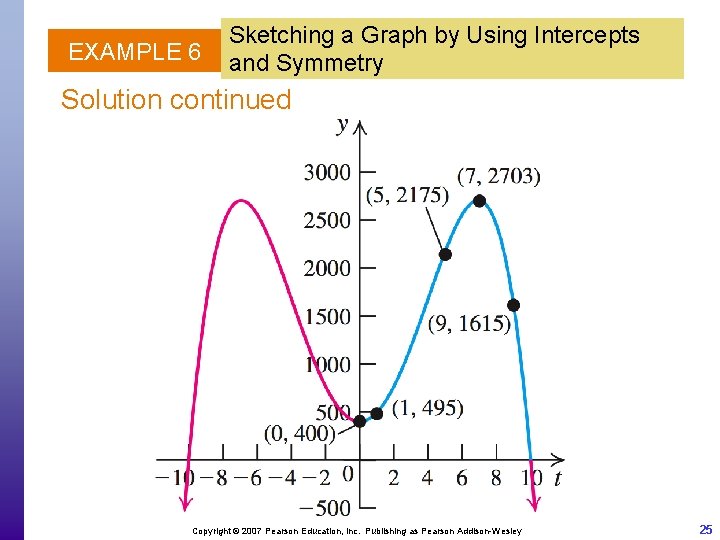
EXAMPLE 6 Sketching a Graph by Using Intercepts and Symmetry Solution continued Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 25

EXAMPLE 6 Sketching a Graph by Using Intercepts and Symmetry Solution continued b. The graph pertaining to the physical aspects of the problem is the blue portion. c. The positive t-intercept, which is 10, gives the time in years when the deer population of Dooms is 0. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 26

CIRCLE A circle is a set of points in a Cartesian coordinate plane that are at a fixed distance r from a specified point (h, k). The fixed distance r is called the radius of the circle, and the specified point (h, k) is called the center of the circle. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 27
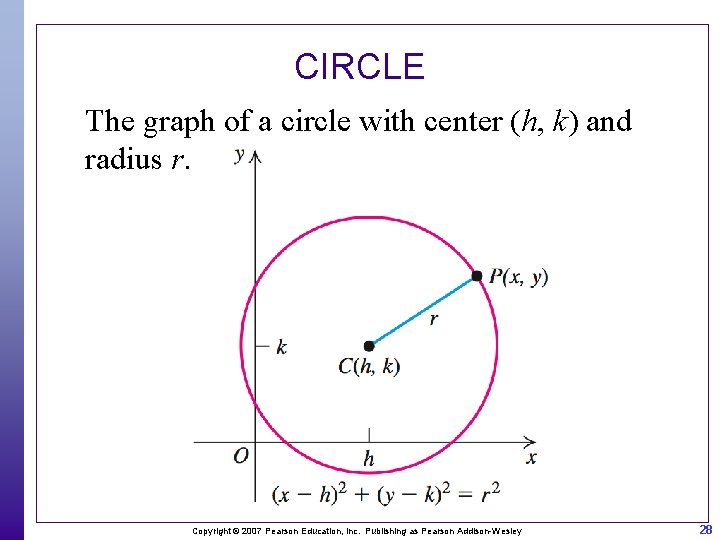
CIRCLE The graph of a circle with center (h, k) and radius r. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 28

CIRCLE The equation of a circle with center (h, k) and radius r is This equation is also called the standard form of an equation of a circle with radius r and center (h, k). Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 29

EXAMPLE 7 Finding the Equation of a Circle Find the center–radius form of the equation of the circle with center (– 3, 4) and radius 7. Solution Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 30
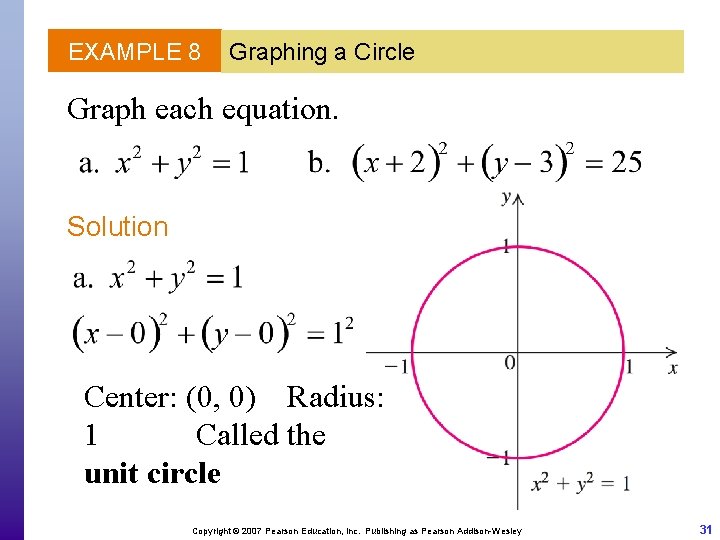
EXAMPLE 8 Graphing a Circle Graph each equation. Solution Center: (0, 0) Radius: 1 Called the unit circle Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 31
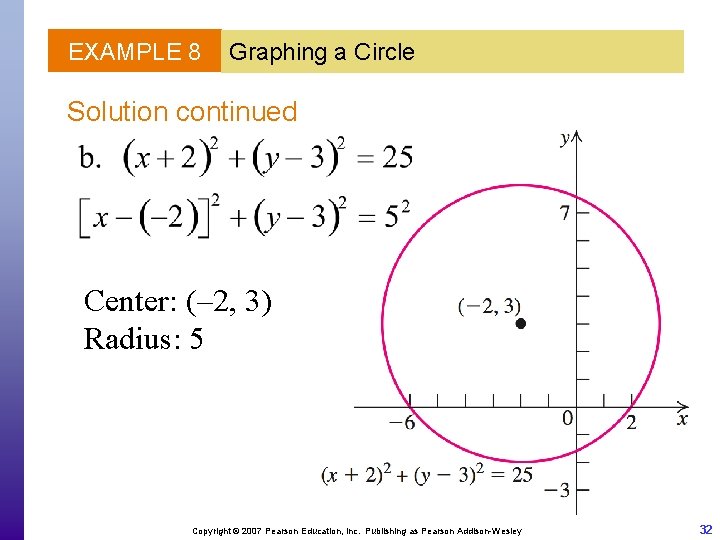
EXAMPLE 8 Graphing a Circle Solution continued Center: (– 2, 3) Radius: 5 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 32

EQUATION CIRCLE Note that stating that the equation represents the circle of radius 5 with center (– 3, 4) means two things: (i) If the values of x and y are a pair of numbers that satisfy the equation, then they are the coordinates of a point on the circle with radius 5 and center (– 3, 4). (ii) If a point is on the circle, then its coordinates satisfy the equation. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 33

GENERAL FORM OF THE EQUATION OF A CIRCLE The general form of the equation of a circle is Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 34

EXAMPLE 9 Converting the General Form to Center-Radius Form Find the center and radius of the circle with equation Solution Complete the squares on both x and y. Center: (3, – 4) Radius: Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 35
- Slides: 35