Section 2 2 Conditional Statements Rigor Identify the



















- Slides: 20

Section 2 -2: Conditional Statements Rigor: Identify the hypothesis and conclusion of a conditional statement; state truth values and counterexamples Relevance: Logical reasoning

Explore logic with Venn diagrams o Turn to page 57 Explore #1

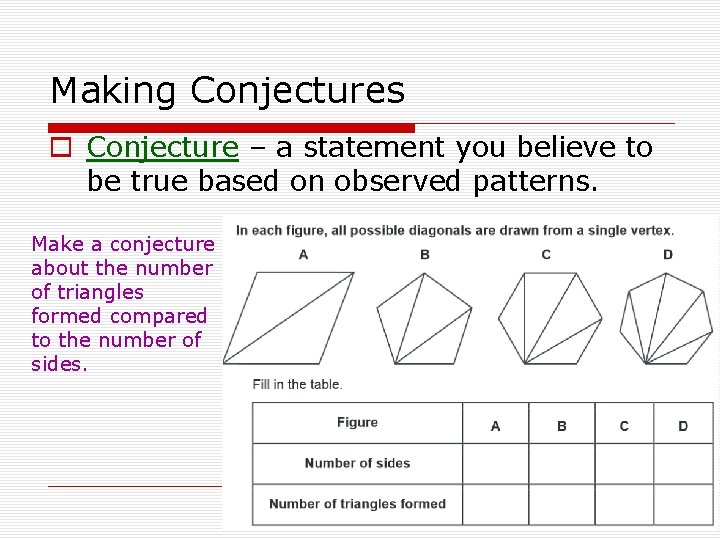
Making Conjectures o Conjecture – a statement you believe to be true based on observed patterns. Make a conjecture about the number of triangles formed compared to the number of sides.

Vocab: Conditional Statements Conditional statement – an if –then statement Hypothesis – the part p following if. Conclusion – the part q following then. p q ~P means NOT P

Identify the hypothesis and conclusion for each bumper sticker 1. If you follow me too closely, then I will flick a booger on your windshield. 2. If the rapture happens, then this car will have no driver.

Writing a conditional statement o. Step 1: Identify hypothesis and conclusion o. Step 2: Write “if…, then…” statement. Don’t forget to use a noun before the pronoun!

Example 1: Write “Vertical angles are congruent. ” as a conditional. Step 1: box hypothesis, underline conclusion Step 2:

Example 2: Write “Dolphins are mammals. ” as a conditional.

Truth Values o Conditional statements can be either TRUE or FALSE. o True Statements: If the hypothesis is true, the conclusion MUST ALWAYS be true

Counter Examples o Counter Example – an example that proves a statement is false. o You only need 1 counter example to prove a statement false!

Example: T or F? Give a counterexample for if statement is F. 1. If a woman is born in FL, then she is American. 2. If a number is divisible by 3, then it is odd.

Example: T or F? Give a counterexample for if statement is F. 3. If a month has 28 days, then it is February. 4. If two angles form a linear pair, then they are supplementary.

Video: How many examples of bad logic can you spot? http: //www. youtube. com/watch? v=zrz. M h. U_4 m-g

Another type of logic statement Converse – “If q, then p” - flip the if and then parts of a conditional statement

Example: o Conditional: o Converse: o Truth values don’t have to be the same for both logic statements!

“If I play soccer, then I’m an athlete. ” 1. What is the converse to this conditional? 2. What are the truth values of each?

“If a polygon is a square, then it is a rectangle” 1. What is the converse of the conditional statement? 2. What are the truth values of each?

“If the shape has 3 angles, then it is a triangle. ” 1. What is the converse of the conditional statement? 2. What is the truth value of each?

2 – 2 Assignment from the Workbook o pg 59 #1 – 4, 6 – 10 (do not do inverses or contrapositives) o Pg 60 # 1, 6 (do not do inverses or contrapositives) o Due Wednesday (periods 2, 4, & 6) o Due Thursday (periods 1, 5, & 7)

What is your example of a conditional statement and converse? Crazy Converses! Conditional Statement True or False? Converse True or False? Must illustrate statement and converse.