Section 2 1 Quadratic Functions and Polynomials EXAMPLE

Section 2. 1 Quadratic Functions and Polynomials

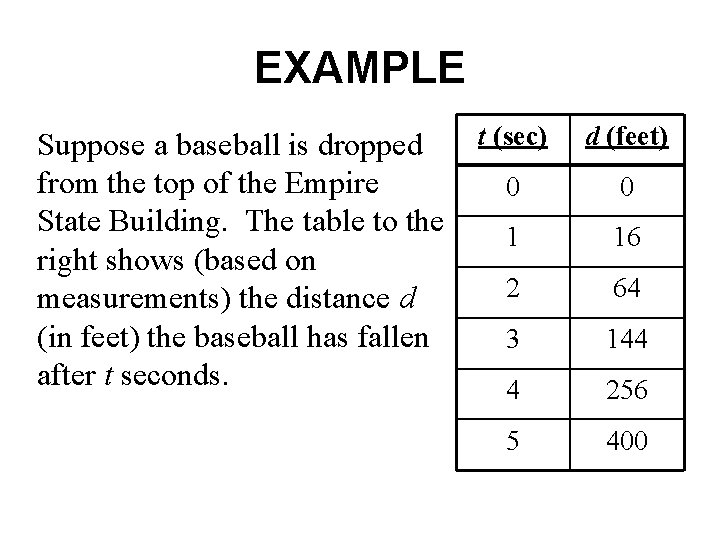
EXAMPLE Suppose a baseball is dropped from the top of the Empire State Building. The table to the right shows (based on measurements) the distance d (in feet) the baseball has fallen after t seconds. t (sec) d (feet) 0 0 1 16 2 64 3 144 4 256 5 400

A FORMULA FOR DROPPED BASEBALL Note that d is not a linear functions of t. The distance d is given by the formula d= 16 t 2. t (sec) d (feet) 0 0 1 16 2 64 3 144 4 256 5 400

QUADRATIC FUNCTIONS Definition: A quadratic function is one of the form f (x) = ax 2 + bx + c with a ≠ 0, so its formula involves a square term as well as linear and constant terms.

GRAPHS OF QUADRATIC FUNCTONS Graph the following quadratic functions on your calculator. f (x) = x 2 f (x) = -x 2 f (x) = 3 x 2 f (x) = -2 x 2 f (x) = 6 x 2 f (x) = -0. 75 x 2 f (x) = 0. 5 x 2 f (x) = x 2 – x – 6 f (x) = 0. 1 x 2 f (x) = – 2 x 2 + 3 x + 1

PARABOLAS The graph of a quadratic function is a parabola. The low point (or high point) is called the vertex. The vertex is also the place where the graph changes direction. The quadratic function f (x) = ax 2 + bx + c has its vertex at the x-value To find the y-coordinate, substitute this value in for x.

POWER FUNCTIONS Definition: A power function is one of the form f (x) = xk where k is a given constant, which can either be positive or negative, either an integer or a fraction.

GRAPHS OF POWER FUNCTIONS Graph the following power functions. f (x) = x 2 f (x) = x 1/2 f (x) = x 4 f (x) = x 3 f (x) = x 1/3 f (x) = x 6 f (x) = x 5

POLYNOMIALS Definition: A polynomial function (or simply a polynomial) is a sum of constant multiples of the power functions 1, x, x 2, x 3, . . . xn, . . . The degree of the polynomial is equals the exponent of the highest power appearing among its terms.

THE “END BEHAVIOR” OF A POLYNOMIAL The end behavior of a graph is what the shape of the graph is on the extreme left and extreme right. The end behavior of a polynomial is the same the end behavior of the term with the highest power.

TURNING POINTS OF POLYNOMIALS In general, the graph of a polynomial can have as many degree - 1 turning points (or “bends”). In other words, if the degree of the polynomial is n, the graph can have as many as n - 1 turning points (or “bends”).

SOLVING POLYNOMIAL EQUATIONS Principle: Graphic Solution of Equations The solutions of the equation f (x) = 0 are precisely the x-intercepts of the graph y = f (x). Recall, x-intercepts are the places where the graph crosses (or touches) the x-axis.