Section 2 1 Proof Techniques Introduce proof techniques








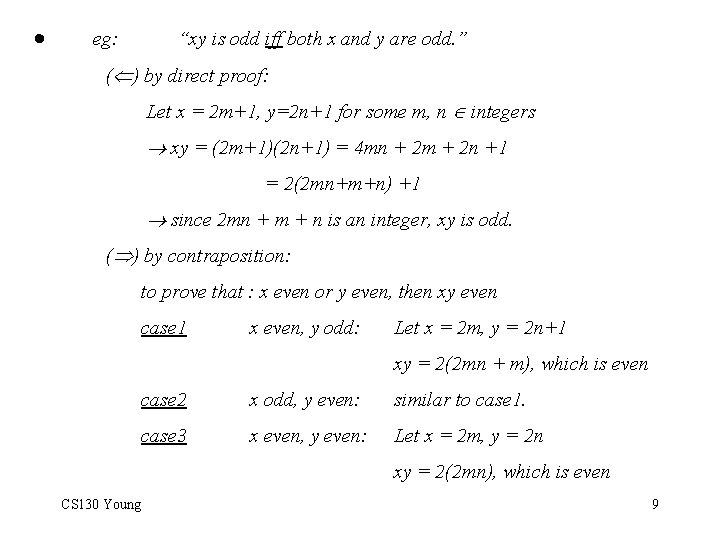


- Slides: 11

Section 2. 1 Proof Techniques Introduce proof techniques: o Exhaustive Proof: to prove all possible cases, Only if it is about a finite collection o Direct Proof: to prove P Q is true, Assume P is true, and deduce Q. (like what we have done in Chap 1) o Contraposition: to prove P Q is true By proving Q P CS 130 Young 1

o Contradiction: (indirect proof) to prove P Q is true, Assume both the hypothesis and the negation of the conclusion are true, then try to deduce some contradiction from this assumption. o Counterexample: to disprove something o Induction: to prove that P(n) is true, n Use the principle of mathematical induction: P(1) is true k[ P(k) true P(k+1) true] CS 130 Young P(n) true, n 2

· Proof by Exhaustion: eg: “For any positive integer n less than or equal to 3, n! < 2 n” CS 130 Young n n! 2 n 1 1 2 2 2 4 3 6 8 3

eg: “If an integer between 5 and 15 is divisible by 6, then it is also divisible by 3” Number Divisible by 6 Divisible by 3 5 No No 6 Yes: 6 = 1 X 6 Yes: 6 = 2 X 3 7 No No 8 No No 9 No Yes 10 No No 11 No No 12 Yes: 12 = 2 X 6 Yes: 12 = 4 X 3 13 No No 14 No No 15 No Yes (Note: If the above problem is about all integers, then we cannot use exhaustive proof) CS 130 Young 4

Proof by Counterexample: eg: “Every integer less than 10 is bigger than 5” To prove the statement is not true, find a counterexample, integer = 4 < 10, but not > 5. eg: disprove that “the sum of any three consecutive integers is even. ” counterexample : 2+3+4=9 CS 130 Young 5

· Direct Proof: eg: “for all x [x is divisible by 6 x is divisible by 3]” X is divisible by 6 x = k*6, for some integer k (hypothesis) x = k*2*3 x = (k*2)*3 (k*2) is some integer CS 130 Young x is divisible by 3 6

eg: “the product of two even integers is even” Let x = 2 m, y = 2 n for some integer m, n (hypothesis) xy = (2 m)(2 n) = 2(2 mn), which is even. eg: “the sum of two odd integers is even” Let x = 2 m+1, y = 2 n+1 for some integer m, n (hypothesis) x + y = 2 m + 2 n+ 2 = 2(m+n+1), where m+n+1 is an integer x+y is even. CS 130 Young 7

· Contraposition: eg: “If the square of an integer is odd, then the integer must be odd. ” “n 2 odd n odd” Prove: n even n 2 even (P Q Q P ) Let n = 2 m for some integer m (hypothesis) n 2 = n * n = 2 m*2 m = 2(2 m 2) n 2 is even. CS 130 Young 8
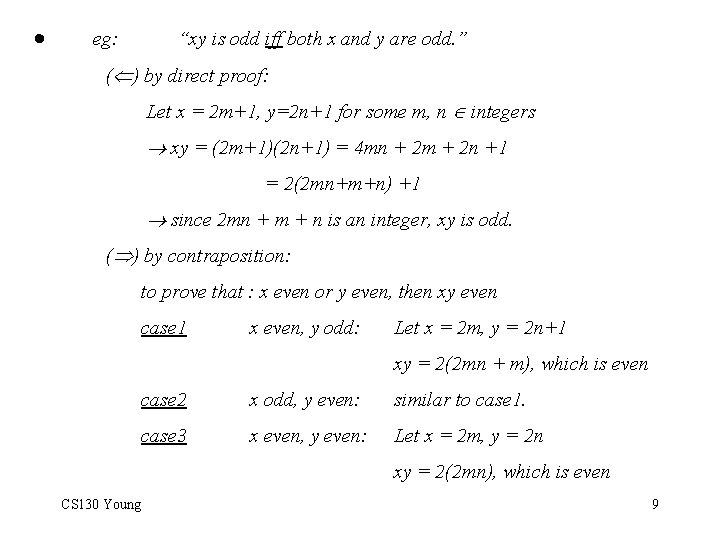
· eg: “xy is odd iff both x and y are odd. ” ( ) by direct proof: Let x = 2 m+1, y=2 n+1 for some m, n integers xy = (2 m+1)(2 n+1) = 4 mn + 2 m + 2 n +1 = 2(2 mn+m+n) +1 since 2 mn + m + n is an integer, xy is odd. ( ) by contraposition: to prove that : x even or y even, then xy even case 1 x even, y odd: Let x = 2 m, y = 2 n+1 xy = 2(2 mn + m), which is even case 2 x odd, y even: similar to case 1. case 3 x even, y even: Let x = 2 m, y = 2 n xy = 2(2 mn), which is even CS 130 Young 9

· Proof by Contradiction: Since (P Q F) (P Q) is a tautology, It is sufficient to prove P Q F, then P Q is true. eg: “If a number added to itself gives itself, then the number is 0. ” i. e. “x + x = x, then x = 0”: Assume x + x = x and x 0 2 = 1, which is a contradiction CS 130 Young the assumption must be wrong 10

·eg: “if x 2 + 2 x – 3 = 0, then x 2” Let x 2 + 2 x – 3 = 0 and assume x = 2, 4 + 4 – 3 = 0 or 5 = 0, which is a contradiction. ( by direct proof: if x 2 + 2 x – 3 = 0 (x + 3)(x – 1)= 0 x = -3 or x = 1 x 2 (by contraposition: CS 130 Young ) if x = 2 x 2 + 2 x – 3 = 5 0 ) 11