Section 2 1 Classwork 1 TANGENT LINE Slope

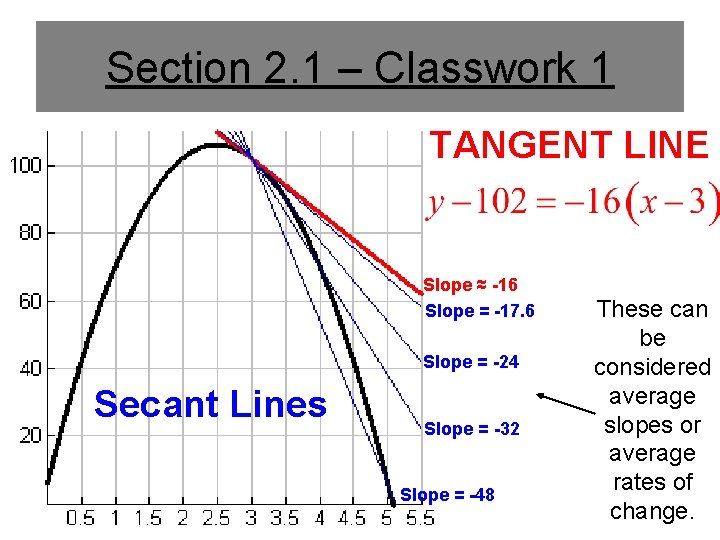
Section 2. 1 – Classwork 1 TANGENT LINE Slope ≈ -16 Slope = -17. 6 Slope = -24 Secant Lines Slope = -32 Slope = -48 These can be considered average slopes or average rates of change.

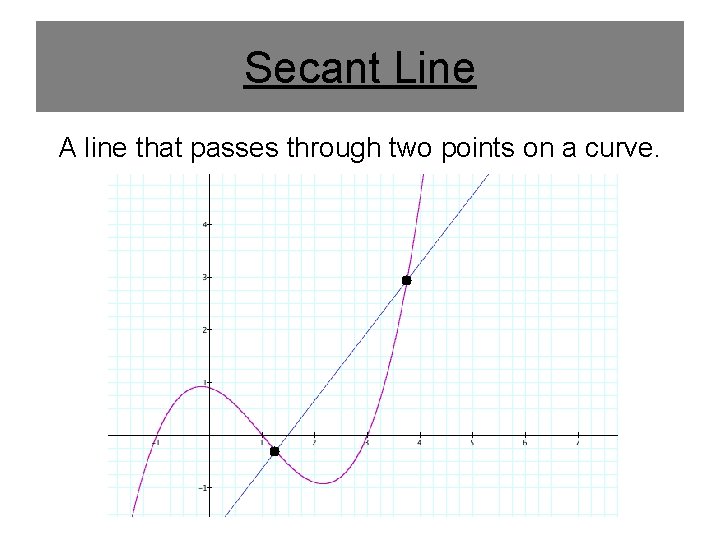
Secant Line A line that passes through two points on a curve.

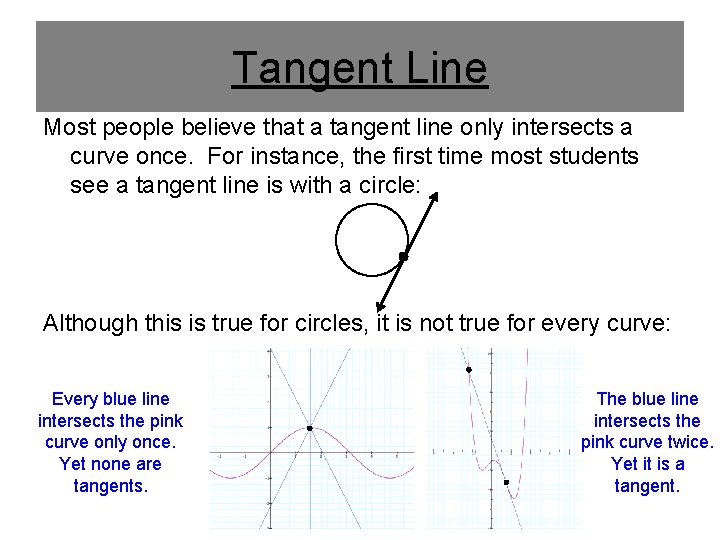
Tangent Line Most people believe that a tangent line only intersects a curve once. For instance, the first time most students see a tangent line is with a circle: Although this is true for circles, it is not true for every curve: Every blue line intersects the pink curve only once. Yet none are tangents. The blue line intersects the pink curve twice. Yet it is a tangent.

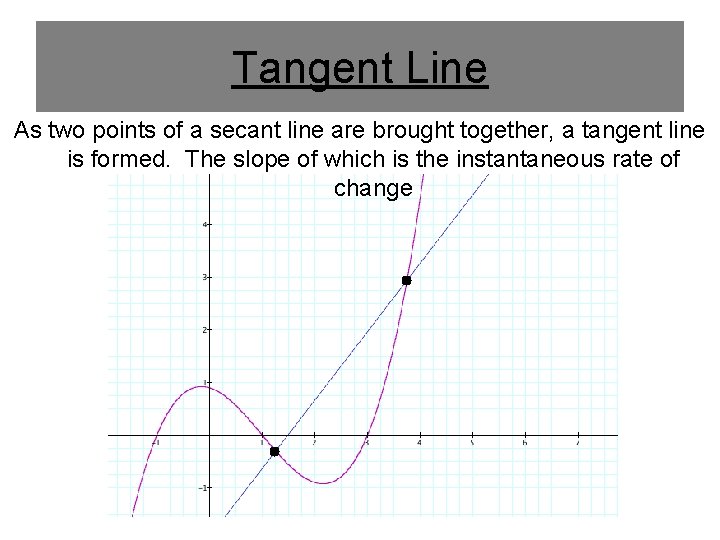
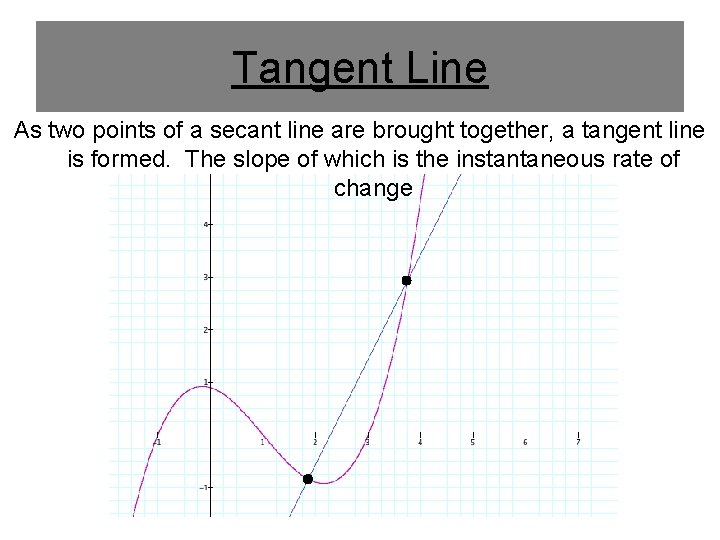
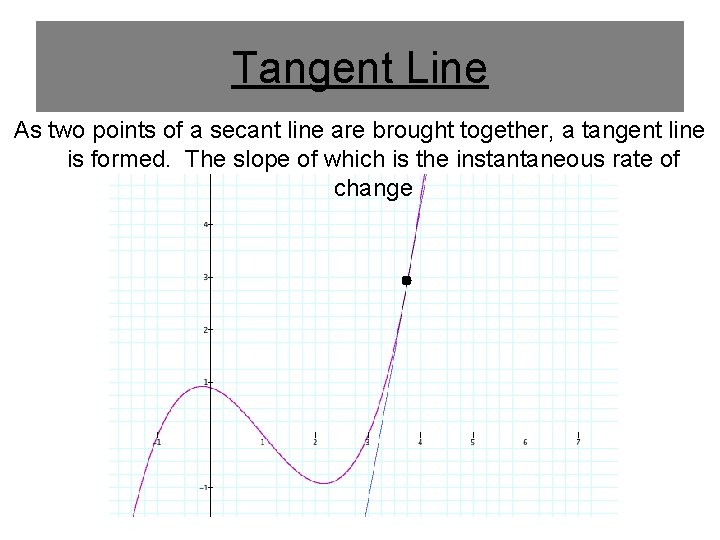
Tangent Line As two points of a secant line are brought together, a tangent line is formed. The slope of which is the instantaneous rate of change

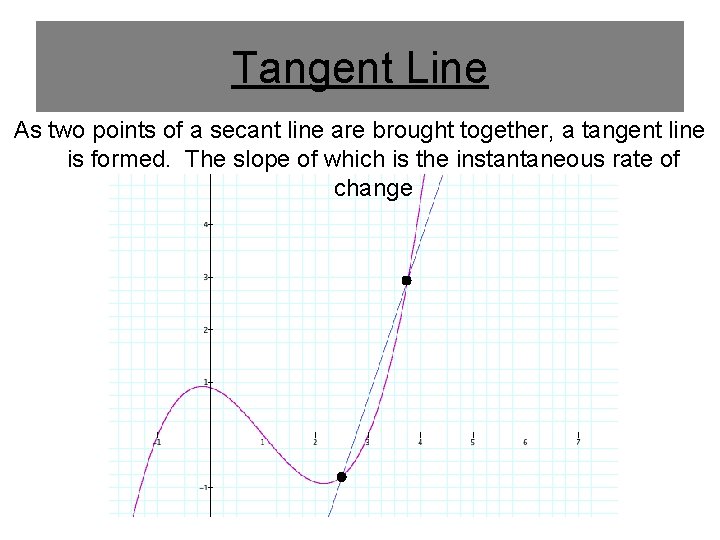
Tangent Line As two points of a secant line are brought together, a tangent line is formed. The slope of which is the instantaneous rate of change

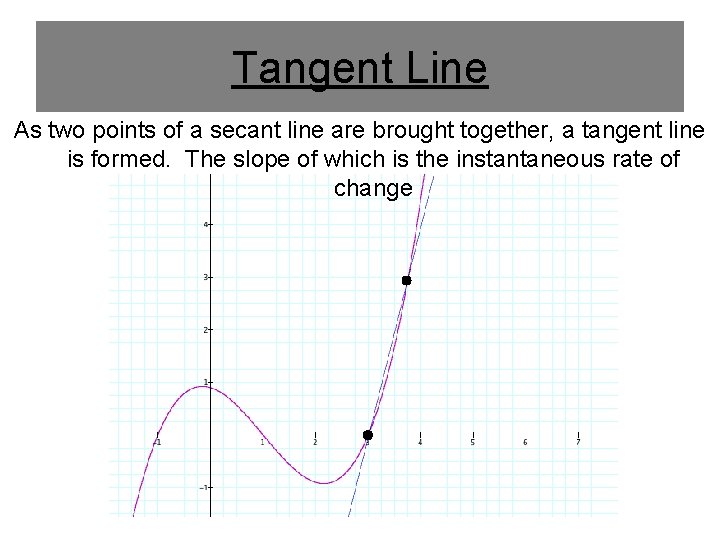
Tangent Line As two points of a secant line are brought together, a tangent line is formed. The slope of which is the instantaneous rate of change

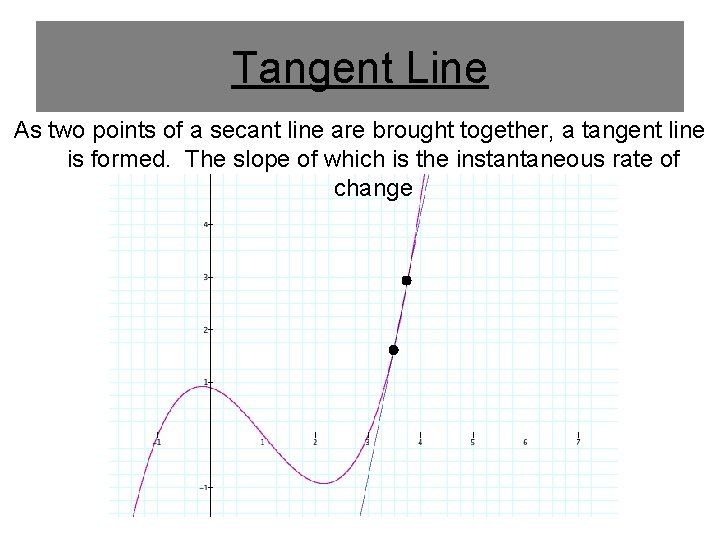
Tangent Line As two points of a secant line are brought together, a tangent line is formed. The slope of which is the instantaneous rate of change

Tangent Line As two points of a secant line are brought together, a tangent line is formed. The slope of which is the instantaneous rate of change

Tangent Line As two points of a secant line are brought together, a tangent line is formed. The slope of which is the instantaneous rate of change

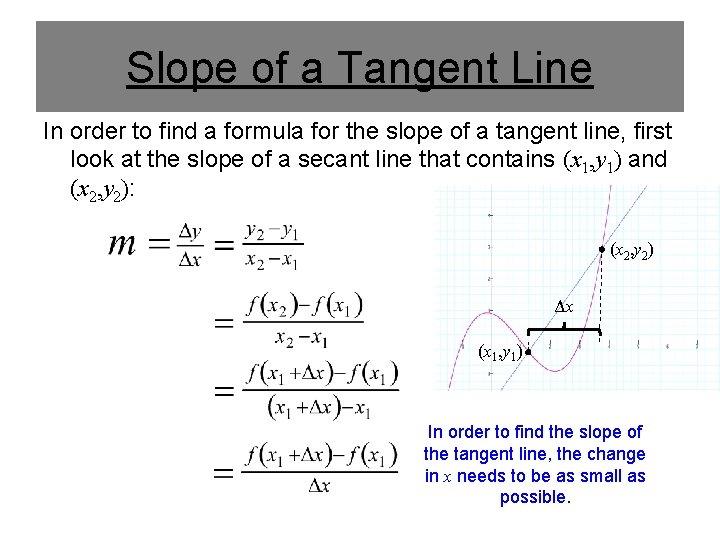
Slope of a Tangent Line In order to find a formula for the slope of a tangent line, first look at the slope of a secant line that contains (x 1, y 1) and (x 2, y 2): (x 2, y 2) Δx (x 1, y 1) In order to find the slope of the tangent line, the change in x needs to be as small as possible.

Instantaneous Rate of Change Tangent Line with Slope m If f is defined on an open interval containing c, and if the limit exists, then the line passing through (c, f(c)) with slope m is the tangent line to the graph of f at the point (c, f(c)). f(x) m (c, f(c))

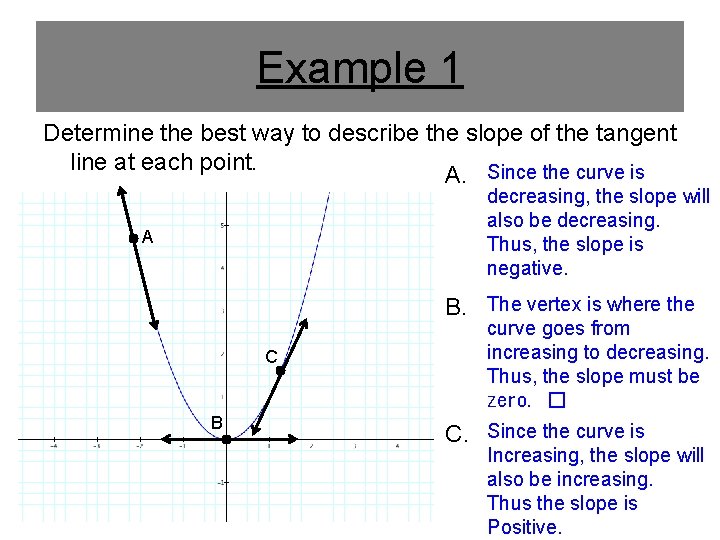
Example 1 Determine the best way to describe the slope of the tangent line at each point. A. Since the curve is decreasing, the slope will also be decreasing. Thus, the slope is negative. A B. The vertex is where the C B curve goes from increasing to decreasing. Thus, the slope must be zero. � C. Since the curve is Increasing, the slope will also be increasing. Thus the slope is Positive.

Example 2 Find the instantaneous rate of change to at (3, -6). Substitute into the function c is the x-coordinate of the point on the curve Simplify in order to cancel the denominator Direct substitution

Example 3 Find the equation of the tangent line to at (2, 10). Substitute into the function c is the x-coordinate of the point on the curve Just the slope. Now use the point-slope formula to find the equation Simplify in order to cancel the denominator Direct substitution

A Function to Describe Slope In the preceding notes, we considered the slope of a tangent line of a function f at a number c. Now, we change our point of view and let the number c vary by replacing it with x. A constant. variable. A function whose The slope of a output is theline slope of a tangent at the tangentpoint line xat=any c. x.

Example Derive a formula for the slope of the tangent line to the graph of . Multiply by a common denominator Substitute into the function A formula to find the slope of any tangent line at x. Simplify in order to cancel the denominator Direct substitution

The Derivative of a Function The limit used to define the slope of a tangent line is also used to define of the two fundamental operations of calculus: The derivative of f at x is given by READ: “f prime of x. ” Provided the limit exists. For all x for which this limit exists, f’ is a function of x. Other Notations for a Derivative:

Example 1 Differentiate . Simplify in order to cancel the denominator Substitute into the function Direct substitution Make the problem easier by factoring out common constants

Example 2 Find the tangent line equation(s) for such that the tangent line has a slope of 12. Find when the derivative equals 12 Find the derivative first since the derivative finds the slope for an x value Find the output of the function for every input Use the point-slope formula to find the equations

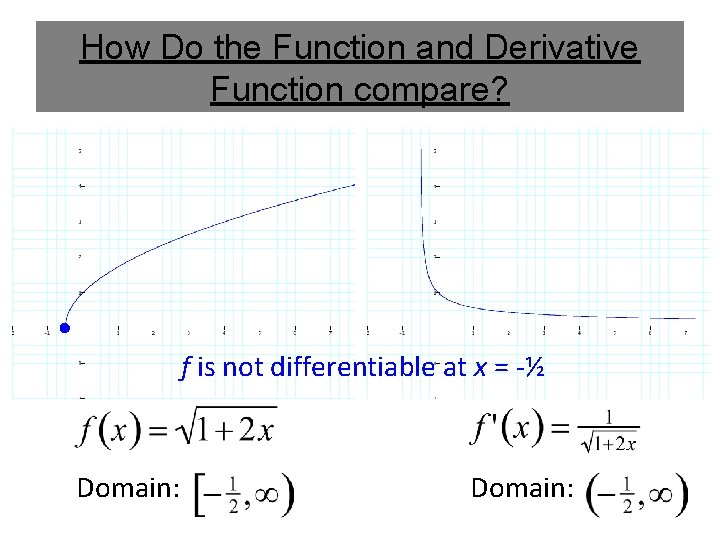
How Do the Function and Derivative Function compare? f is not differentiable at x = -½ Domain:

Differentiability Justification 1 In order to prove that a function is differentiable at x = c, you must show the following: In other words, the derivative from the left side MUST EQUAL the derivative from the right side. Common Example of a way for a derivative to fail: Not differentiable at x = -4 Other common examples: Corners or Cusps

Differentiability Justification 2 In order to prove that a function is differentiable at x = c, you must show the following: In other words, the function must be continuous. Common Example of a way for a derivative to fail: Not differentiable at x = 0 Other common examples: Gaps, Jumps, Asymptotes

Differentiability Justification 3 In order to prove that a function is differentiable at x = c, you must show the following: In other words, the tangent line can not be a vertical line. An Example of a Vertical tangent where the derivative to Fails to exist: Not differentiable at x = 0

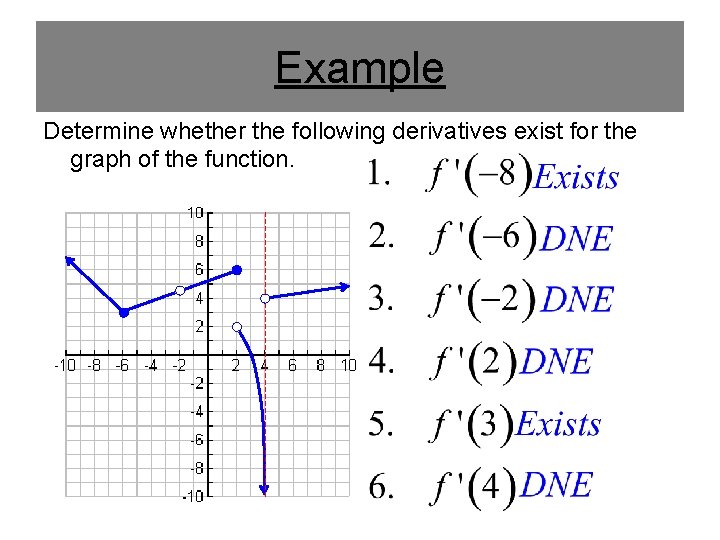
Example Determine whether the following derivatives exist for the graph of the function.

Example 2 Sketch a graph of the function with the following characteristics: The derivative does not exist at x = -2. The function is continuous on (-6, 3) The Range is (-7, -1]

Example 3 Show that does not exist if . First rewrite the absolute value function as a piecewise function Find the Left Hand Derivative Find the Right Hand Derivative Since the one-sided limits are not equal, the derivative does not exist

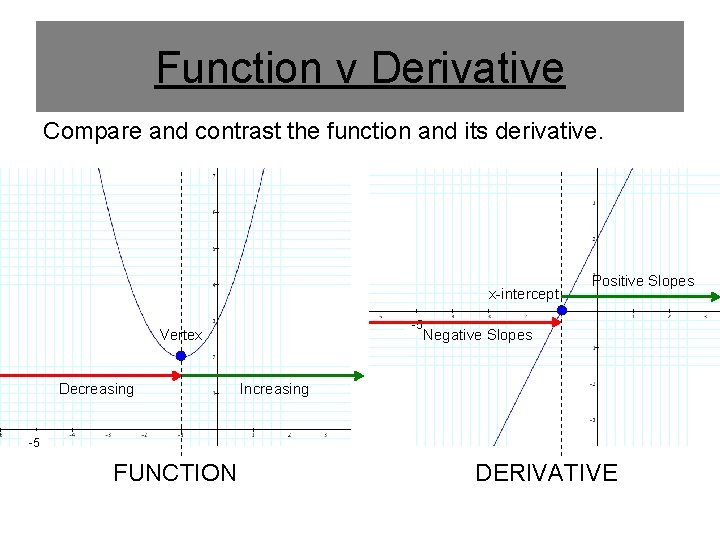
Function v Derivative Compare and contrast the function and its derivative. x-intercept -5 Vertex Decreasing Positive Slopes Negative Slopes Increasing -5 FUNCTION DERIVATIVE

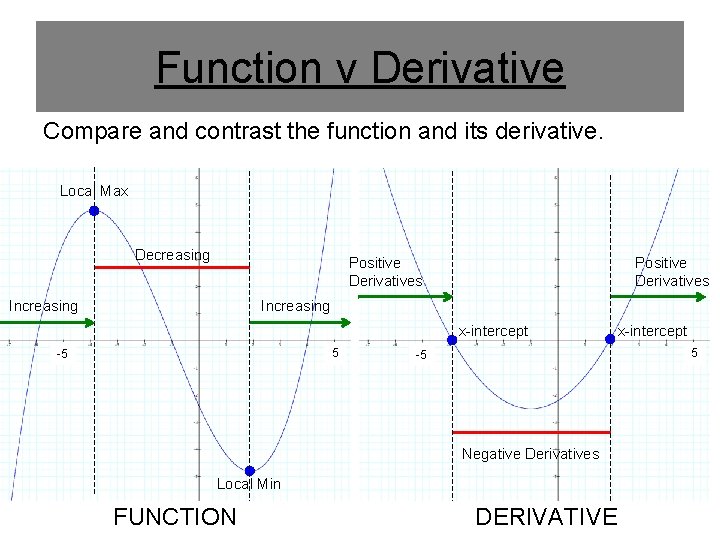
Function v Derivative Compare and contrast the function and its derivative. Local Max Decreasing Positive Derivatives Increasing x-intercept 5 -5 Negative Derivatives Local Min FUNCTION DERIVATIVE

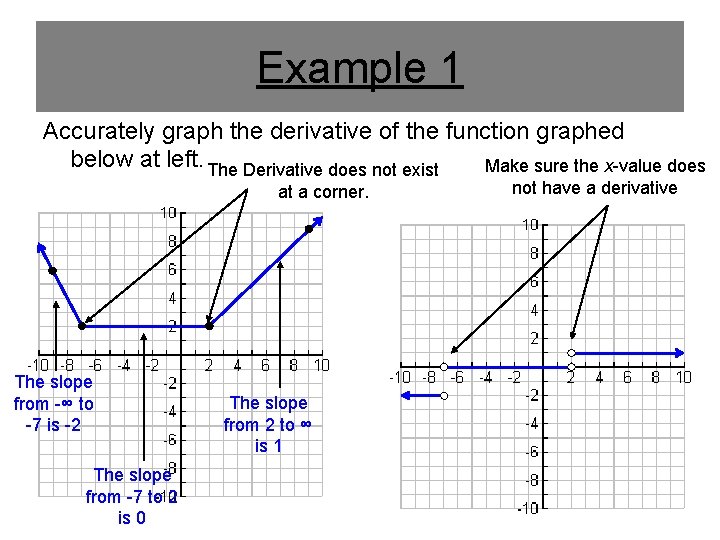
Example 1 Accurately graph the derivative of the function graphed below at left. The Derivative does not exist Make sure the x-value does at a corner. The slope from -∞ to -7 is -2 The slope from -7 to 2 is 0 The slope from 2 to ∞ is 1 not have a derivative

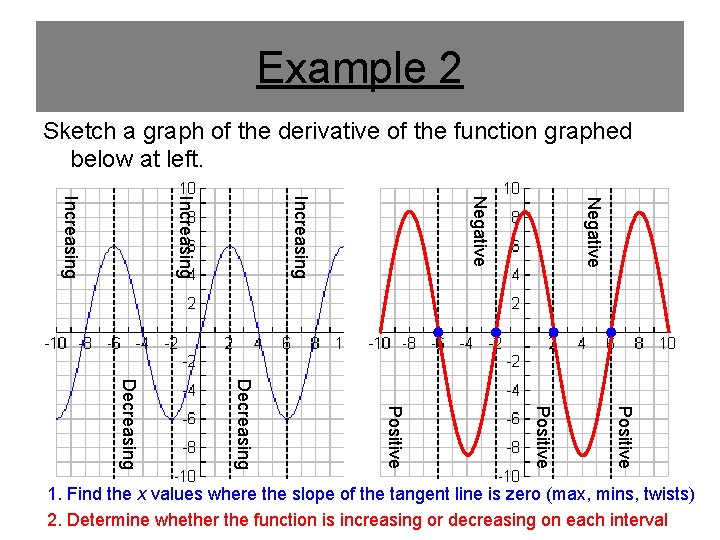
Example 2 Sketch a graph of the derivative of the function graphed below at left. Negative Increasing Positive Decreasing 1. Find the x values where the slope of the tangent line is zero (max, mins, twists) 2. Determine whether the function is increasing or decreasing on each interval

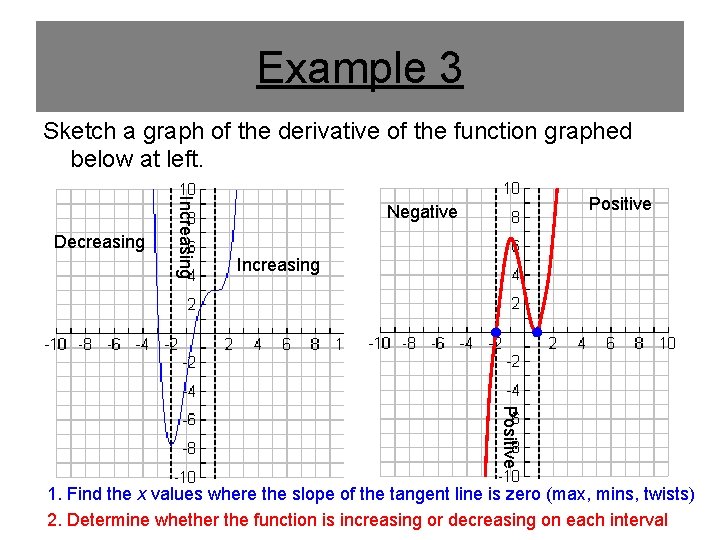
Example 3 Sketch a graph of the derivative of the function graphed below at left. Increasing Decreasing Positive Negative Increasing Positive 1. Find the x values where the slope of the tangent line is zero (max, mins, twists) 2. Determine whether the function is increasing or decreasing on each interval

Example 4 Sketch a graph of the derivative of the function graphed below. (-3, 0) (-2. 2, -4) (0, 0) (2. 2, -4) (3, 0)

Example 5 Sketch a graph of the function with the following characteristics: The derivative is only positive for -6<x<-3 and 5<x<10. The function is differentiable on (-6, 10)

Differentiability Implies Continuity If f is differentiable at x = c, then f is continuous at x = c. The contrapositive of this statement is true: If f is NOT continuous at x = c, then f is NOT differentiable at x = c. The converse of this statement is not always true (be careful): If f is continuous at x = c, then f is differentiable at x = c. The inverse of this statement is not always true: If f is NOT differentiable at x = c, then f is NOT continuous at x = c.

Example Sketch a graph of the function with the following characteristics: The derivative does NOT exist at x = -2. The derivative equals 0 at x = 1. The derivative does NOT exist at x = 4. The function is continuous on [-4, -2)U(-2, 5]