Section 16 7 Triple Integrals TRIPLE INTEGRAL OVER

Section 16. 7 Triple Integrals

TRIPLE INTEGRAL OVER A BOX Consider a function w = f (x, y, z) of three variables defined on the box B given by Divide B into sub-boxes by dividing the interval [a, b] into l subintervals of equal width Δx, dividing [c, d] into m subintervals of equal width Δy, and dividing [r, s] into n subintervals of equal width Δz. This divides the box B into l∙m∙n sub-boxes. A typical sub-box Bilk is Bijk = [xi − 1, xi] × [yj − 1, yj] × [zk − 1, zk] Each sub-box has volume ΔV = Δx Δy Δz.

TRIPLE INTEGRAL OVER A BOX (CONTINUED) We now form the triple Riemann sum where the sample point Bijk. is in box

TRIPLE INTEGRAL OVER A BOX (CONCLUDED) The triple integral of f over the box B is if this limit exists. The triple integral always exists if f is continuous. If we choose the sample point to be (xi, yj, zk), the triple integral simplifies to

FUBINI’S THEOREM FOR TRIPLE INTEGRAL Theorem: If f is continuous on the rectangular box B = [a, b] × [c, d] × [r, s], then NOTE: The order of the partial antiderivatives does not matter as long as the endpoints correspond to the proper variable.

EXAMPLE Evaluate the triple integral , where B is the rectangular box given by B = {(x, y, z) | 1 ≤ x ≤ 2, 0 ≤ y ≤ 1, 0 ≤ z ≤ 2}

TRIPLE INTEGRAL OVER A BOUNDED REGION The triple integral over the bounded region E is defined as where B is a box containing the region E and the function F is defined as

TYPE 1 REGIONS The region E is said to by of type 1 if it lies between to continuous functions of x and y. That is, where D is the projection of E onto the xy-plane. The triple integral over a type 1 region is

TYPE 1 REGIONS (CONTINUED) If D is a type I region in the xy-plane, then E can be described as and the triple integral becomes

TYPE 1 REGIONS (CONCLUDED) If D is a type II region in the xy-plane, then E can be described as and the triple integral becomes

EXAMPLE Evaluate the triple integral , where E is the region bounded by the planes x = 0, y = 0, z = 0, and 2 x + 2 y + z = 4.

TYPE 2 REGIONS The region E is said to by of type 2 if it lies between two continuous functions of y and z. That is, where D is the projection of E onto the yz-plane. The triple integral over a type 2 region is

TYPE 3 REGIONS The region E is said to by of type 3 if it lies between two continuous functions of x and z. That is, where D is the projection of E onto the xz-plane. The triple integral over a type 3 region is

EXAMPLE Evaluate the triple integral , where E is the region bounded by the paraboloid x = y 2 + z 2 and the plane x = 4.

VOLUME AND TRIPLE INTEGRALS The triple integral of the function f (x, y, z) = 1 over the region E gives the volume of E; that is,

EXAMPLE Find the volume of the region E bounded by the plane z = 0, the plane z = x, and the cylinder x = 4 − y 2.

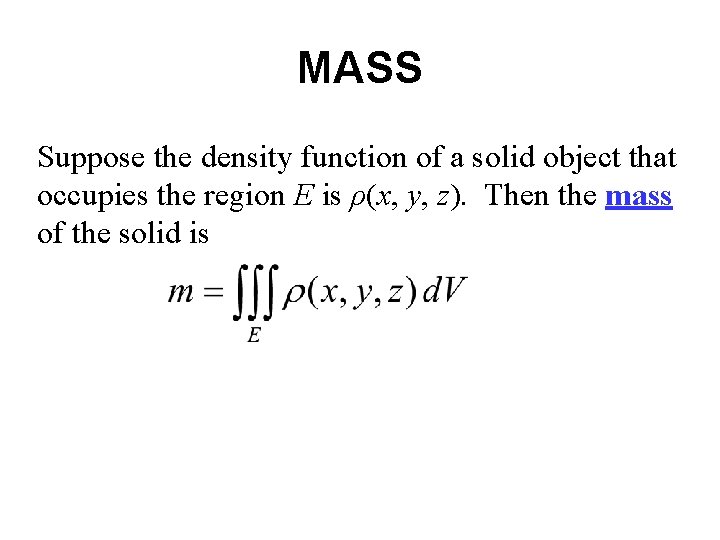
MASS Suppose the density function of a solid object that occupies the region E is ρ(x, y, z). Then the mass of the solid is

MOMENTS Suppose the density function of a solid object that occupies the region E is ρ(x, y, z). Then the moments of the solid about the three coordinate planes are

CENTER OF MASS The center of mass is located at the point where If the density is constant, the center of mass of the solid is called the centroid of E.

MOMENTS OF INERTIA The moments of inertia about the three coordinate axis are

EXAMPLE Find the mass and center of mass of the tetrahedron bounded by the planes x = 0, y = 0, z = 0, and x + y + z = 1 whose density function is given by ρ(x, y, z) = y.