Section 14 4 Trees Copyright 2013 2010 2007



















- Slides: 22

Section 14. 4 Trees Copyright 2013, 2010, 2007, Pearson, Education, Inc.

What You Will Learn Trees Spanning Trees Kruskal’s Algorithm 14. 4 -2 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Tree A tree is a connected graph in which each edge is a bridge. 14. 4 -3 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Examples Trees 14. 4 -4 Not Trees Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Spanning Tree A spanning tree is a tree that is created from another graph by removing edges while still maintaining a path to each vertex. 14. 4 -5 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 3: A Spanning Tree Problem Schoolcraft College is considering adding awnings above its sidewalks to help shelter students from the snow and rain while they walk between some of the buildings on campus. A diagram of the buildings and the connecting sidewalks where the awnings are to be added is on the next slide. 14. 4 -6 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

14. 4 -7 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 3: A Spanning Tree Problem Originally, the president of the college wished to have awnings placed over all the sidewalks shown, but that was found to be too costly. Instead, the president has proposed to place just enough awnings over a select number of sidewalks so that, by moving from building to building, students would still 14. 4 -8 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 3: A Spanning Tree Problem be able to reach any location shown without being exposed to the elements. a) Represent all the buildings and sidewalks shown with a graph. b) Create three different spanning trees from this graph that would satisfy the president’s proposal. 14. 4 -9 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 3: A Spanning Tree Problem Solution a) Using letters to represent the building names, vertices to represent the buildings, and edges to represent the sidewalks between buildings, we generate this graph. 14. 4 -10 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

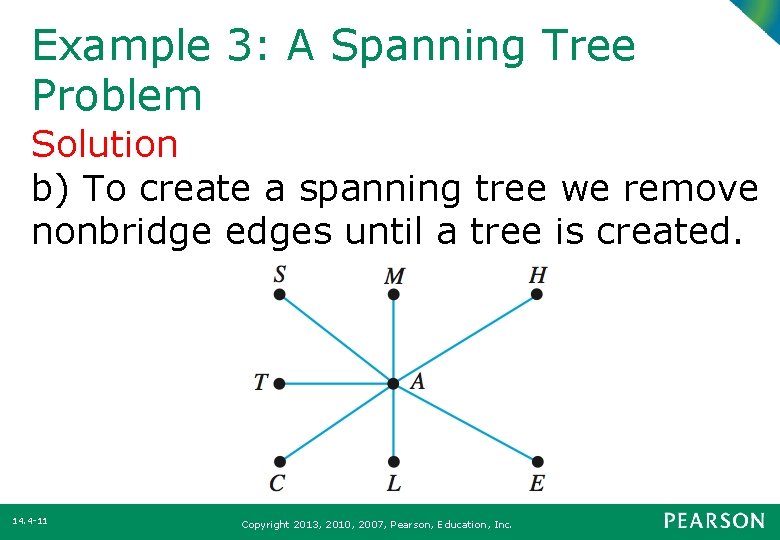
Example 3: A Spanning Tree Problem Solution b) To create a spanning tree we remove nonbridge edges until a tree is created. 14. 4 -11 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

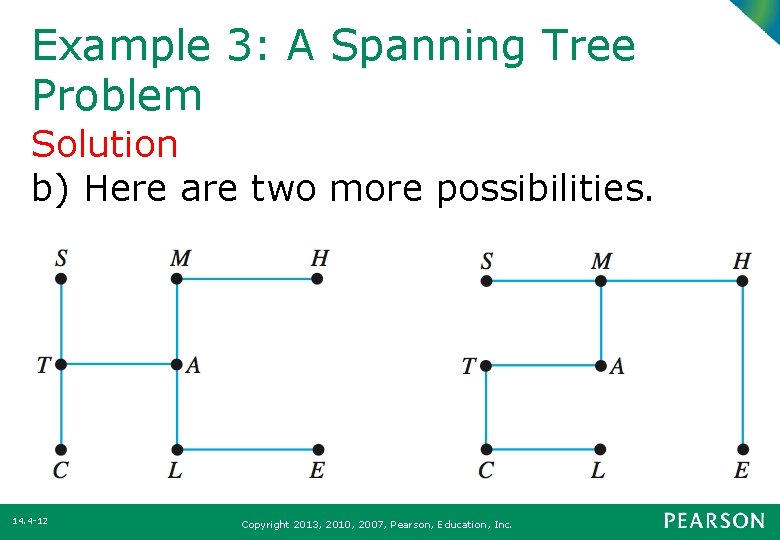
Example 3: A Spanning Tree Problem Solution b) Here are two more possibilities. 14. 4 -12 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Minimum-cost spanning tree A minimum cost spanning tree is the least expensive spanning tree of all spanning trees under consideration. 14. 4 -13 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Kruskal’s Algorithm To construct the minimum-cost spanning tree from a weighted graph: 1. Select the lowest-cost edge on the graph. 2. Select the next lowest-cost edge that does not form a circuit with the first edge. 3. Select the next lowest-cost edge that does not form a circuit with the previously selected edges. 14. 4 -14 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Kruskal’s Algorithm 4. Continue selecting the lowest-cost edges that do not form circuits with the previously selected edges. 5. When a spanning tree is complete, you have the minimum-cost spanning tree. 14. 4 -15 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 7 Schools in Budville, Fairplay, Happy Corners, Kieler, Louisburg, and Sinsinawa, Wisconsin, all wish to establish a fiber-optic computer network to share information and to obtain Internet access. The most efficient method of establishing such a network would be to install fiber-optic cable along roadsides. 14. 4 -16 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

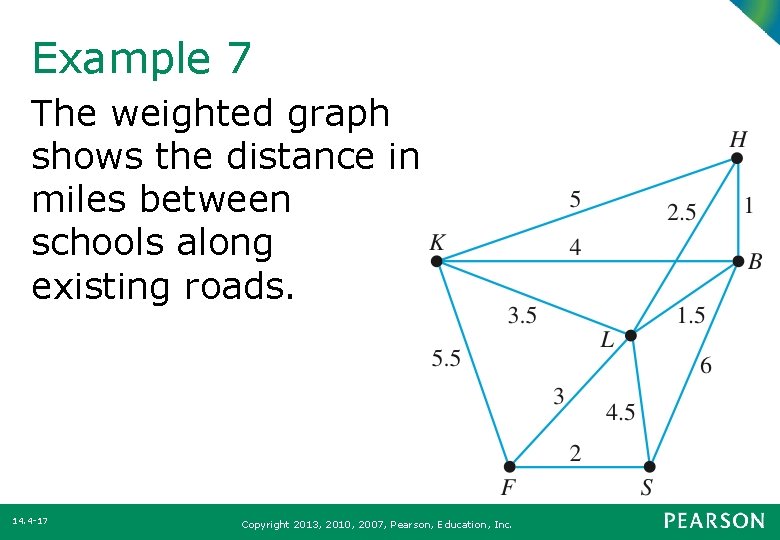
Example 7 The weighted graph shows the distance in miles between schools along existing roads. 14. 4 -17 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 7 a) Determine the shortest distance to link these six schools. b) The cost to install fiber-optic cable is $1257 per mile. What is the minimum cost to install the fiberoptic cable along the roadsides determined in part (a)? 14. 4 -18 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 7 Solution a) We are seeking the minimum-cost spanning tree. Use Kruskal’s algorithm. Select edge HB, 1 mi; edge BL, 1. 5 mi; edge FS, 2 mi 14. 4 -19 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 7 Solution Selecting HL, 2. 5 mi creates a circuit between H, B, L; so we must select LF, 3 mi. Finally, select edge KL, 3. 5 mi. 14. 4 -20 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 7 Solution According to Kruskal’s algorithm, this figure shows the minimum-cost spanning tree. Place the fiber-optic cable along this path. 14. 4 -21 Copyright 2013, 2010, 2007, Pearson, Education, Inc.

Example 7 Solution b) From the figure, there are 1 + 1. 5 + 3 + 2 = 11 miles of fiber-optic cable needed. At $1257 per mile, the cost is $1257 × 11 = $13, 827. 14. 4 -22 Copyright 2013, 2010, 2007, Pearson, Education, Inc.