Section 14 3 Apportionment Methods Objectives 1 2

Section 14. 3 Apportionment Methods Objectives 1. 2. 3. 4. 5. 6. 7. Find standard divisors and standard quotas. Understand the apportionment problem. Use Hamilton’s method. Understand the quota rule. Use Jefferson’s method. Use Adam’s method. Use Webster’s method. 2/13/2022 Section 14. 3 1

Standard Divisors and Standard Quotas Standard Divisors The standard divisor is found by dividing the total population under consideration by the number of items to be allocated. Standard divisor = total population number of allocated items Example: The Republic of Margaritaville is composed of four states, A, B, C, and D. The table of each state’s population (in thousands) is given below. 2/13/2022 State A B C D Total Population 275 383 465 767 1890 Section 14. 3 2

Standard Divisors and Standard Quotas Standard Divisors Example Continued According to the country’s constitution, the congress will have 30 seats. So, the standard divisor for the population of Margaritaville is Thus, there are 63 thousand people for each seat in congress. 2/13/2022 Section 14. 3 3

Standard Divisors and Standard Quotas The standard quota for a particular group is found by dividing that group’s population by the standard divisor. Standard quota = population of a particular group standard divisor Example: Find the standard quotas for states A, B, C, and D in Margaritaville. Solution: The standard quotas are obtained by dividing each state’s population by the standard divisor 63 in which we obtained in the previous example. 2/13/2022 Section 14. 3 4

Standard Divisors and Standard Quotas Example Continued • Standard quota for state A = population of state A standard divisor = 275 / 63 ≈ 4. 37 • Standard quota for state B = population of state B standard divisor = 383 / 63 ≈ 6. 08 2/13/2022 Section 14. 3 5

Standard Divisors and Standard Quotas Example Continued • Standard quota for state C = population of state C standard divisor = 465 / 63 ≈ 7. 38 • Standard quota for state D = population of state D standard divisor = 767 / 63 ≈ 12. 17 2/13/2022 Section 14. 3 6

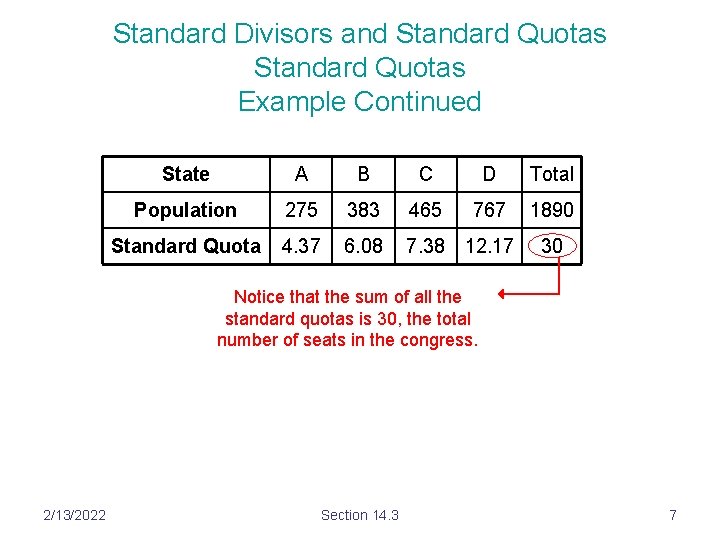
Standard Divisors and Standard Quotas Example Continued State A B C D Total Population 275 383 465 767 1890 Standard Quota 4. 37 6. 08 7. 38 12. 17 30 Notice that the sum of all the standard quotas is 30, the total number of seats in the congress. 2/13/2022 Section 14. 3 7

Apportionment Problem • The standard quotas represent each state’s exact fair share of the 30 seats for the congress of Margaritaville. – Can state A have 4. 37 seats in congress? • The apportionment problem is to determine a method for rounding standard quota into whole numbers so that the sum of the numbers is the total number of allocated items. – Can we round standard quotas up or down to the nearest whole number and solve this problem? • The lower quota is the standard quota rounded down to the nearest whole number. • The upper quota is the standard quota rounded up to the nearest whole number. 2/13/2022 Section 14. 3 8

Apportionment Problem Example: Here’s the apportionment problem for Margaritaville. There are four different apportionment methods called Hamilton’s method, Jefferson’s method, Adam’s method, and Webster’s method. 2/13/2022 Section 14. 3 9

Hamilton’s Method 1. Calculate each group’s standard quota. 2. Find the lower quota. 3. Give the surplus items, one at a time, to the groups with the largest decimal parts until there are no more surplus items. 2/13/2022 Section 14. 3 10

Hamilton’s Method Example: Consider the lower quotas for Margaritaville. We have a surplus of 1 seat. The surplus seat goes to the state with the greatest decimal part. The greatest decimal part is 0. 38 for state C. Thus, state C receives the additional seat, and is assigned 8 seats in congress. 2/13/2022 Section 14. 3 11

Quota’s Rule • A group’s apportionment should be either its upper quota or its lower quota. An apportionment method that guarantees that this will always occur is said to satisfy the quota rule. • A group’s final apportionment should either be the nearest upper or lower whole number of its standard quota. 2/13/2022 Section 14. 3 12

Jefferson’s Method 1. Find a modifier divisor, d, such that each group’s modified quota is rounded down to the nearest whole number, the sum of the quotas is the number of items to be apportioned. • The modified quotients that are rounded down are called modified lower quotas. 2. Apportion to each group its modified lower quota. 2/13/2022 Section 14. 3 13

Jefferson’s Method Using Jefferson’s Method Example: A rapid transit service operates 130 buses along six routes, A, B, C, D, E, and F. The number of buses assigned to each route is based on the average number of daily passengers per route. Use Jefferson’s method with d = 486 to apportion the buses. Route Average Number of Passengers 2/13/2022 A B C 4360 5130 7080 Section 14. 3 D E F Total 10, 245 15, 535 22650 65, 000 14

Jefferson’s Method Example Continued Solution: Using d = 486, the table below illustrates Jefferson’s method. 2/13/2022 Section 14. 3 15

Adam’s Method 1. Find a modifier divisor, d, such that each group’s modified quota is rounded up to the nearest whole number, the sum of the quotas is the number of items to be apportioned. • The modified quotients that are rounded up are called modified upper quotas. 2. Apportion to each group its modified upper quota. 2/13/2022 Section 14. 3 16

Adam’s Method Using Adam’s Method Example: A rapid transit service operates 130 buses along six routes, A, B, C, D, E, and F. The number of buses assigned to each route is based on the average number of daily passengers per route. Use Adam’s method to apportion the buses. Route Average Number of Passengers 2/13/2022 A B C 4360 5130 7080 Section 14. 3 D E F Total 10, 245 15, 535 22650 65, 000 17

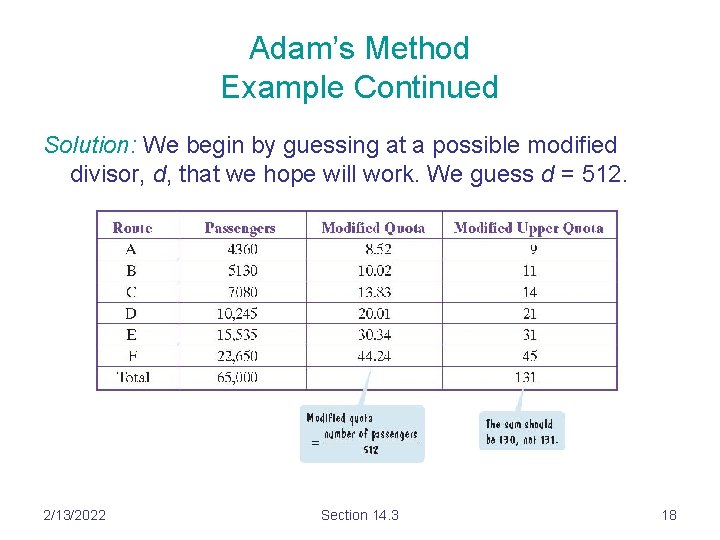
Adam’s Method Example Continued Solution: We begin by guessing at a possible modified divisor, d, that we hope will work. We guess d = 512. 2/13/2022 Section 14. 3 18

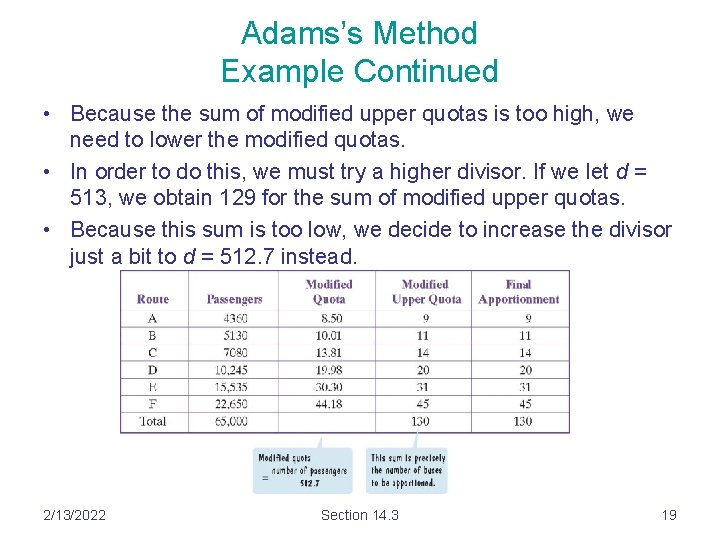
Adams’s Method Example Continued • Because the sum of modified upper quotas is too high, we need to lower the modified quotas. • In order to do this, we must try a higher divisor. If we let d = 513, we obtain 129 for the sum of modified upper quotas. • Because this sum is too low, we decide to increase the divisor just a bit to d = 512. 7 instead. 2/13/2022 Section 14. 3 19

Webster’s Method 1. Find a modifier divisor, d, such that each group’s modified quota is rounded to the nearest whole number, the sum of the quotas is the number of items to be apportioned. • The modified quotients that are rounded down are called modified rounded quotas. 2. Apportion to each group its modified rounded quota. 2/13/2022 Section 14. 3 20

Webster’s Method Using Webster’s Method Example: A rapid transit service operates 130 buses along six routes, A, B, C, D, E, and F. The number of buses assigned to each route is based on the average number of daily passengers per route. Use Webster’s method to apportion the buses. Route Average Number of Passengers 2/13/2022 A B C 4360 5130 7080 Section 14. 3 D E F Total 10, 245 15, 535 22650 65, 000 21

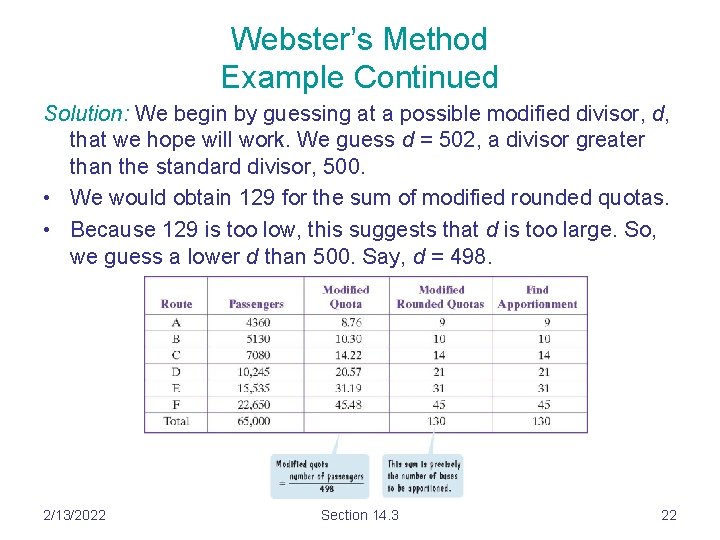
Webster’s Method Example Continued Solution: We begin by guessing at a possible modified divisor, d, that we hope will work. We guess d = 502, a divisor greater than the standard divisor, 500. • We would obtain 129 for the sum of modified rounded quotas. • Because 129 is too low, this suggests that d is too large. So, we guess a lower d than 500. Say, d = 498. 2/13/2022 Section 14. 3 22